군대에서 공부하다가 Dacon 대회에 처음나가 상위 6.3퍼에서 막힌 상태다.
어떻게 하면 남은 12일동안 더 위로 올라갈 수 있을까 생각하다가 12일이 아닌 큰 미래를 보기로 결정했다.
"다시 처음부터"
이 머신러닝 시리즈는 내 인공지능의 Base가 되어준 『파이썬 머신러닝 완벽 가이드 - 권철민』을 다시 곱씹어 읽어보며 작성하려고 한다.
이외에도 필요하거나 따로 공부하면서 알아낸 정보 출처는 reference에 넣어두겠다.
모든 환경설정은 google Colab pro에서 진행되지만 pro가 아니어도 된다.
혹시나 틀린 개념이 있거나 궁금한 점이 있으시면 알려주시면 감사하겠습니다.
머신러닝〔Machine Learning〕
머신러닝이란 단어의 의미를 한 문장으로 표현한다고 하면
"주어진 데이터를 가지고 스스로 학습하는 기계"라고 표현 할 수 있다.
기계가 학습한다는 의미를 가진 이 기술은 기존 개발자들이 하나하나 규칙을 찾고 조건문을 빼곡히 쌓아두는 비효율적인 방식에서 탈피하게 했다.
# 빼곡한 조건문으로 세워진 프로그램.
if A가 들어오면:
if a가 들어오면:
elif a-a가 들어오면:
elif B가 들어오면:
if b가 들어오면:
elif b-b가 들어오면:
elif C가 들어오면:
elif D가 들어오면:
elif E가 들어오면:
.
.
.위처럼 일일이 규칙을 세워두면 예외가 발생했을 때 대처하기 힘들어진다.
이런 상황에서 머신러닝은 Data를 기반으로 Data를 관통하는 규칙을 찾아낸다.
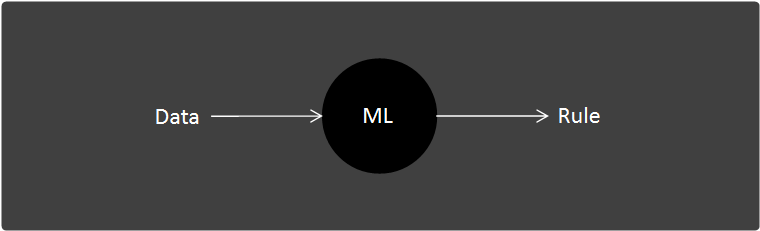
하지만 머신러닝도 단점이 있다.
Data를 가지고 학습하다보니 Data에 의존적이라는 점이다.
"Garbage In Garbage Out"이라는 말처럼 아무리 좋은 알고리즘이라도 쓰레기 Data를 넣으면 쓰레기 Output이 나온다.
즉, 머신러닝의 성능이 좋으려면 좋은 데이터와 좋은 알고리즘 모델이 있어야 한다.
Numpy〔Numerical-Python〕?
머신러닝 모델의 주요 알고리즘은 선형대수와 통계에 기반하는 경우가 많다.
Numpy는 파이썬에서 선형대수 기반의 프로그램을 쉽게 만들 수 있게 해주는 대표적인 패키지다.
대량 Data의 연산을 루프가 아닌 배열을 통해 연산 가능하게 해준다.
이런 이유때문에 파이썬 기반의 많은 머신러닝 패키지는 Numpy에 의존하고 있다.
Numpy는 배열 기반의 연산도 가능케 해주지만 데이터 핸들링 기능도 제공해준다.
하지만 이후에 공부할 Pandas가 존재하기 때문에 적어도 정형 데이터에서는 Pandas를 많이 쓴다.
Coding📄
머신러닝을 하기에 앞서 필수적으로 알아야 할 API를 공부해보자.
- import numpy
import numpy as np꼭 위처럼 import 해줄 필요는 없지만 나름의 관례이니 numpy를 np라고 축약해 작성하는 것을 습관화 하자.
1.ndarray 데이터 타입
- np.array
앞에서 Numpy는 파이썬에서 배열단위로 계산이 가능하게 해준다고 언급했다.
Numpy에서는 np.array를 이용해 ndarray(넘파이 배열)를 만들 수 있다.
머신러닝에서 Input과 Output이 ndarray type인 경우가 많다.
import numpy as np
# np.array로 ndarray 생성.
array1d = np.array([1, 2, 3])
array2d = np.array([[1, 2, 3], [4, 5, 6]])
array2d_1 = np.array([[1, 2, 3]])
# shape확인.
print(array1d.shape)
print(array2d.shape)
print(array2d_1.shape)
=>
(3,)
(2, 3)
(1, 3)위 Output의 결과에서 (3,)와 (1, 3)의 차이가 중요하다.
(3,)는 1차원, (1, 3)은 2차원을 의미한다.
- ndarray.dtype
ndarray를 이용하다보면 Data value의 type을 알고싶을 수 있다.
이때 array객체의 dtype attribute를 이용하면 된다.
print(1d_array.dtype)
=> dtype('int64')이때 ndarray에 여러 type의 value가 들어갈 수 있는데 이 경우에 dtype을 이용하면 데이터 용량이 더 큰 값을 나타낸다.
array1d_multiple = np.array(['1', 2, 3])
print(array1d_multiple.dtype)
=> dtype('<U21')- ndarray.astype()
Numpy에서는 이런 data type을 바꿔주는 역할인 astype()메소드가 있다.
ndarray의 astype()를 이용하면 원하는 type으로 value를 바꿔줄 수 있다.
큰 Data를 다루는 프로젝트중 메모리를 절약해야 할 때 이용된다.
# 기존의 int64형을 str로 변형
array1d = array1d.astype('str')
print(array1d.dtype)
=> dtype('<U1')2.ndarray 생성/변경
- arange, zeros, ones
np.arange()는 ndarray를 start부터 end -1까지 step단위로 만들어준다.
np.arange(0, 10)
=> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.arange(1, 10)
=> array([1, 2, 3, 4, 5, 6, 7, 8, 9])
np.arange(1, 10, 2)
=> array([1, 3, 5, 7, 9])np.zeros는 0으로 채워진 ndarray를 만들어준다.
np.zeros((4, 5))
=>
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])np.ones는 1로 채워진 ndarray를 만들어준다.
np.ones((4, 5))
=>
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
np.zeros와 np.ones의 인자에는 ndarray value type을 정할 수 있는 인자가 있다.
위는 float형으로 만들어졌는데 아래와 같이 int형으로 바꿀 수도 있다.
np.ones((4, 5), dtype='int')
=>
array([[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]])- ndarray.reshape()
인공지능을 하다보면 Model에 따라 Data를 형 변환해야하는 경우가 생길 수 있다.
이때 Numpy는 ndarray.reshape() 메소드를 제공해 형 변환을 가능하게 해준다.
# 9개 값을 가진 1차원 ndarray 생성.
array1d = np.arange(9)
# (3, 3)으로 reshape
array1d.reshape((3, 3))
=>
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
# (9, 1)로 reshape
array1d.reshape((9, 1))
=>
array([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8]])
# (3, 3)으로 reshape
array1d.reshape((3, -1))
=>
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
위 코드를 보면 어떤 식으로 사용할 지 감이 잡힐 것이다.
여기서 중요하게 짚고 넘어가야 할 부분이 있다.
array1d.reshape(3, -1)은 처음 Numpy를 공부하는 사람이라면 어색할 수 있다.
-1에 대해 간단하게 설명하자면 파이썬에게 "나는 이 데이터를 어떤 형식으로 바꾸고 싶은데 너가 유추해서 바꿔봐."라고 말하는 것과 같다.
array1d.reshape(3, -1)이라는 말은 "나는 array1d를 (3, ?)형식으로 바꾸고 싶은데 너가 유추해서 바꿔봐."라고 하는 것과 같다.
Data의 개수 9개에서 3을 나눠 9/3=3 => (3, 3)이라는 계산을 하는 형식이다.
reshape는 실제 머신러닝에서 데이터 차원을 바꾸거나 행렬을 바꿀 때 많이 사용되므로 꼭 이해하도록 하자. 특히, 머신러닝에서 reshape를 이용해 차원을 바꾸는 경우에 사용하는 '-1'에 대한 개념은 중요하다.
3.ndarray 인덱싱(Indexing)
머신러닝을 하다보면 특정 값을 가져와야 하는 경우가 있다.
이를 위해 Numpy ndarray에는 인덱싱(indexing)이라는 기법이 있다.
인덱싱을 공부하기 전에 Data에 인덱스가 어떻게 새겨지는지 확인해보자.
- Data 인덱스
인덱스는 Data의 주소 역할을 해주는 고유한 값이다.
쉽고 빠르게 Data를 찾아주는 역할을 한다고 보면 된다.
그림으로 이해해보자.
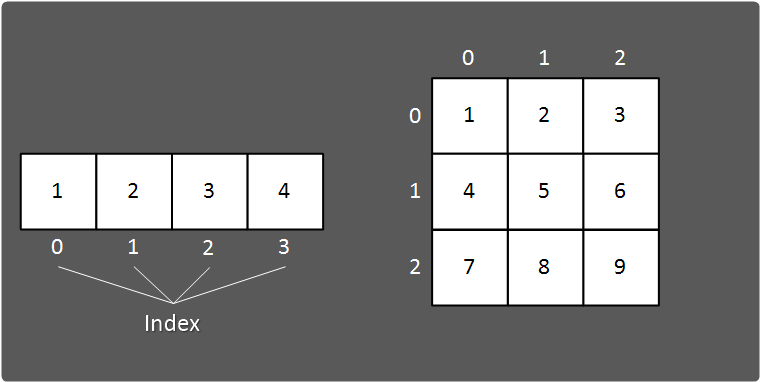
각각 왼쪽은 1차원 오른쪽은 2차원 배열을 그림으로 표현했다.
인덱스는 0부터 시작한다.
2차원 이상의 다차원 배열에 대해 처음부터 너무 이해하려고 하지 않는게 좋은 것 같다.
일단 머신러닝에서는 2차원 Data를 다루는 경우가 많으므로 행과 열의 개념으로 Data가 존재한다고 생각하면 좋을 것 같다.
이 장의 마지막에 차원에 대해 자세히 적었으니 참고해주면 좋을 것 같다.
- 단일 값 추출
ndarray에서는 특정 Data를 추출하는 단일 값 추출이라는 방법이 있다.
이는 말 그대로 Data 1개의 값을 추출할 때 사용된다.
# ndarray 생성.
array1d = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
print(array1d[1])
=> 2
print(array1d[-1]
=> 9위처럼 1차원 데이터에서는 '[ ]'안에 추출하고자 하는 인덱스 하나를 입력해주면 된다.
ndarray에서 '[]'의 의미는 인덱싱을 하겠다는 의미다. 모든 인덱싱에서 공통이다.
2차원 데이터는 다음과 같이 인덱싱 할 수 있다.
# 2차원 ndarray 생성.
array2d = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(array2d[1, 1])
=> 5- 슬라이싱
단일 추출을 하면 하나의 Value를 추출하기엔 편리하지만 한번에 여러 데이터를 추출하고 싶은 경우에는 루프(loop)를 돌려야 하는 번거로움이 있다.
슬라이싱을 이용하면 이런 번거로움을 줄일 수 있다.
'[ ]'안에 ':'를 이용해 슬라이싱을 할 수 있는데 다음과 같다.
ndarray[a:b]라는 의미는 "ndarray의 a인덱스부터 b-1인덱스까지를 불러와줘."라는 의미가 된다.
# ndarray 생성.
array1d = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
# 슬라이싱
print(array1d[1:3])
=> [2 3]
# 2차원 ndarray 생성.
array2d = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 슬라이싱
print(array2d[1:3, 1:3])
=>
[[5 6]
[8 9]]위 코드에서 2차원 ndarray slicing 의미는 "1~2까지의 행이면서 1~2까지의 열인 값을 추출해줘."이다.
- 팬시 인덱싱
팬시 인덱싱은 ndarray에 존재하는 Data를 더 유연하게 추출할 수 있도록 해준다.
'[ ]'안에 리스트나 ndarray를 넣어 원하는 데이터를 추출할 수 있게 해준다.
# 1차원 ndarray 생성.
array1d = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
# 팬시 인덱싱
print(array1d[[1, 3, 4]])
=> [2 4 5]
# 2차원 ndarray 생성.
array2d = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 팬시 인덱싱
print(array2d[[0, 2], [2]])
=> [3 9]- 불린 인덱싱
불린 인덱싱은 머신러닝에서 많이 쓰이는 인덱싱 기법이다.
불린 인덱싱은 한번에 조건 필터링과 추출을 동시에 할 수 있기 때문이다.
# 2차원 ndarray 생성.
array2d = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(array2d[array2d > 5])
=> [6 7 8 9]위는 ndarray에서 Data가 5를 초과하는 경우의 Data를 추출하는 것이다.
array2d > 5라는 조건식을 뽑으면 다음과 같다.
array2d > 5
=>
array([[False, False, False],
[False, False, True],
[ True, True, True]])즉, ndarray '[ ]'에는 위와 같은 불린 값이 들어가게 된다.
이때 True인 값의 인덱스를 반환하게 되고 그로인해 ndarray는 값을 추출해낸다.
# 2차원 조건
cond1 = [[False, False, False],
[False, False, True],
[True, True, True]]
print(array2d[cond1])
=> [6 7 8 9]4.ndarray 정렬
Numpy에서 ndarray를 정렬하는 방법에 대해 알아보자.
- ndarray.sort( ), np.sort( )
정렬은 ndarray.sort( )처럼 행렬에서 sort하는 방법과 np.sort( )처럼 Numpy에서 sort하는 방법이 있다.
둘의 차이는 원본 행렬이 유지가 되냐 안되냐 차이이다.
행렬에서 sort를 호출하면 원본 행렬이 바뀌고, Numpy에서 sort를 호출하면 원본 행렬은 그대로다.
array1 = np.array([1, 3, 2, 8, 9])
array1.sort()
print('변환된 행렬:', array1)
print('원본 행렬:', array1)
=>
변환된 행렬: [1 2 3 8 9]
원본 행렬: [1 2 3 8 9]array1 = np.array([1, 3, 2, 8, 9])
print('변환된 행렬:', np.sort(array1))
print('원본 행렬:', array1)
=>
변환된 행렬: [1 2 3 8 9]
원본 행렬: [1 3 2 8 9]default는 오름차순으로 정렬이고 내림차순으로 정렬하고싶으면 함수 뒤에 [::-1]을 붙이면 된다.
array1 = np.array([1, 3, 2, 8, 9])
array1.sort()
array1 = array1[::-1]
print('변환된 행렬:', array1)
print('원본 행렬:', array1)
=>
변환된 행렬: [9 8 3 2 1]
원본 행렬: [9 8 3 2 1]array1 = np.array([1, 3, 2, 8, 9])
print('변환된 행렬:', np.sort(array1)[::-1])
print('원본 행렬:', array1)
=>
변환된 행렬: [9 8 3 2 1]
원본 행렬: [1 3 2 8 9]배열이 2차원이면 axis축 인자를 통해 정렬하고자 하는 기준을 정할 수 있다.
axis=0은 행, axis=1은 열 이라고 생각해도 좋다.
array2 = np.array([[1, 12, 3],
[7, 2, 4]])
array2_row = np.sort(array2, axis=0)
print(array2_row)
=>
[[ 1 2 3]
[ 7 12 4]]위는 행 기준으로 정렬한 것이다.
array2 = np.array([[1, 12, 3],
[7, 2, 4]])
array2_col = np.sort(array2, axis=1)
print(array2_col)
=>
[[ 1 3 12]
[ 2 4 7]]위는 열 기준으로 정렬한 것이다.
- np.argsort( )
Numpy에는 argsort라는 함수가 있는데 이는 정렬한 값을 반환하는 것이 아니라 정렬한 값의 원래 인덱스를 반환하는 것이다.
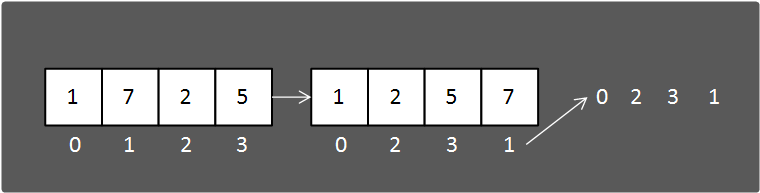
위 그림을 보면 이해하기 쉬울 것이다.
array1 = np.array([1, 7, 2, 5])
print(np.argsort(array1))
=> [0 2 3 1]np.argsort( )함수도 axis를 이용하여 2차원 데이터를 정렬할 수 있다.
5.선형대수 연산
처음 Numpy에 대해 설명할 때 파이썬에서 선형대수 기반의 프로그램을 쉽게 만들 수 있게 해주는 대표적인 패키지라고 했다.
이번에는 Numpy로 선형대수 연산을 어떻게 진행하는지 알아보자.
머신러닝에서 많이 쓰이는 선형대수 연산인 '행렬 내적'과 '전치 행렬'에 대해 알아보겠다.
- 행렬 내적(np.dot( ))
array1 = np.array([[1, 2, 3],
[2, 3, 1]])
array2 = np.array([[2, 1],
[1, 2],
[2, 2]])
# 행렬 내적
print(np.dot(array1, array2))
=>
[[10 11]
[ 9 10]]내적에 대해 자세히 설명하지는 않겠지만 아래와 같은 로직이다.
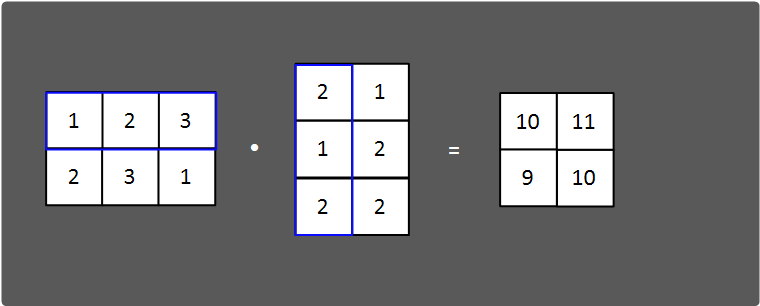
- 전치 행렬(np.transpose( ))
원 행렬에서 행과 열 위치를 교환한 행렬을 원 행렬의 전치 행렬이라고 한다.
Numpy에서는 np.transpose( )함수를 이용해 이를 지원한다.
array1 = np.array([[1, 2, 3],
[2, 3, 1]])
array1_t = np.transpose(array1)
print(array1_t)
=>
[[1 2]
[2 3]
[3 1]]차원(dimension)
마지막으로 차원에 대해 알아보자.
Data의 차원이라 하면 너무 거창하게 생각할 필요 없다.
우리가 흔히 말하는 '1차원 리스트'는 1차원, '2차원 리스트'는 2차원 ... 이라고 생각하면 된다.
차원을 구성하는 요소는 axis가 있다.
1차원 배열은 axis=0으로 되어있고, 2차원 배열은 axis=0, axis=1로 되어있다.
즉, axis=n, axis=n-1, axis=n-2, axis=n-3 ...은 가장 바깥쪽 리스트를 기준으로 0부터 이름 붙인 것이다.
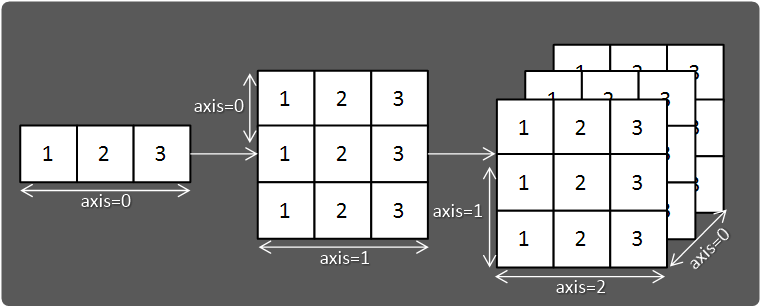
정확히 맞는 말인진 모르겠지만 내가 공부할 때는 axis=n에서 n이 커질수록 차원은 저차원으로 간다고 이해했다.(4차원 이상으로 가면 행과 열, 높이같은 직관적인 이해는 거의 불가능하기 때문이다.)
지금 이를 이해하기 어렵다면 우선 2차원 데이터에서 axis=0 축은 행을 의미하고, axis=1 축은 열을 의미한다고 생각하면 된다.

