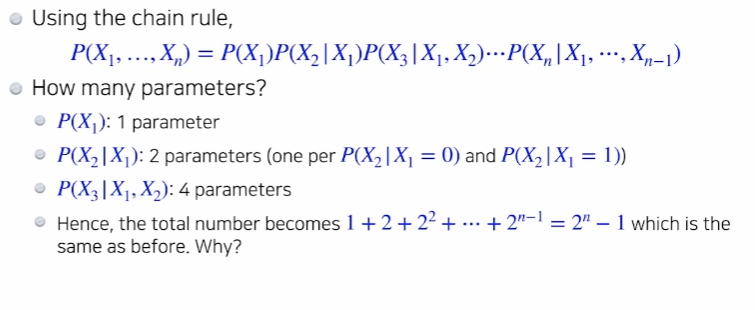Generative Model

Learning a Generative Model

• Generative model은 input에 대한 distribution(분포)을 학습한다.

Basic Discrete Distributions

• Bernoulli distribution(베르누이 확률변수) : 확률이 0 아니면 1인 변수. ex) 동전 던지기

  $X \sim Ber(p)$

• Categorical distribution(카테고리 분포) : 1부터 k까지의 k 개의 정수 값 중 하나가 나오는 확률변수의 분포 ex) 주사위 던지기

  $Y \sim Cat(p_1,...,p_m)$

• RGB 이미지의 픽셀 하나가 갖는 경우의 수는 $256 \times256 \times256$이다.
• 한개의 픽셀의 확률분포를 완벽하게 표현하기 위한 파라미터의 수는 $256 \times256 \times256-1$개 이다.(확률의 합은 1이므로 $256^3-1$의 개수만 알면 나머지 하나는 알 수있다.)

• mnist와 같은 간단한 이미지도 엄청나게 많은 파라미터가 필요한 것을 볼 수 있다.

Structure Through Independence

• 이 분포를 표현할 수 있는 파라미터의 수는 n?
  각각의 픽셀이 가질 수 있는 경우의 수는 2개
  우리가 가질 수 있는 경우의 수가 n개일때 n개를 표현 할 수 있는 파라미터의 수는 n-1
  즉, 784개의 픽셀들이 있기 때문에 n개의 혹은 784개의 파라미터만 있으면 binary 이미지를 표현 할 수 있다.

우리가 가지고 있는 binary이미지의 경우의수는 2^n으로 여전히 동일하지만 이 확률분포를 표현하기 위한 파라미터의 숫자는 2^n-1라는 큰 숫자에서 n이라는 작은 숫자로 줄어들었다.
이러한 independence assumption -> 우리가 표현할 수 있는 표현력을 굉장히 줄여버린다.

Conditional Independence

Autoregressive Models

-

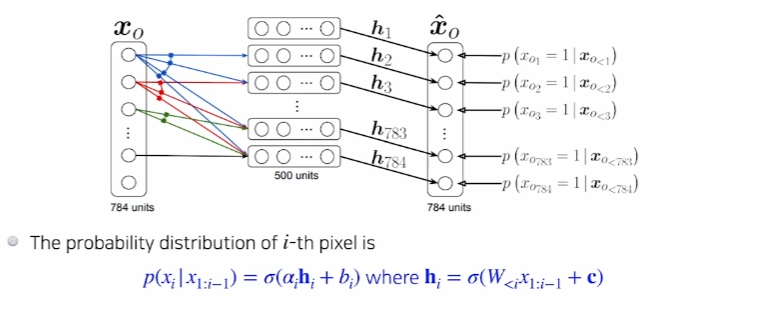
NADE : Neural Autoregressive Density Estimator

• explicit : 단순히 무언가를 생성할 수 있을 뿐만 아니라 새로운 입력이 주어졌을때 그 입력(이미지)이 얼마나 우리가 모델링하는것에 likely한지를 뜻함

Summary of Autoregressive Models