SASRec: Self-Attentive Sequential Recommendation
한줄요약
SASRec이라는 Self-Attention based로 하는 Sequential Recommendation에 관한 논문이다.
ABSTRACT
Markov Chains (MCs) -> 보통 마지막 interaction만 보니깐 sparse에 강하지만 마지막 interaction만 참고하는게 약점이 될 수 있음
Recurrent Neural Networks (RNNs) -> 장기적인 의미 발견 가능하지만 dense한 데이터셋에만 강하다는 약점이 있음
Self-Attention based Sequential Model (SASRec) -> MCs와 RNNs의 두 가지 목표를 균형 있게 맞춤. Self-Attention을 활용한다는 것이 가장 큰 contribution.
I. INTRODUCTION
sequential recommendation -> high-order dynamics을 간결하게 포착하는 방법에 중점을 둔다.
MCs -> sparse한 데이터에서 잘 작동하지만 복잡한 시나리오는 capture하기 힘들다.
RNNs -> 표현력은 뛰어나지만 dense한 데이터가 있어야 잘 작동한다는 단점이 있다.
이 2가지 방법의 문제점을 해결하기 위해 이 논문에서 제안하는 것이 NLP 분야의 Transfomer를 가져오는 것이다. Transfomer는 self-attention이라는 mechanism을 사용한다. 이것은 문장 내 단어들 사이의 syntactic, semantic pattenrs를 발견하는데 효율적이다. 여기에 영감을 받아서 Self-Attention based Sequential Recommendation model (SASRec)을 구축한다.
SASRec은 MC/CNN/RNN-based sequential recommendation methods를 능가한다. SASRec은 dense한 데이터셋은 long-range dependencies를 고려하는 경향을 보이고, sparse한 데이터셋은 최근 활동에 집중하는 모습을 보인다. 이는 SASRec 다양한 density의 데이터셋을 적응적으로 처리한다고 볼 수 있다 (Section 4 참고).
SASRec의 핵심 구성 요소인 self-attention block은 parallel acceleration에 적합하여 CNN/RNN 기반의 모델보다 더 빠르게 작동한다.
II. RELATED WORK
A. General Recommendation
B. Temporal Recommendation -> 순서만을 고려하는 Sequential Recommendation과 다르게 시간적 패턴까지 고려한다.
C. Sequential Recommendation -> MCs, RNNs
D. Attention Mechanisms -> NLP에서 활용하는 그대로 가져와서는 안 되고 sequential recommendation에 맞게 특별히 설계된 모델이 필요하다.
III. METHODOLOGY
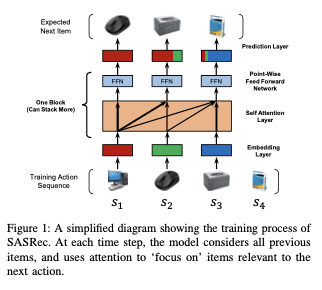
위의 Figure 1처럼 sequential recommendation은 s1 s2 s3가 순서대로 있으면 s4를 예측하는 것이다.
이번 Section 3에서는 embedding layer, several self-attention blocks, prediction layer를 통해 모델을 구축하는 방법을 소개한다.

A. Embedding Layer
첫번째로 training sequence를 fixed-length sequence로 만든다. 논문에서는 maximum sequence length를 n으로 정의한다. 만약 sequence length가 n보다 길면 가장 최근 n개를 가져오고, n보다 짧으면 앞에는 padding으로 0을 채운다.
input embedding matrix E는 item embedding matrix M과 position embedding P의 합으로 아래와 같이 나타내진다.
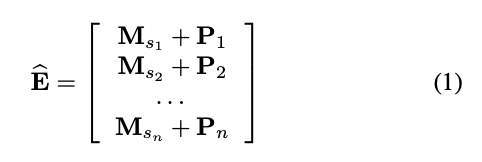
B. Self-Attention Block
Transfomer에서 나오는 self-attention은 아래와 같이 표현된다 (혹시 모른다면 transfomer 논문 참고).
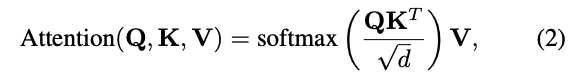
이 논문에서는 Q (aueries), K (keys) , V (values)를 linear projections하여 3개의 행렬로 변환하고 이것을 attention layer에 전달한다. WQ, WK, WV는 projection matrices이다. projections은 모델을 더 flexible하게 한다 (예를 들어 <query i, key j> != <query j, key i>). 수식은 아래와 같다.
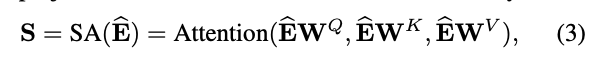
여기서 예를 들어 (t+1)번째 item을 예측할 때는 t번째까지의 item만을 고려해야한다. 그렇기 때문에 수식 (2)에서 attention 수식을 계산할 때 Q와 K를 연산할 때 Qi와 Kj의 관계에서 j > i 라는 조건이 걸려있어야한다 (이 조건이 안 걸려 있으면 그 이후에 item을 알려주는 꼴이 되어버림). 그래서 Q와 K를 연산한 후에 0으로의 masking 작업이 필요하다. 그 이후에 V와의 연산을 수행하면 된다.
직관적으로 Q와 K의 연산을 통해 item 간의 상관관계를 파악할 수 있고, V와의 연산을 통해 item 간의 상관관계가 반영된 sequence embedding을 구해낼 수 있다.
여기까지의 연산은 linear model이다. 이 논문을 떠나서 딥러닝이 크게 성공할 수 있었던 가장 큰 이유 중에 하나는 non-linear funtiond을 통해서 모델을 non-linear하게 만들었기 때문이다. 여기서도 마찬가지로 모델에 nonlinearity을 부여하고 다양한 latent dimensions간의 interactions를 고려하기 위해 모든 Si에 대하여 동일하게 point-wise feed-forward network를 적용한다 (parameters는 공유). 더 자세히 말하면 모든 Si를 독립적으로 각각 FFN을 하는 것이다. 다시 말해 Si와 Sj간의 interaction은 전혀 없다. 이는 information leaks (정보가 뒤에서 앞으로 새는 것)를 방지한다는 의미이다. 수식은 아래와 같다.
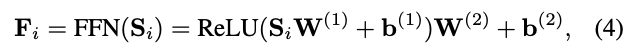
C. Stacking Self-Attention Blocks
위에까지의 수식으로 first self-attention block 이후의 Fi는 본질적으로 모든 이전 item들의 embeddings를 aggregates한다. 여기서 더 complex하게 하기 위해서 self-attention block을 F 기반으로 쌓는 것이 유용할 수 있다. 구체적으로 self-attention block (self-attention layer, feed-forward network)을 쌓는다. b번째 (b > 1) block은 아래 수식과 같이 정의한다.
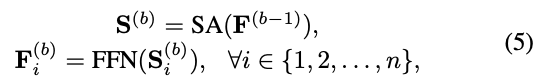
그리고 b = 1 번째 block은 아래 수식과 같이 정의한다.
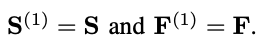
그러나 network가 깊어질수록 overfitting, vanishing gradients, more training time과 같은 문제점들이 발생한다. 이를 해결하기 위해 아래와 같은 수식을 추가한다. g(x)는 self-attention layer 또는 feed-forward network를 나타낸다. 각 block의 layer g에 대하여 input x에 layer normaliztion을 적용한 후 g에 넣고 그 output을 dropout에 적용한 다음에 final output에 x를 더한다.
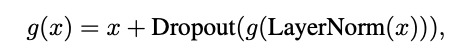
이 수식과 관련해 좋은 그림이 있어 가져와본다 (출처: https://www.youtube.com/watch?v=PKYVHGrSO2U).
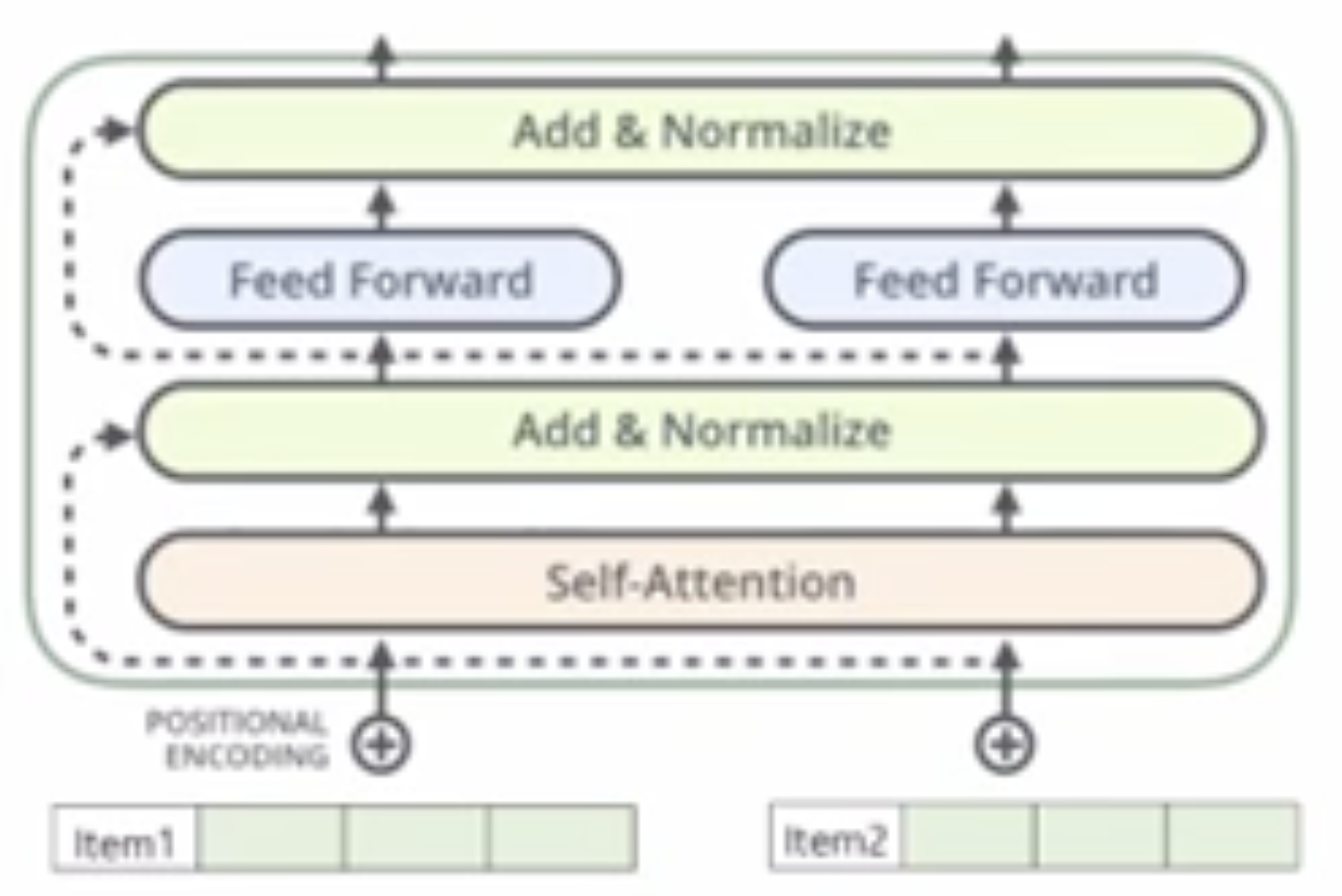
여기서 Residual Connections, Layer Normalization, Dropout의 3가지의 방법을 사용한다.
Residual Connections -> 당연하게도 마지막으로 방문한 item이 sequential recommenation에서 가장 중요하다. residual connections이 없다면 마지막으로 방문한 item이 그 이전 item들과 섞여버리게 되는데 마지막으로 방문한 item의 embedding을 final layer으로 propagate하는 residual connections을 추가하면 모델이 low-layer information을 활용하는게 훨씬 쉬어진다.
Layer Normalization -> 훈련을 안정화하고 가속화하는데 유용하다.
Dropout -> overfitting 문제를 완화해준다.
D. Prediction Layer
아래의 수식과 같이 계산되어 최종 예측 값을 뱉어낸다.

E. Network Training
loss function은 아래와 같이 BCE loss를 사용하여 모델을 최적화 한다.

F. Complexity Analysis
(논문 참고)
G. Discussion
(논문 참고)
IV. EXPERIMENTS
RQ1: Does SASRec outperform state-of-the-art models including CNN/RNN based methods?
RQ2: What is the influence of various components in the SASRec architecture?
RQ3: What is the training efficiency and scalability (regard- ing n) of SASRec?
RQ4: Are the attention weights able to learn meaningful patterns related to positions or items’ attributes?
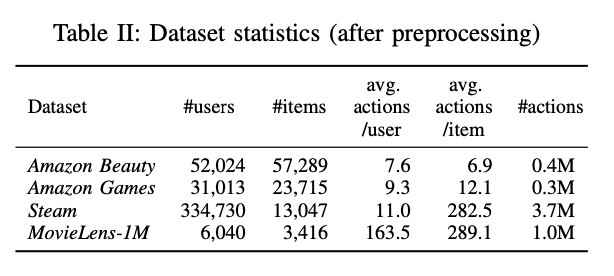
A. Datasets
dataset의 train-validation-test를 split하는 방법은 가장 최근 action이 test set, 두번째로 최근 action이 validation set, 나머지 모든 action은 test set이다.
예를 들어 s1, s2, s3, s4, s5가 있다면
s1, s2, s3가 train set
s4가 validation set
s5가 test set이다.
B. Comparison Methods
- PopRec
- Bayesian Personalized Ranking (BPR)
- Factorized Markov Chains (FMC)
- Factorized Personalized Markov Chains (FPMC)
- Translation-based Recommendation (TransRec)
- GRU4Rec
- GRU4Rec+
- Convolutional Sequence Embeddings (Caser)
C. Implementation Details
(논문 참고)
D. Evaluation Metrics
Hit Rate@10, NDCG@10를 사용한다.
E. Recommendation Performance
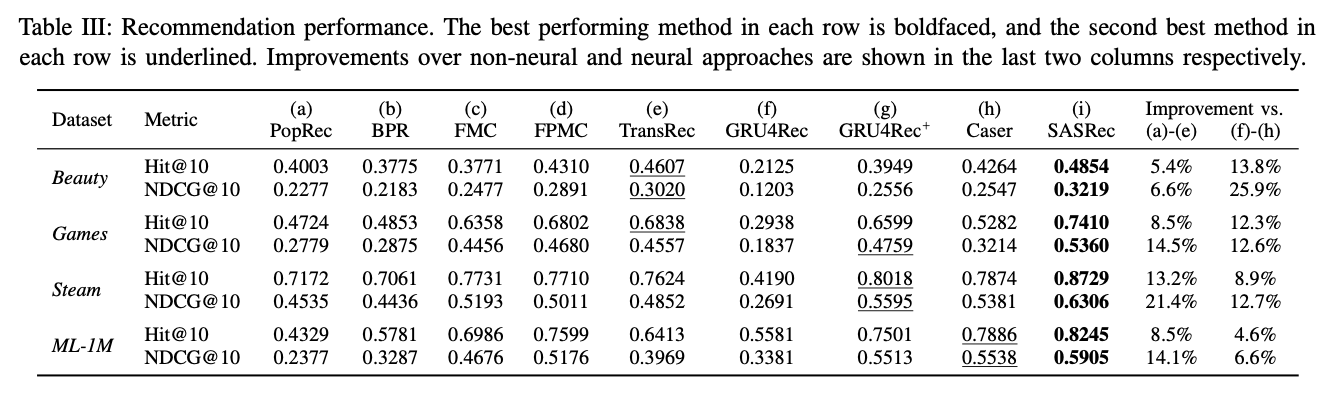
F. Ablation Study
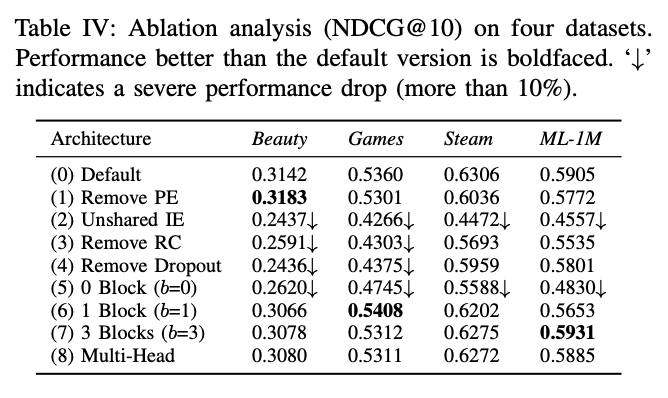
G. Training Efficiency & Scalability
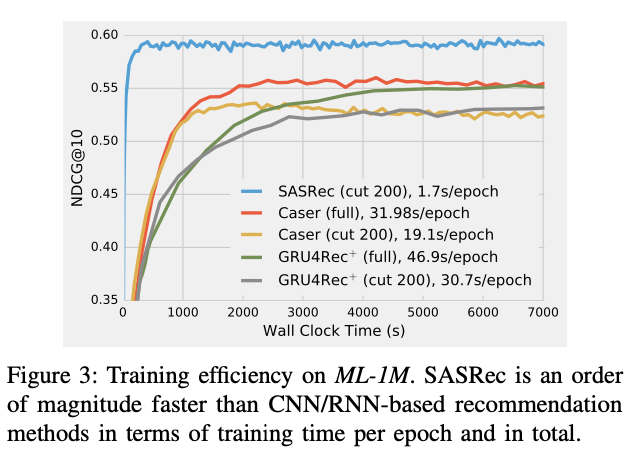
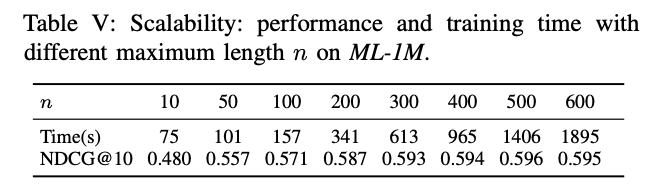
H. Visualizing Attention Weights
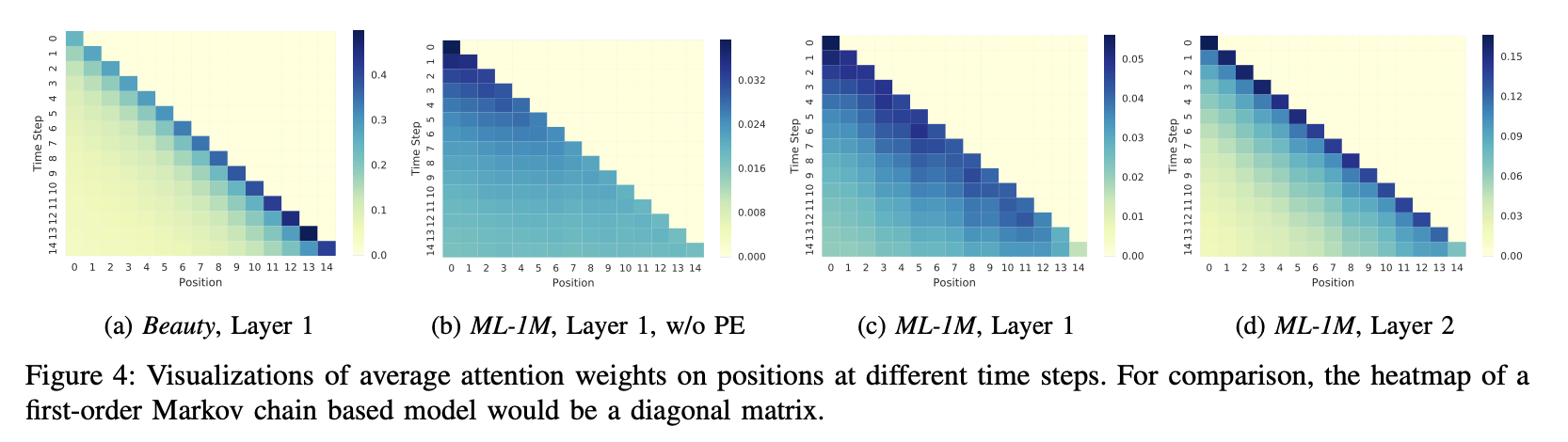
(a) vs (c) -> sparse한 Beauty dataset은 더 최근의 item에 주의를 기울이는 경향이 있고, dense한 ML-1M dataset에서는 덜 최근의 아이템에도 주의를 기울이는 경향이 있다. 이것을 통해 알 수 있는 것은 SASRec이 spase, dense dataset에 맞게 적응적으로 처리되는 것을 보인다는 것이다.
(b) vs (c) -> Position Embeddings (PE)의 효과를 보기에 적합한 비교이다. (b)는 균등하게 분포되는 반면에 (c)는 위치에 더 민감하여 최근 아이템에 더 주의를 기울이는 경향이 있다.
(c) vs (d) -> SASRec은 계층적이기 때문에 서로 다른 block간의 attention이 어떻게 다른지를 볼 수 있다. first self-attention block (c)는 모든 이전 item들을 고려하고, second self-attention block (d)는 첫번째 block에서 이미 모든 이전 item들을 고려했기 때문에 더 먼 위치를 고려할 필요가 없어서 비교적 최근의 item들만 고려된다.
V. CONCLUSION
SASRec은 전체 user sequence를 모델링하고, item을 적응적으로 고려한다. SOTA이며 CNN/RNN 기반 접근법보다 한 차원 더 빠르다.