[인사이드 머신러닝] 대표적인 규제(Regularization)기법들 (Ridge, Lasso, Elastic-Net)

cleansky·2021년 8월 31일

Elastic-Net ElasticNet LASSO regression Lasso Linear Regression MSE contour Regularization Ridge Ridge Regression cleansky diagonal loading 규제 기계학습 머신러닝 선형회귀 인공지능 인사이드 머신러닝 정규화

인사이드 머신러닝

목록 보기

8/12

규제(Regularization)란 무엇인가?

우리 말로 정규화라고도 불린다. 그렇지만 나는 개인적으로 규제라고 번역되는 것이 더 자연스럽다고 생각한다. 그래서 여기서는 우리말로는 규제라고 번역한다. 독립변수의 수가 지나치게 많거나 변수간 다중공선성이 크다고 여겨질 때, 회귀 모델의 적합 성능을 향상시키기 위해 변수 선택이나 차원 축소 등의 방법을 사용할 수 있는데, 여기서 한 가지 더 선택할 수 있는 옵션이 바로 규제(Regularization) 방법이다. 이 방법은 회귀계수를 구할 때, 회귀 계수의 크기에 제약을 두어 설명력이 낮은 독립변수에 대한 가중치를 줄인다.

예를 들어, 다음과 같은 $m$ 차 다항회귀모델을 생각해보자.

\tag{1} y = \beta_0 + \beta_1x + \beta_2 x^2 + \dots + \beta_m x^m + \epsilon

아래의 [그림 1] 같은 데이터가 주어졌을 때, 단순회귀모델을 사용하여 1차 회귀직선을 그리게 되면 어느 정도 적합은 되었지만 일부 데이터 포인트들에서 편차가 증가한다. 반면, 식 (1)을 이용하여 아주 고차식으로 회귀선을 적합하게 되면 [그림 1]의 우측 그림과 같이 훈련 데이터에서는 오차가 거의 없는 회귀선을 찾을 수 있게 되겠지만, 훈련데이터와 조금만 다른 데이터가 주어지면 오차가 큰 결과를 출력할 여지가 있다. (다항회귀모델 에서 언급한 것처럼 회귀계수의 분산이 커짐을 의미한다.) 머신러닝에서 전자의 경우를 과소적합(underfitting, 언더피팅) 이라 부르며, 후자를 과대적합(overfitting, 오버피팅) 이라 부른다.

[그림 1] 고차항과 회귀선

[그림 1]과 같이 다항회귀(polynomial regression) 문제에서는 데이터의 scatterplot을 통해 회귀모델의 차수를 선택할 수도 있을 것이다. 그러나 독립변수가 두 개 이상인 다중회귀(multiple linear regression) 모델에서는 이러한 작업이 사실상 불가능하다. 우리는 신뢰성 있는 회귀모델을 얻기 위해 오버피팅과 언더피팅을 완벽하게 회피하고 싶지만 모든 머신러닝 문제는 오버피팅과 언더피팅에서 완전히 자유로울 수 없다. 그러나 어느 정도의 적절한 해결책은 갖고 있는데 그 중 회귀모델에서 널리 사용되는 방법이 바로 규제(Regularization)라는 방법이다.

규제는 회귀계수를 추정하기 위한 최적화 식에 회귀 계수의 크기에 대한 제약식을 추가하는 것을 의미한다. 원리는 이렇다.

언더피팅을 피하기 위해 고차 회귀 모델을 세운다. 여기서 고차란, 다항회귀 모델에서 독립변수의 고차항을 포함하는 것을 의미하기도 하고, 동시에 다중회귀 모델에서 독립변수의 수가 많은 것을 의미하기도 한다1. (좌우지간 고려해야할 변수가 많은 것)
모델의 차원을 높였기 때문에 언더피팅의 가능성은 감소하였지만 반대로 오버피팅의 우려가 있다.
오버피팅이 발생하면 훈련 데이터에만 잘 맞도록 학습되므로 훈련 데이터가 조금만 바뀌더라도 학습 결과가 크게 바뀔 수 있다.
즉, 회귀 계수의 분산이 커지게 된다. 회귀 계수의 분산이 커진다는 것은 회귀 계수의 값이 매우 커질 수 있음을 의미한다.
반대로 회귀 계수의 값이 매우 커지는 것을 방지하면 회귀 계수의 분산이 작아지므로 오버피팅을 방지할 수 있게 된다.
설명력이 부족한 독립변수에 대한 회귀계수의 크기를 효과적으로 억압하는 것은 변수선택에 의해 차원을 축소한 것과 같은 효과를 얻을 수 있기 때문에 오버피팅이 줄어든다고 해석할 수도 있다.

본 포스트에서는 대표적인 규제 기법인 Rigde, Lasso, Elestic-Net regression에 대하여 간략히 살펴보기로 한다.

MSE Contour

본격적으로 규제 방법에 대해 알아보기에 앞서 MSE contour에 대하여 간략하게 짚고 넘어가자. MSE contour란 (2차원 평면의 경우) 동일한 MSE를 갖는 점들을 연결한 선으로 그 개념은 등고선과 같다. 우리는 MSE contour가 수학적으로 어떻게 표현되는지 알아 본 후 그 개념을 여러 규제 방법들에 적용하여 규제 방법들이 어떠한 특성들이 있는지 살펴볼 것이다. 아래의 내용은 고려대학교 김성범 교수님 강의를 참고하였다 [2]. 시각화의 편의를 위해 독립변수가 2개인 경우의 MSE는 다음과 같이 나타낼 수 있다. (실제 아래 식은 SSE이다. 그러나 MSE는 SSE를 상수로 나눈 것에 불과하므로 최적화 관점에서 둘의 차이는 없다.)

\tag{2} \begin{aligned} MSE(\beta_1, \beta_2) &= \sum_{i=1}^N(y_i - \beta_1 x_{i1} -\beta2 x_{i2})^2 \\ &= \sum_{i=1}^N y_i^2 - 2\sum_{i=1}^N y_i(\beta_1 x_{i1} + \beta_2 x_{i2}) + \sum_{i=1}^N(\beta_1 x_{i1} + \beta_2 x_{i2})^2 \\ &= \sum_{i=1}^N y_i^2 - 2\left(\sum_{i=1}^N y_i x_{i1}\right)\beta_1 - 2\left(\sum_{i=1}^N y_i x_{i2}\right)\beta_2 \\ & \ \ + \sum_{i=1}^N \left(\beta_1^2 x_{i1}^2 + \beta_2^2 x_{i2}^2 + 2\beta_1\beta_2 x_{i1} x_{i2}\right) \\ &= \left(\sum_{i=1}^N x_{i1}^2 \right)\beta_{1}^2 + \left(\sum_{i=1}^N x_{i2}^2 \right)\beta_{2}^2 + \left(2\sum_{i=1}^N x_{i1} x_{i2} \right)\beta_1 \beta_2 \\ & \ \ - 2\left(\sum_{i=1}^N y_i x_{i1}\right)\beta_{1} - 2\left(\sum_{i=1}^N y_i x_{i2}\right)\beta_{2} + \sum_{i=1}^N y_i^2 \\ &= A \beta_1^2 + B \beta_1 \beta_2 + C \beta_2^2 + D \beta_1 + E \beta_2 + F \end{aligned}

식 (2)의 마지막 줄은 2차원에서의 conic equation과 같다 [2-3]. 즉, $x$ 축이 $\beta_1$ 이고 $y$ 축이 $\beta_2$ 이며 $z$ 축이 $MSE(\beta_1, \beta_2)$ 인 3차원 좌표계에서 $MSE(\beta_1, \beta_2)$ 는 원뿔과 같은 형태를 띄게 되며, 동일한 값의 $MSE(\beta_1, \beta_2)$ 를 갖는 $(\beta_1, \beta_2)$ 를 MSE contour로 [그림 2]와 같이 시각화 할 수 있다. (아래 그림은 $(\beta_1, \beta_2)$ 대신 $(x_1, x_2)$ 로 표기되어 있다.)

[그림 2] MSE Contour 시각화 결과 (source: [4])

참고로 $A \beta_1^2 + B \beta_1 \beta_2 + C \beta_2^2 + D \beta_1 + E \beta_2 + F = 0$ 의 판별식(discriminant of conin equation) $B^2-4AC$ 에 의해 MSE contour (원뿔의 단면)은 다음과 같은 형태를 갖는다.

$B^2-4AC = 0$ $\rightarrow$ parabola (포물선)
$B^2-4AC > 0$ $\rightarrow$ hyperbola (쌍곡선)
$B^2-4AC < 0$ $\rightarrow$ ellipse (타원)
$B = 0$ and $A=C$ $\rightarrow$ circle (원)

식 (2)에 판별식을 적용해보면

\tag{3} \begin{aligned} B^2-4AC &= \left(2\sum_{i=1}^N x_{i1} x_{i2} \right)^2 - 4\left(\sum_{i=1}^N x_{i1}^2 \right)\left(\sum_{i=1}^N x_{i2}^2 \right) \\ &= 4\left[ \left(\sum_{i=1}^N x_{i1} x_{i2} \right)^2 - \left(\sum_{i=1}^N x_{i1}^2 \right)\left(\sum_{i=1}^N x_{i2}^2 \right) \right] < 0 \end{aligned}

과 같으므로 MSE contour는 항상 타원의 형태를 갖는다. 식 (3)의 마지막 부등호 관계식은 Cauchy-Schwartz inequality에 의해 언제나 성립한다.

Ridge Regression

다중회귀모델에서 살펴본 바와 같이, 규제기법이 적용되지 않은 회귀 모델은 다음과 같이 오차제곱합(Sum of Squared Error, SSE)을 최소화하여 최적의 회귀 계수를 구한다. 반면, Ridge regression은 다음과 같이 L2 제약식이 포함된 목적식을 최소화하는 회귀계수 $\bm{\beta}$ 를 찾는다.

\tag{4} \hat{\bm{\beta}} = \argmin_{\bm{\beta}}\left(\mathbf{y} - \mathbf{X}\bm{\beta}\right)^T \left(\mathbf{y} - \mathbf{X}\bm{\beta}\right) \ \ \ s.t. \ \ \|\bm{\beta}\|^2 < t

위 식의 첫 번째 항은 training accuracy를 높이기 위해 SSE를 최소화한다. 반면, 두 번째 항은 특정 독립변수에 해당하는 회귀계수가 지나치게 커져 다른 독립변수들의 설명력을 저하시키는 것을 방지한다. 즉, 오버피팅을 방지하여 모델의 일반화 성능을 높인다.

식 (4)에서 $\mathbf{X}$ 는 독립변수들로 구성된 feature matrix를 나타내며, 다중회귀모델에서도 언급했던 것처럼 각 독립변수들은 표준화되어 평균이 0이고 분산은 1이다. 참고로 $\mathbf{y}$ 도 반드시 표준화되어야 한다. 독립변수와 종속변수를 반드시 표준화하여야 하는 이유는 식 (4)에서 찾을 수 있다. 우리가 원하는 것은 제약식을 만족하면서 SSE를 최소화하는 것인데, 제약식은 회귀계수의 제곱의 합을 $t$ 로 제한한다. 따라서 독립변수마다 값의 범위가 다르게 되면, 큰 값의 범위를 갖는 독립변수들은 제약식에 의해 설명력을 잃게 될 것이다. 따라서 모든 독립변수에 동일한 가중치를 주기 위해 반드시 표준화를 해주어야 한다. $\mathbf{X}$ 형태는 다음과 같다.

\tag{5} \mathbf{X} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1k}\\ 1 & x_{21} & x_{22} & \cdots & x_{2k}\\ \vdots & \vdots & \vdots & \ddots & \vdots &\\ 1 & x_{N1} & x_{N2} & \cdots & x_{Nk}\\ \end{bmatrix}

이제 식 (4)의 해를 구하기 위해 Lagrange multiplier를 이용하여 제약식을 목적식에 올려보자.

\tag{6} \hat{\bm{\beta}} = \argmin_{\bm{\beta}}\left(\mathbf{y} - \mathbf{X}\bm{\beta}\right)^T \left(\mathbf{y} - \mathbf{X}\bm{\beta}\right) +\lambda \left(\|\bm{\beta}\|^2-t\right)

식 (6)의 해를 구하기 위해 (6)의 우변을 $J$ 라 하고 $\bm{\beta}$ 로 미분하여 그 결과가 0이 되도록하면

\tag{7} \frac{\partial J}{\partial \bm{\beta}} = -2\mathbf{X}^T \mathbf{y} + 2\left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right)\bm{\beta} = 0

이 된다. 따라서 Ridge regression의 closed-form solution은 다음과 같이 주어진다.

\tag{8} \hat{\bm{\beta}} = \left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right) ^{-1} \mathbf{X}^T \mathbf{y}

Ridge regression에서는 shrinkage parameter $\lambda$ 의 값에 따라 최적의 회귀계수 값이 달라지게 된다. $\lambda$ 가 클수록 회귀계수의 분산은 작아지는 대신 바이어스가 증가하여 모델이 더 일반화된다. 그러나 $\lambda$ 가 너무 크게 되면 모델은 언더피팅 될 수 있다.

$\hat{\bm{\beta}}$ 를 구할 때, 수치적 안정성을 높이기 위해서는 $\left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right)$ 의 역행렬을 안정적으로 구할 수 있어야 한다. 따라서 $\left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right) ^{-1}$ 의 조건수 (condition number)를 미리 정하고 $\mathbf{X}^T\mathbf{X}$ 의 eigenvalue를 추정하여 $\lambda$ 를 다음과 같이 정할 수 있다.

\tag{9} \lambda = \frac{\delta_{max} - \delta_{min}k_{target}}{k_{target}-1}

여기서 $\delta_{max}$ 와 $\delta_{min}$ 은 각각 $\mathbf{X}^T\mathbf{X}$ 의 maximum eigenvalue와 minimum eigenvalue를 나타낸다. 그리고 $k_{target}$ 은 목표하는 condition number를 의미한다. 식 (9)와 같은 방법으로 $\lambda$ 를 결정하려면 $\delta_{max}$ 와 $\delta_{min}$ 을 찾아야 한다. 익히 알려진 eigenvalue decomposition을 사용해도 되겠지만 matrix의 크기가 큰 경우 많은 자원이 소모되므로 가능하다면 $\delta_{max}$ 와 $\delta_{min}$ 만 추정하는 것이 바람직한데, power iteration 방법을 사용하면 이것이 가능하다. 식 (9)와 같은 방법으로 $\lambda$ 를 선택하면 $\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I}$ 의 condition number는 $k_{target}$ 이 된다 [6]. 참고로 Ridge regression은 Tikhonov regularization(티호노프 정칙화)의 special case이다.

$\lambda =0$ 일 때, $\hat{\bm{\beta}}$ 은 $\bm{\beta}$ 의 unbiased estimate이다. 그러나 Ridge regression은 biased estimator이다. 즉, 다음이 성립한다.

\tag{10} \begin{aligned} E \left(\hat{\bm{\beta}}\right) &= \left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right) ^{-1} \mathbf{X}^T E \left(\mathbf{y}\right) \\ &= \left(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \right) ^{-1} \mathbf{X}^T\mathbf{X}\bm{\beta} \\ &\neq \bm{\beta} \end{aligned}

Ridge regression은 regularization term $\lambda$ 를 추가함으로 인해 unbiased estimation 특성을 잃게 되었지만 대신 회귀 계수를 보다 안정적으로 추정할 수 있게 해준다. 회귀 계수를 안정적으로 추정할 수 있게 된다는 의미는 데이터가 바뀌더라도 추정된 회귀 계수의 값이 크게 변하지 않음을 의미하며, 이를 분산이 작아졌다고 표현한다. 즉, 분산과 바이어스는 서로 trade-off 관계에 있으며, 이를 bias-variance trade-off 관계라 부른다.

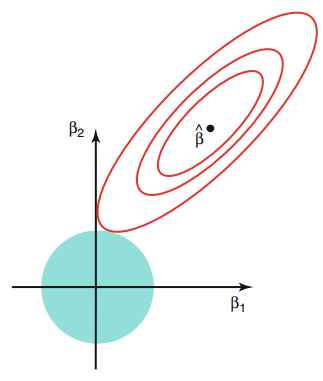
[그림 3] Ridge Regression의 solution path: L2규제와 MSE Contour의 관계

[그림 3]은 앞에서 살펴본 MSE contour를 Ridge regression에 대하여 그린 예제이다. L2 규제가 없다면 MSE(SSE)를 최소화하는 최적의 회귀계수의 좌표는 [그림 3]에서 $\hat{\bm{\beta}}$ 에 위치한다. 그러나 L2 제약식에 의해 $|\beta_1|^2 + |\beta_2|^2 < t$ 를 만족하여야 하므로 [그림 3]의 예제에서는 원의 둘레와 MSE contour가 만나는 지점에서 Ridge regression의 최적해를 찾을 수 있다.

LASSO Regression

LASSO 알고리즘은 Least Absolute Shrinkage and Selection Operator의 약어이며, 용어 그대로 회귀계수의 값을 작아지도록 Shrinkage함과 동시에 중요한 변수를 자동으로 Selection 하는 기능을 제공한다. Ridge regression에서는 L2 제약식을 가한 반면, LASSO regression은 L1 제약식을 적용한 방법이다. LASSO regression의 목적함수와 제약식은 다음과 같다.

\tag{11} \hat{\bm{\beta}} = \argmin_{\bm{\beta}}\left(\mathbf{y} - \mathbf{X}\bm{\beta}\right)^T \left(\mathbf{y} - \mathbf{X}\bm{\beta}\right) \ \ \ s.t. \ \ \|\bm{\beta}\| < t

Ridge regression은 L2 minimuzation 문제이기 때문에 미분을 통해 closed-form solution을 바로 구할 수 있지만2 L1 minimization 문제인 LASSO는 아직까지 closed-form solution을 구할 수 있는 방법이 알려져있지 않다. 때문에 다음과 같은 수치최적화 기법을 사용한다 [3]. (나중에 기회가 되면 별도의 주제로 다루기로 한다.)

Quadratic Programming
LARS Algorithm
Coordinate Descent Algorithm

LASSO의 중요한 특징은 덜 중요한 특성의 가중치를 제거하여 sparse model을 만든다는 것이다. 아래 그림 [4]는 규제 파라메터 $\lambda$ 의 크기 변화에 따른 추정된 회귀계수들의 값 변화를 나타낸다. $\lambda$ 키울수록 (식 (11)에서는 $t$ 를 키울수록) 더 많은 회귀 계수의 값들이 0이 되며, 따라서 자동으로 설명력이 높은 변수들만 선택해주는 기능을 제공한다. 다중회귀모델에서 소개한 변수선택 기법들은 통계적 기준을 바탕으로 사람이 수동으로 변수를 제거해주어야 하는 반면, LASSO는 이러한 번거로움을 완전히 해소해준다. 참고로 Ridge regression은 설명력이 낮은 변수에 해당하는 회귀계수 값을 매우 작도록 억압하기는 하지만 완전히 0으로 만들지는 못한다3.

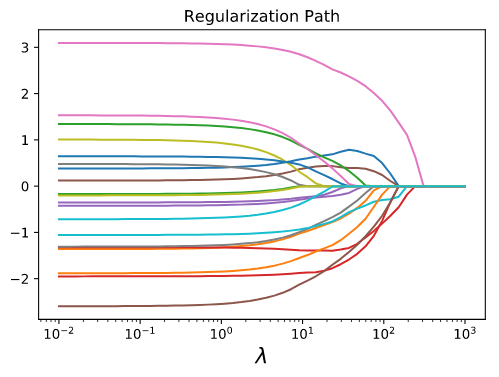
[그림 4] Regularization 값에 따른 LASSO Solution 변화 (source: [9])

앞서 Ridge regression의 solution path는 [그림 3]과 같이 표현할 수 있음을 살펴보았다. LASSO regression은 L1 규제를 사용하므로 constraint를 만족하는 공간을 [그림 5]와 같이 2차 평면상에서 마름모 형태로 나타낼 수 있다. LASSO 해는 보통 마름모의 꼭지점과 MSE contour가 만나는 지점에서 형성되는데, 이로 인해 LASSO 알고리즘을 통해 변수선택을 할 수 있게 되는 것이다. 규제 파라메터의 값이 크지 않다면 [그림 4]와 같이 모든 회귀계수 값이 0이 아니게 될 수도 있는데 이 경우는 LASSO 알고리즘의 특성을 누릴만큼 규제 파라메터 값을 작게하였기 때문에 사실상 orninary least square (OLS)와 거의 유사한 해를 갖는다고 보면 된다.

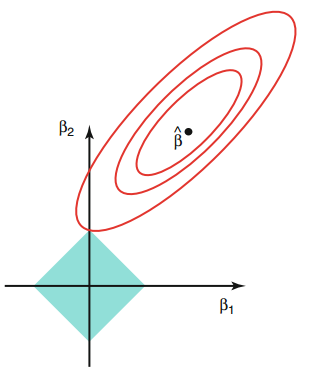
[그림 5] LASSO Regression의 solution path: L1규제와 MSE Contour의 관계

아래의 [그림 6]은 ridge regression과 LASSO regression에 경사하강법을 적용하였을 경우의 solution path를 나타낸다. Ridge regression은 L2 규제를 사용하기 때문에 항상 미분 가능하므로 최적점에 보다 매끄럽게 도달한다. 반면, LASSO는 L1 규제로 인해 특정 회귀 계수 값이 0인 지점에서는 불연속이 발생하여 미분이 불가능하다. 따라서 [그림 6]의 우측 상단에서 보이는 바와 같이 특정 회귀계수의 값이 0이 되었을 때 진동이 발생한다. (이 지점에서의 그레디언트는 $+1$ 또는 $-1$ 이다.)

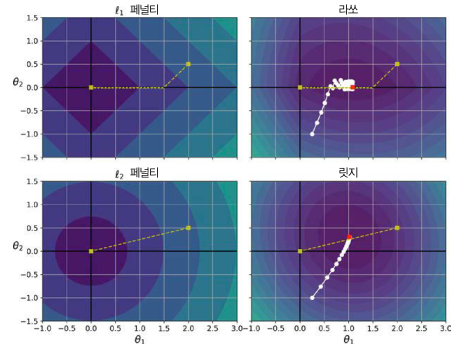
[그림 6] Ridge Regression과 LASSO Regression의 Solution Path 비교 (source: [8])

LASSO regression에 경사하강법을 적용할 때, 최적점 근처에서 MSE가 진동하는 것을 막으려면 훈련하는 동안 점진적으로 학습률을 감소시켜야 한다 [8]. 그리고 LASSO는 $\beta_i=0$ 에서 미분 가능하지 않으므로 $\beta_i=0$ 일 때는 sub-gradient vector를 사용한다. LASSO regression에서의 sub-gradient vector는 다음과 같이 나타낼 수 있다 [8].

\tag{12} g\left(\bm{\beta}\right) = \nabla_{\bm{\beta}} MSE\left(\bm{\beta}\right) + t \begin{bmatrix} sign(\beta_1) \\ sign(\beta_2) \\ \vdots \\ sign(\beta_k) \end{bmatrix}

여기서 $t$ 는 식 (11)에서 정의된 규제 파라메터를 나타내며, $sign(\beta_i)$ 는 다음과 같이 정의된다.

\tag{13} sign(\beta_i) = \begin{cases} -1, & \beta_1 < 0 \\ \ \ \ 0, & \beta_1 = 0 \\ +1, & \beta_1 > 0 \end{cases}

Elastic-Net Regression

엘라스틱넷은 Ridge와 LASSO를 합쳐 놓은 형태이며, 목적식은 다음과 같다.

\tag{14} \hat{\bm{\beta}} = \argmin_{\bm{\beta}}\left(\mathbf{y} - \mathbf{X}\bm{\beta}\right)^T \left(\mathbf{y} - \mathbf{X}\bm{\beta}\right) \ \ \ s.t. \ \ \ \alpha|\bm{\beta}\| + (1-\alpha)\|\bm{\beta}\|^2 < t

엘라스틱넷은 $\alpha$ 가 0에 가까울수록 Ridge regression과 그 특성이 유사해지며, 반대로 $\alpha$ 가 1에 가까울수록 LASSO와 유사한 특성을 갖는다. 엘라스틱넷은 표면적으로는 단순히 L1 norm과 L2 norm을 혼합한 형태에 불과해보이지만 사실 이 둘을 동시에 사용함으로써 변수 간 grouping effect를 제공하는 엄청난 이점을 갖게 된다. 즉, 변수간 상관관계가 큰 변수들에 유사한 가중치를 줌으로써 중요한 변수들은 똑같이 중요하게 취급하고 중요하지 않은 변수들은 모두 공평하게 중요하지 않게 취급한다. 즉, 변수간 상관관계가 크더라도 중요하지 않은 변수들을 모두 버리면서 중요한 변수들만 잘 골라내어 중요도와 상관관계에 따라 적합한 가중치를 적용할 수 있다.

엘라스틱넷의 penalty 함수는 [그림 3]과 [그림 5]의 중간 형태를 갖는다. 이 부분은 설명이 중복되므로 여기서는 생략한다. (구글에 검색하면 그림 많이 나옴.)

Summary

여기까지 살펴본 ridge regression과 LASSO regression의 차이를 간단히 정리하자면 다음과 같다.

Ridge는 L2 norm, LASSO는 L1 norm을 사용
Ridge는 불필요한 변수에 대한 가중치를 0에 가깝게 줄이는 반면, LASSO는 불필요한 변수에 대한 가중치를 완전히 0으로 억압하여 변수선택 기능 제공
Ridge는 미분 가능하므로 보다 매끄럽게(?) 최적점에 도달하는 반면, LASSO는 0에서 미분 가능하지 않음므로 진동하며 수렴
Ridge는 closed-form solution 제공, 미분 가능하므로 경사하강법 적용 가능
LASSO는 numerical optimization 문제를 풀어야 하며, sub-gradient vector를 사용하여 경사하강법 적용
(본문에서 살펴보지 않은 내용) Ridge는 변수 간 상관관계가 높은 경우(즉, colinearity가 큰 경우) 좋은 예측 성능을 보이는 것으로 알려져 있으나, LASSO는 이 경우 변수 선택 성능이 저하되어 좋지 못하 성능을 제공한다. [3].

그렇다면 Ridge, LASSO, Elastic-Net을 언제 사용해야 할까? 대부분의 머신러닝 문제(나아가 많은 estimation 문제)에서 약간의 regularization이 있는 것이 그렇지 않은 경우보다 더 좋은 성능을 제공한다. 따라서 일반적인 선형회귀는 피하는 것이 좋으며, 기본적으로는 Ridge regression을 많이 사용한다. Ridge regression이 제 1 옵션이지만 중요한 변수의 개수가 몇 개뿐이고 변수 간 상관관계가 적다고 판단되면 LASSO를 사용하는게 낫다. 중요한 특성의 수가 적지만 특성 간 상관관계가 있다고 판단되면 Elastic-Net이 더 선호된다.

Keras Example [8]

# Ridge Regression
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])

# Ridge Regression using SGD
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])

# LASSO Regression
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])

# Ridge Regression using SGD
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(penalty="l1")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])

# Elastic-Net
from sklearn.linear_model import ElasticNet
elastic_reg = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_reg.fit(X, y)
elastic_reg_.predict([[1.5]])

Footnotes

1: 이전 포스트에서 살펴본 바와 같이 다항회귀모델은 다중회귀모델로 표현할 수 있다.

2: 물론 Ridge Regression도 차원이 큰 경우 경사하강법을 사용하는 것이 더 유리하다. 경사하강법을 이용한 회귀모델의 구현은 이 포스트를 참고하면 된다.

3: 편법(?)이기는 하지만 Ridge regression 후 회귀 계수의 값이 작은 변수들을 무시하는 것도 변수 선택을 하는데 있어 손쉬운 방법 중 하나이다. 이렇게 선택된 변수로 Ridge Regression을 한 번 더 수행하면 대부분의 경우 잘 동작한다.

References

[1] 조우쯔화 저/김태헌 역, "단단한 머신러닝 머신러닝 기본 개념을 제대로 정리한 인공지능 교과서," 제이펍, 2020.

[2] 장철원, "선형대수와 통계학으로 배우는 머신러닝 with 파이썬 최적화 개념부터 텐서플로를 활용한 딥러닝까지," 비제이퍼블릭, 2021.

[3]김성범, [핵심 머신러닝] 정규화 모델 1(Regulariztion 개념, Ridge Regression)](https://www.youtube.com/watch?v=pJCcGK5omhE&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=21)

[4] https://en.wikipedia.org/wiki/Conic_section

[5] http://www.adeveloperdiary.com/data-science/how-to-visualize-gradient-descent-using-contour-plot-in-python/

[6] Tabeart, Jemima M., et al. "Improving the condition number of estimated covariance matrices." Tellus A: Dynamic Meteorology and Oceanography 72.1 (2020): 1-19.

[7] https://towardsdatascience.com/from-linear-regression-to-ridge-regression-the-lasso-and-the-elastic-net-4eaecaf5f7e6

[8] 오렐리앙 제롱 (박해선 역), "핸즈온 머신러닝 사이킷런과 텐서플로를 활용한 머신러닝, 딥러닝 실무 2판," 한빛미디어, 2020.

[9] http://www.incodom.kr/Lasso_regression