Activation Functions

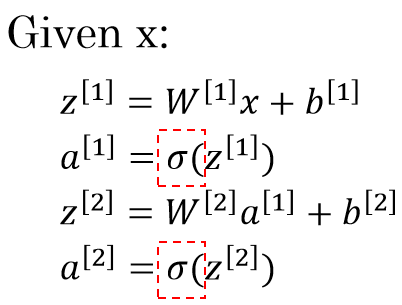logistic regression에서 linear transformation 결과에 적용한 non-linear transformation인 sigmoid함수가 activation function에 해당된다.
activation function은 미분만 가능하다면, 즉 gradient 계산만 가능하다면 어떤 non-linear function도 사용가능하다. 근래에 sigmoid 함수는 주로 output layer에만 사용되고 hidden layer에서는 사용되지 않는 추세이다.

Sigmoid

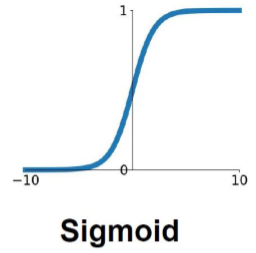
sigmoid는 [0,1]범위에 a를 분포시킨다.

하지만 exponent가 있기 때문에 계산하는데에 시간이 오래걸리고 z의 값이 커지면 gradient가 매우 작아지는 vanishing gradient 문제가 있으며 sigmoid의 결과는 zero-centered가 아닌 단점이 있다.

sigmoid를 통과한 output은 zero-output이 아니라 전부 positive이기 때문에 생기는 문제점은 다음과 같다.
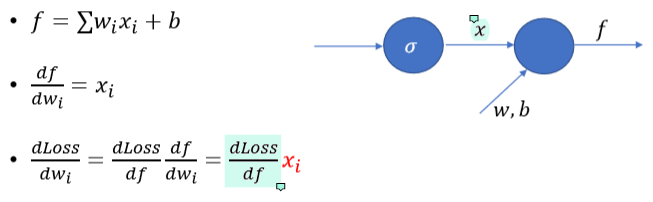
sigmoid를 통과하여 나온 x가 전부 양수가 되면서 모든 dLoss/dw의 부호가 dLoss/df의 부호에 따라 정해지게 된다.
f가 scalar이기 때문에 dLoss/df도 항상 하나의 scalar값으로 결정되면서 모든 dLoss/dw가 양수 혹은 음수의 하나의 부호만 갖게 된다. w가 1000개든 100000개든 전부 같은 부호를 갖는 것이다. 이렇게 값들이 극단적으로 나오면서 아래와 같이 지그재그형식으로 learning을 하게 된다.
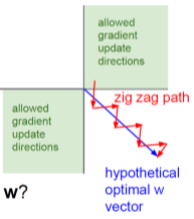이 점이 굉장히 비효율적이기 때문에 sigmoid는 output layer가 아닌 hidden layer에서는 거의 쓰이지 않는다.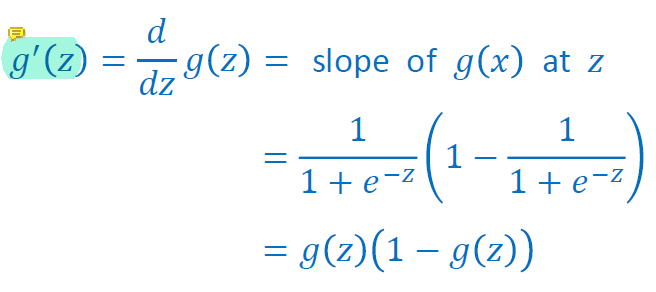

tanh (Hyperboic Tangent)

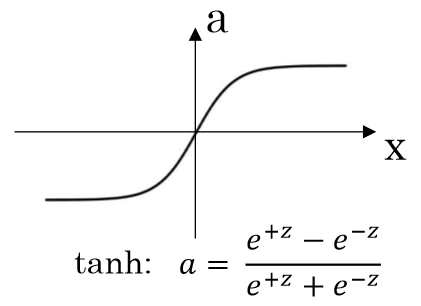
tanh는 수학적으로 sigmoid가 shift된 function이다. tanh는 output이 [-1,1]안으로 나오기 때문에 zero-centered이고, zig-zag dynamic이 없다. 그렇기에 tanh는 보통 sigmoid보다 항상 더 좋은 결과를 낸다고 알려져있다(make learning easier).

하지만 exponent가 4개이기 때문에 시간이 오래걸리는, expensive한 방법이다.

또한 그래프 양 끝의 기울기가 0에 수렴하기 때문에 입력이 엄청나게 크거나 작으면 gradient의 값이 너무 작아 gradient를 거의 update하지 못하기 때문에 gradient descent의 의미가 없다. 이것을 vanishing gradient라고 한다.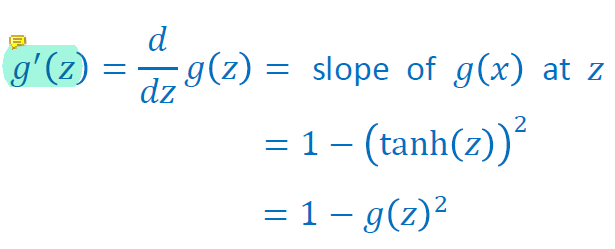

ReLU (Rectified Linear Unit)

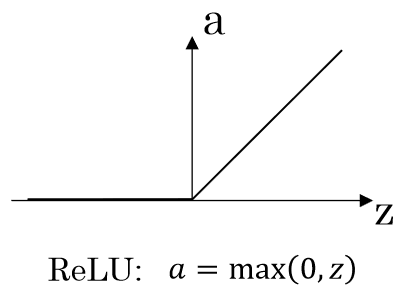
ReLU는 most common activation function이다. 음수 값은 전부 0으로 만들고 음수가 아니라면 자기 자신의 값이 그대로 나온다. 하지만 ReLU도 z가 음수일 때 vanishing gradient문제가 있다.

ReLU를 activation function으로 사용하는 이유는 쓸모있는 신호만 남겨두고 나머지 신호는 제외하기 위해서이다. ReLU를 통과하면 상대적으로 중요한 정보만 남게 된다. 즉, ReLU를 이용하면 좋은 신호는 양수로 보내고 안좋은 신호는 음수로 보내는 W와 b를 learning하게 된다.

ReLU를 사용할 때 z=0인 부분에서는 미분을 할 수 없지만 그 때에는 미분값이 0이라고 가정하고 사용한다.

ReLU는 zero-centered가 아니기 때문에 지그재그 문제를 어느정도 가지고 있지만 계산이 엄청나게 빠르고 확실하게 필요없는 정보를 차단할 수 있기 때문에 자주 사용된다.
함수마다 장단점이 있고 막상 써보기 전까지는 좋을지 안좋을지 알 수 없지만 ReLU는 많은 경우에 좋다고 알려져 있다.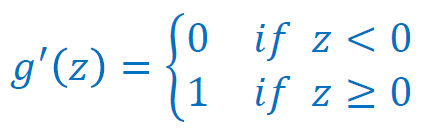

Leaky ReLU

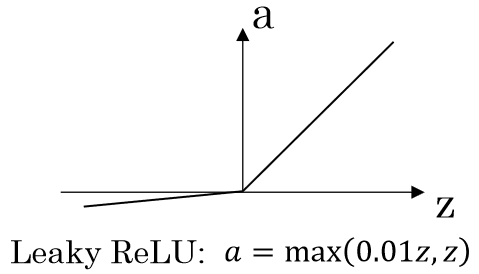
ReLU의 vanishing gradient문제를 해결하기 위해 고안된 activation function이다. Leaky ReLU의 경우에는 모든 경우에 gradient가 있기 때문에 vanishing gradient문제가 없다.

굉장히 빠르고 우수하다고 알려져있지만 사람들은 관례를 따라 ReLU를 사용하는 경향이 있다. 그런 경우들은 대부분 ReLU를 Leaky ReLU로 대체하였을 때 더 좋은 성능을 낸다.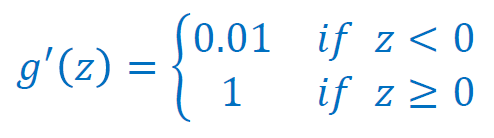

PReLU (Parametric Rectifier Linear Unit)

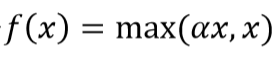
PReLU는 α가 0.01이 되면 Leaky ReLU와 동일해진다.

PReLU는 α를 하나의 training해야하는 변수로 놓고 α도 training을 한다. 따라서 expensive하지만 결과가 좋은 축에 속한다.
Leaky ReLU의 general한 버전으로, α를 unknown variable로 두고 이 값도 같이 찾아서 dLoss/dα를 구할 수 있다.

ELU (Exponential Linear Units)

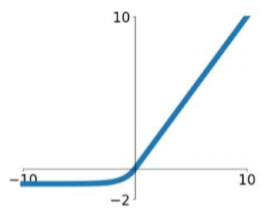
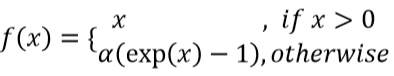
ELU는 ReLU의 모든 장점을 가지고 있다.
Leaky ReLU의 경우 vanishing gradient문제를 피하기 위해서 모든 값이 gradient를 갖기 때문에 완벽하게 이상한 값이 들어왔을 때 완벽하게 쳐내지 못한다는 단점이 있다. Leaky ReLU의 경우 -1000이 들어오면 -10은 없애지 못하고 남게 된다. 그런 점이 싫어서 엄청나게 이상한 값이 들어왔을 때 쳐낼 수 있도록 고안된 함수이다.

vanishing gradient문제가 있고 좋다고 알려져 있지만 잘 사용되지는 않는다. exponent로 인해 expensive한 편이다.

Activation Function을 Non-Linear Function으로 사용해야하는 이유

activation function으로 linear function을 사용했다고 가정해보자.
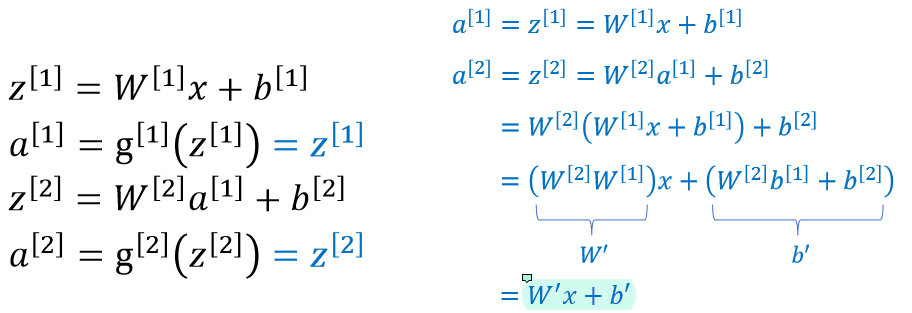linear function으로 activation function을 사용하면 final output이 단순한 linear 형태가 된다.
그렇기 때문에 결론적으로 neural network가 10층이든 100층이든 input에 대해 딱 한 번 linear transformation한 것과 같은 결과가 나오기 때문에 deep neural network를 사용하는 의미가 없어진다.