Gaussian Mixture Model
[https://untitledtblog.tistory.com/133]
- Gaussian 분포가 여러 개 혼합된 clustering algorithm
- 정규분포를 가정하고, data로부터 여러 정규분포를 혼합한 확률 모형을 찾는 과정
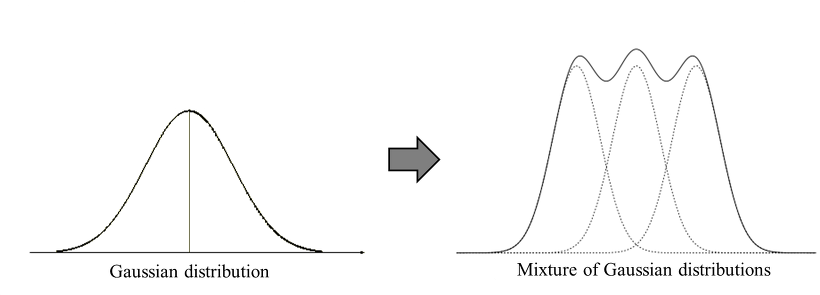
[그림 1]과 같이 K개의 Gaussian distribution을 혼합하여 표현하자는 것이 GMM의 기본 아이디어이다. (K는 hyperparameter)
각 Gaussian 분포에서 3개의 parameter를 가정
번쨰 Gaussian 분포에 대하여,
- : mixing coefficient
라면, 주어진 데이터 x에 대한 GMM은 아래와 같이 Gaussian probability density function의 함으로 표현한다.

여기서 는 k번째 gaussian distribution이 선택될 확률을 나타냄
그리고 아래 조건을 만족함
결국, GMM을 학습시킨다는 것은
데이터 로부터 적절한 , , 를 추정하는 것과 같다.
EM algorithms
곡선의 분포에 맞게 라벨링
흠..
- 분포가 주어지지 않은 상황
- 만약에 데이터가 주어졌고 정규분포의 파라미터를 가정해서 이 데이터를 가장 잘 설명하는 곡선을 찾을 수 있다.
- 데이터 라벨이 주어지지 않은 상황
곡선이 주어지면 데이터에 맞게 파라미터를 최적화하면서 데이터에 맞는 곡선을 최종적으로 찾을 수 있다.
1,2 데이터에 fitting되는 곡선을 어떻게 찾을 수 있을까?
