Lecture 13. Debugging ML Models and Error Analysis

Lecture video link: https://youtu.be/ORrStCArmP4

Advice on applying ML

• Don’t waste your time collecting data unless you have confidence that it’s useful to actually spend all that time. → Very easy to agree with, but you might end up doing things above.. Be careful.
  

Key ideas

1. Diagnostic for debugging learning algorithms

2. Error analyses and ablative analysis

3. How to get started on machine learning problem

   Premature (statistical) optimization

Andrew Ng: Even to this day, I still remember that feeling of surprise of implementing softmax algorithm.. no, there’s got to be a bug 🤣 and I went in to try to find the bug, and there wasn’t bug.

Machine learning workflow?

Implement a model

→ Check that the model does not work well

→ Decide what to do next: your ability will huge impact on efficiency.

Debugging learning algorithms

Motivating example:

• Anti-spam. You carefully choose a small set of 100 words to use as features. (Instead of using all 50000+ words in English.)
• Logistic regression with regularization (Bayesian Logistic regression), implemented with gradient descent, gets 20% test error, which is unacceptably high.

• What to do next?

Fixing the learning algorithm

• Logistic regression (with regularization):

• Common approach: Try improving the algorithm in different ways.
  • Try getting more training examples.
  • Try a smaller set of features.
  • Try a larger set of features.
  • Try changing the features: Email header vs. email body features.
  • Run gradient descent for more iterations.
  • Try Newton’s method.
  • Use a different value for $\lambda$.
  • Try using an SVM.

Andrew Ng comment: Unless you analyze these different options, it’s hard to know which of these is actually the best option. The most common diagnostic I end up using in developing learning algorithms is bias versus variance diagnostic. If a classifier has high bias, it tends to underfit the data, and if a classifier has high variance, it tends to be relatively complex.

Diagnostic for bias vs. variance

Better approach:

• Run diagnostics to figure out what the problem is.
• Fix whatever the problem is.

Logistic regression’s test error is 20% (unacceptably high).

Suppose you suspect the problem is either:

• Overfitting (high variance).
• Too few features to classify spam (high bias).

Diagnostic:

• Variance: Training error will be much lower than test error.
• Bias: Training error will also be high.

High variance → much lower error on the training set than on the development set.

High bias → training/test/dev set errors will go behind. (prediction impossible).

More on bias vs. variance

Typical learning curve for high variance:

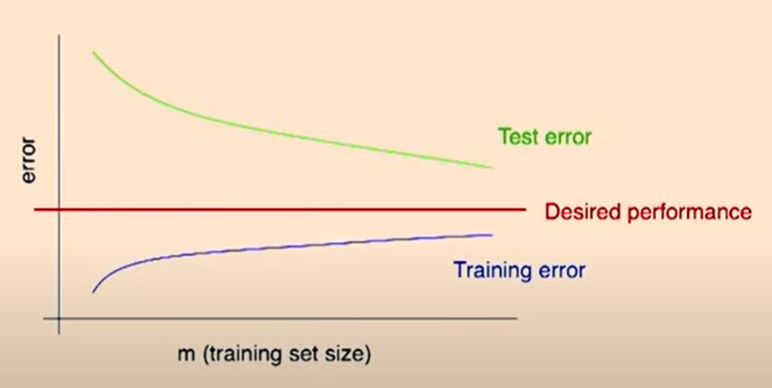
(Source: https://youtu.be/ORrStCArmP4?t=14m)

• Test error still decreasing as $m$ increases. Suggests larger training set will help.
• Large gap between training and test error.

Andrew Ng comment: If you see a learning curve looking like this, you have a variance problem.

Andrew Ng comment: If the curves look like this assuming that your training data is IID (training/dev/test sets are all drawn from the same distribution), there is a learning theory that suggests that in most cases the green curve should decay as $\frac{1}{\sqrt m}$ until it reaches some Bayes error.

Learning algorithms don’t always decay to zero in practical due to lower quality data.

Typical learning curve for high bias:

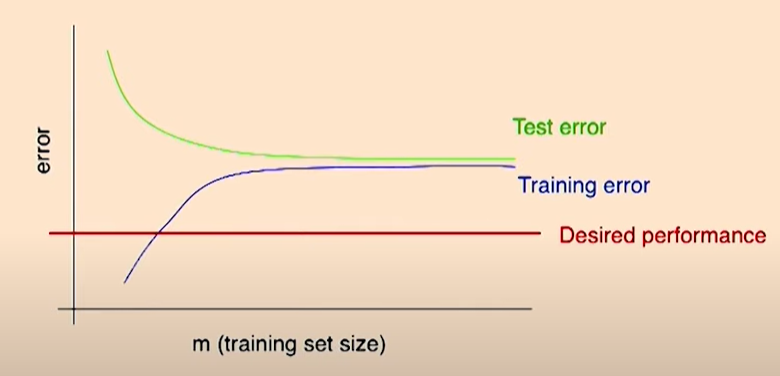
(Source: https://youtu.be/ORrStCArmP4?t=17m30s)

• Even training error is unacceptably high.
• Small gap between training and test error.

Diagnostics tell you what to try next

Logistic regression, implemented with gradient descent.

Fixes to try:

Try	Fix
Try getting more training examples.	Fixes high variance.
Try a smaller set of features.	Fixes high variance.
Try a larger set of features.	Fixes high bias.
Try email header first.	Fixes high bias.
Run gradient descent for more iterations.	Fixes optimization problem.
Try Newton’s method.	Fixes optimization problem.
Use a different value for $\lambda$.	Fixes optimization objective.
Try using an SVM.	Fixes optimization objective.

Andrew Ng comment: For a new application problem, it’s difficult to know in advance if you’re gonna run into a high bias or high variance problem (what’s gonna go wrong with your learning algorithm).

→ Advice: Implement a quick and dirty learning algorithm. And start with logistic regression. Then run this bias-variance type of analysis to see what went wrong and use it to decide what to do next (more complex algorithm? more data? etc.).

Exception: If you’re working on a domain in which you have a lot of experience.

Optimization algorithm diagnostics

• Bias vs. variance is one common diagnostic.
• For other problems, it’s usually up to your own ingenuity to construct your own diagnostics to figure out what’s wrong.
• Another example:
  • Logistic regression gets 2% error on spam, and 2% error on non-spam. (False Negative) (Unacceptably high error on non-spam)
    
  • SVM using a linear kernel gets 10% error on spam, and 0.01% error on non-spam. (False Positive) (Acceptable performance.)
    
  • But you want to use logistic regression, because of computational efficiency, etc.
• What to do next?

More diagnostics

• Other common questions:

  Is the algorithm (gradient ascent for logistic regression) converging?

  

  (Source: https://youtu.be/ORrStCArmP4?t=29m13s)

  It’s often very hard to tell if an algorithm has converged yet by looking at the objective.
  

• Are you optimizing the right function?

  I.e., what you care about:

  $a(\theta)=\sum_iw^{(i)}1\left\{h_\theta(x^{(i)})=y^{(i)}\right\}$

  (weights $w^{(i)}$ higher for non-spam than for spam).
  

• Logistic regression? Correct value for $\lambda$?

  $\max_\theta J(\theta)=\sum_{i=1}^m\log p(y^{(i)}|x^{(i)},\theta)-\lambda||\theta||^2.$

• SVM? Correct value for $C$?

  $\begin{aligned}\min_{w,b}&\;\;\;||w||^2+C\sum_{i=1}^m\xi_i\\\text{s.t.}&\;\;\;y^{(i)}(w^Tx^{(i)}-b)\ge1-\xi_i.\end{aligned}$

Second diagnostic Andrew Ng end up using: Is the problem your optimization algorithm? In other words, is gradient ascent not converging? Or is the problem that you’re just optimizing the wrong function?

Diagnostic

An SVM outperforms logistic regression, but you really want to deploy logistic regression for your application.

Let $\theta_{\text{SVM}}$ be the parameters learned by an SVM.

Let $\theta_\text{BLR}$ be the parameters learned by logistic regression. (BLR = Bayesian logistic regression.)

You care about weighted accuracy:

$\theta_\text{SVM}$ outperforms $\theta_\text{BLR}$. So:

BLR tries to maximize:

Q. Why not maximize $a(\theta)$ directly?

A. Because $a(\theta)$ is not differentiable due to indicator function. (NP-hard)

Diagnostic:

Two cases

Case 1:

But BLR was trying to maximize $J(\theta)$. This means that $\theta_\text{BLR}$ fails to maximize $J$, and the problem is with the convergence of the algorithm. Problem is with optimization algorithm.

Case 2:

This means that BLR succeeded at maximizing $J(\theta)$. But the SVM, which does worse on $J(\theta)$, actually does better on weighted accuracy $a(\theta)$.

This means that $J(\theta)$ is the wrong function to be maximizing, if you care about $a(\theta)$. Problem is with objective function of the maximization problem.

Machine learning algorithm

1. Build a simulator of helicopter.

2. Choose a cost function. Say $J(\theta)=||x-x_\text{desired}||^2$ ($x$: helicopter position).

3. Run reinforcement learning (RL) algorithm to fly helicopter in simulation, so as to try to minimize cost function:

   $\theta_\text{RL}=\argmin_\theta J(\theta).$

Suppose you do this, and the resulting controller parameters $\theta_\text{RL}$ gives much worse performance than you human pilot. What to do next?

• Improve simulator?
• Modify cost function $J$?
• Modify RL algorithm?

How helicopter works: https://science.howstuffworks.com/transport/flight/modern/helicopter6.htm

Debugging an RL algorithm

The controller given by $\theta_\text{RL}$ performs poorly.

Suppose that:

1. The helicopter simulator is accurate.
2. The RL algorithm correctly controls the helicopter (in simulation) so as to minimize $J(\theta)$.
3. Minimizing $J(\theta)$ corresponds to correct autonomous flight.

Then: The learned parameters $\theta_\text{RL}$ should fly well on the actual helicopter.

Diagnostics:

1. If $\theta_\text{RL}$ flies well in simulation, but not in real world, then the problem is in the simulator. Otherwise:

Q. Is there ever the case that it flies bad in the simulator but well in real world?

A. I (Andrew Ng) wish that happened. 🤣

Andrew Ng comment: If we throw a lot of noise in the simulation environment, it is likely that the real world trial tends to be robust.

1. Let $\theta_\text{human}$ be the human control policy. If $J(\theta_\text{human})<J(\theta_\text{RL})$, then the problem is in the reinforcement learning algorithm. (Failing to minimize the cost function $J$.)
2. If $J(\theta_\text{human})\ge J(\theta_\text{RL})$, then the problem is in the cost function. (Maximizing it doesn’t correspond to good autonomous flight.)

Andrew Ng comment: Finding a good cost function is actually really difficult.

Error analysis

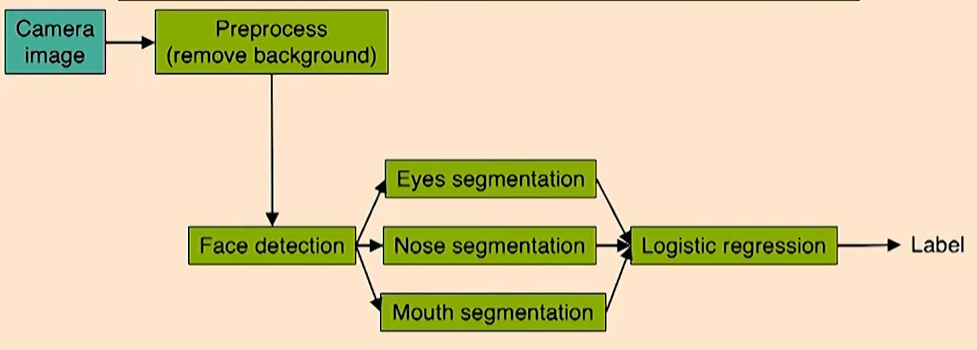
Many applications combine many different learning components into a ‘pipeline.’ E.g., face recognition images: [artificial example].

(Source: https://youtu.be/ORrStCArmP4?t=1h04m)

Andrew Ng comment: A lot of machine learning applications are usually not just one learning algorithm. Instead, you have a pipeline to string together many different steps.

Q. How do you actually build a face recognition algorithm to decide if someone approaching your front door is authorized to unlock the door?

→ Start with a camera image

→ Preprocess to remove the background.

Andrew Ng comment: Having a lot of data is great. I love having more data. But big data has also been a little bit over-hyped. To model things, you could do with small data sets as well. And in the teams I’ve worked with we find that if you have a relatively small dataset, often you can still get great results.

But when you have a relatively small data, you need to construct more insightful design of machine learning pipelines.

How much error is attributable to each of the components?

Plug in ground-truth for each component, and see how accuracy changes.

Component	Accuracy
Overall system	85%
Preprocess (remove background)	85.1%
Face detection	91%
Eyes segmentation	95%
Nose segmentation	96%
Mouth segmentation	97%
Logistic regression	100%

Q. If you do face detection accurately and your error drops, what does it entail?

A. It’s not impossible for that to happen, it would be quite rare. I (Andrew Ng) would scrutinize what’s going on actually.

Whenever you find one of these weird things, I wouldn’t gloss over and ignore it. I would go in and figure out what’s going on.

Ablative analysis

Simple logistic regression without any clever features get 94% performance.

Just what accounts for your improvement from 94 to 99.9%?

Ablative analysis: Remove components from your system one at a time, to see hot it breaks.

Component	Accuracy
Overall system	99.9%
Spelling correction	99.0%
Sender host features	98.9%
Email header features	98.9%
Email text parser features	95%
Javascript parser	94.5%
Features from images	94.0% [baseline]

Conclusion: The email text parser features account for most of the improvement. $\leftarrow$ insight !