Outline
EM convergence
Gaussian propotion
Factor analysis
Gaussian marginals vs. conditionals
EM steps
Recap
E-step:
Q i ( z ( i ) ) : = p ( z ( i ) ∣ x ( i ) ; θ ) . Q_i(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta). Q i ( z ( i ) ) : = p ( z ( i ) ∣ x ( i ) ; θ ) . M-step:
θ : = arg max θ ∑ i ∑ z ( i ) Q i ( z ( i ) ) log p ( x ( i ) , z ( i ) ; θ ) Q i ( z ( i ) ) . \theta:=\argmax_\theta\sum_i\sum_{z ^{(i)}}Q_i(z ^{(i)})\log\frac{p(x ^{(i)},z ^{(i)};\theta)}{Q_i(z ^{(i)})}. θ : = θ a r g m a x i ∑ z ( i ) ∑ Q i ( z ( i ) ) log Q i ( z ( i ) ) p ( x ( i ) , z ( i ) ; θ ) . p ( x ( i ) , z ( i ) ) = p ( x ( i ) ∣ z ( i ) ) p ( z ( i ) ) p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)}) p ( x ( i ) , z ( i ) ) = p ( x ( i ) ∣ z ( i ) ) p ( z ( i ) )
z ( i ) ∼ Multinomial ( ϕ ) z^{(i)}\sim\text{Multinomial}(\phi) z ( i ) ∼ Multinomial ( ϕ )
[ p ( z ( i ) = j ) = ϕ j ] [p(z^{(i)}=j)=\phi_j] [ p ( z ( i ) = j ) = ϕ j ]
x ( i ) ∣ z ( i ) = j ∼ N ( μ j , Σ j ) x^{(i)}|z^{(i)}=j\sim\mathcal N(\mu_j,\Sigma_j) x ( i ) ∣ z ( i ) = j ∼ N ( μ j , Σ j )
E-step:
w j ( i ) = Q i ( z ( i ) = j ) = p ( z ( i ) = j ∣ x ( i ) ; ϕ , μ , Σ ) . w_j^{(i)}=Q_i(z^{(i)}=j)=p(z^{(i)=j}|x^{(i)};\phi,\mu,\Sigma). w j ( i ) = Q i ( z ( i ) = j ) = p ( z ( i ) = j ∣ x ( i ) ; ϕ , μ , Σ ) . M-step:
max ϕ , μ , Σ ∑ i ∑ z ( i ) Q i ( z ( i ) ) log p ( x ( i ) , z ( i ) ; ϕ , μ , Σ ) Q i ( z ( i ) ) = max ∑ i ∑ j w j ( i ) log 1 ( 2 π ) n / 2 ∣ Σ j ∣ 1 / 2 exp ( − 1 2 ( x ( i ) − μ j ) Σ j − 1 ( x ( i ) − μ j ) T ) ϕ j w j ( i ) = : max f \begin{aligned}&\max_{\phi,\mu,\Sigma}\;\sum_i\sum_{z^{(i)}}Q_i(z ^{(i)})\log\frac{p(x ^{(i)},z ^{(i)};\phi,\mu,\Sigma)}{Q_i(z ^{(i)})}\\&=\max\sum_i\sum_jw ^{(i)}_j\log\frac{\frac{1}{(2\pi)^{n/2}|\Sigma_j|^{1/2}} \exp\left(-\frac{1}{2}(x ^{(i)}-\mu_j)\Sigma_j^{-1} (x ^{(i)}-\mu_j)^T\right)\phi_j}{w_j^{(i)}}\\&=:\max f\end{aligned} ϕ , μ , Σ max i ∑ z ( i ) ∑ Q i ( z ( i ) ) log Q i ( z ( i ) ) p ( x ( i ) , z ( i ) ; ϕ , μ , Σ ) = max i ∑ j ∑ w j ( i ) log w j ( i ) ( 2 π ) n / 2 ∣ Σ j ∣ 1 / 2 1 exp ( − 2 1 ( x ( i ) − μ j ) Σ j − 1 ( x ( i ) − μ j ) T ) ϕ j = : max f ∇ μ j f = set 0 ⟹ μ j = ∑ i w j ( i ) x ( i ) ∑ i w j ( i ) . \begin{aligned}&\nabla_{\mu_j}f\stackrel{\text{set}}{=}0\\&\Longrightarrow\mu_j=\frac{\sum\limits_iw_j ^{(i)}x ^{(i)}}{\sum\limits_iw_j^{(i)}}.\end{aligned} ∇ μ j f = set 0 ⟹ μ j = i ∑ w j ( i ) i ∑ w j ( i ) x ( i ) . w j ( i ) w_j^{(i)} w j ( i ) x ( i ) x ^{(i)} x ( i ) j j j
p ( z ( i ) = j ∣ x ( i ) ; ⋯ ) p(z ^{(i)}=j|x ^{(i)};\cdots) p ( z ( i ) = j ∣ x ( i ) ; ⋯ ) ∇ ϕ j f = set 0 ⟹ ϕ j = ∑ i w j ( i ) ∑ i ∑ j w j ( i ) = 1 n ∑ i w j ( i ) . \begin{aligned}&\nabla_{\phi_j}f\stackrel{\text{set}}{=}0\\&\Longrightarrow\phi_j=\frac{\sum\limits_iw_j ^{(i)}}{\sum\limits_i\sum\limits_jw_j^{(i)}}= \frac{1}{n} \sum\limits_iw_j ^{(i)}.\end{aligned} ∇ ϕ j f = set 0 ⟹ ϕ j = i ∑ j ∑ w j ( i ) i ∑ w j ( i ) = n 1 i ∑ w j ( i ) . Define
J ( θ , Q ) = ∑ i ∑ z ( i ) Q i ( z ( i ) ) log p ( x ( i ) , z ( i ) ; θ ) Q i ( z ( i ) ) . J(\theta,Q)=\sum_i\sum_{z ^{(i)}}Q_i(z ^{(i)})\log\frac{p(x ^{(i)},z ^{(i)};\theta)}{Q_i(z ^{(i)})}. J ( θ , Q ) = i ∑ z ( i ) ∑ Q i ( z ( i ) ) log Q i ( z ( i ) ) p ( x ( i ) , z ( i ) ; θ ) . We know
l ( θ ) ≥ J ( θ , Q ) l(\theta)\ge J(\theta,Q) l ( θ ) ≥ J ( θ , Q ) for any θ , Q \theta, Q θ , Q
E-step:
Maximize J J J Q Q Q
M-step:
Maximize J J J θ \theta θ
Mixture of Gaussian
Say n = 2 , m = 100 n=2,m=100 n = 2 , m = 1 0 0 m ≫ n m\gg n m ≫ n
n ≈ m n\approx m n ≈ m n ≫ m n\gg m n ≫ m
Model as single Gaussian:
X ∼ N ( μ , Σ ) X\sim\mathcal N(\mu,\Sigma) X ∼ N ( μ , Σ ) MLE:
μ = 1 m ∑ i x ( i ) Σ = 1 m ∑ i ( x ( i ) − μ ) ( x ( i ) − μ ) T \begin{aligned}\mu&=\frac{1}{m}\sum_ix^{(i)}\\\Sigma&=\frac{1}{m}\sum_i(x^{(i)}-\mu)(x^{(i)}-\mu)^T\end{aligned} μ Σ = m 1 i ∑ x ( i ) = m 1 i ∑ ( x ( i ) − μ ) ( x ( i ) − μ ) T If m ≤ n m\le n m ≤ n Σ \Sigma Σ
Option 1. Constrain Σ ∈ R n × n \Sigma\in\mathbb R^{n\times n} Σ ∈ R n × n
Σ = [ σ 1 2 σ 2 2 ⋱ σ n 2 ] \Sigma=\begin{bmatrix}\sigma_1^2&&&\\&\sigma_2^2&&\\&&\ddots&\\&&&\sigma_n^2\end{bmatrix} Σ = ⎣ ⎢ ⎢ ⎢ ⎡ σ 1 2 σ 2 2 ⋱ σ n 2 ⎦ ⎥ ⎥ ⎥ ⎤ MLE:
σ j 2 = 1 m ∑ i ( x j ( i ) − μ j ) 2 . \sigma_j^2=\frac{1}{m}\sum_i(x_j^{(i)}-\mu_j)^2. σ j 2 = m 1 i ∑ ( x j ( i ) − μ j ) 2 . Q. Problem with this assumption?
A. The modeling assumes that all of your features are uncorrelated. I.e., if you have temperature sensors in a room, it’s not a good assumption to assume the temperatures at all points of the room are completely uncorrelated.
Option 2. (Stronger assumption)
Constrain Σ \Sigma Σ Σ = σ 2 I \Sigma=\sigma^2I Σ = σ 2 I
Σ = [ σ 2 σ 2 ⋱ σ 2 ] \Sigma=\begin{bmatrix}\sigma^2&&&\\&\sigma^2&&\\&&\ddots&\\&&&\sigma^2\end{bmatrix} Σ = ⎣ ⎢ ⎢ ⎢ ⎡ σ 2 σ 2 ⋱ σ 2 ⎦ ⎥ ⎥ ⎥ ⎤ MLE:
σ 2 = 1 m n ∑ i ∑ j ( x j ( i ) − μ j ) 2 . \sigma^2=\frac{1}{mn}\sum_i\sum_j(x_j^{(i)}-\mu_j)^2. σ 2 = m n 1 i ∑ j ∑ ( x j ( i ) − μ j ) 2 . What the factor analysis do?
→ It captures some of the correlations but that doesn’t run into a uninvertible covariance matrices that the naive Gaussian model does, even with 100 dimensional data and 30 examples.
Q. ?
A. Common thing to do is apply Wishart prior … add a small diagonal value to the MLE: Σ + ϵ I \Sigma+\epsilon I Σ + ϵ I
This technically takes away non-invertible matrix problem. But it’s not the best model for a lot of datasets.
Q. Why use option 2 which is even worse than option 1?
A. To develop a description for factor analysis.
Andrew Ng comment:
These days large tech companies work on similar problems.
One of the really overlooked parts of the machine learning world is small data problems. A lot of practical applications of machine learning including class projects. Small data problems feel like blind spots, or a gap of a lot of the work done in the AI world today.
Q. Why don’t we use the same algorithms with big data?
A. Andrew Ng thinks in the machine learning world we are not very good at understanding the scaling. We don’t actually have a good understanding of how to modify our algorithms.
(Facebook recently (2020) published a paper which handles 3.5 billion images and the result was cool.)
Framework:
p ( x , z ) = p ( x ∣ z ) p ( z ) p(x,z)=p(x|z)p(z) p ( x , z ) = p ( x ∣ z ) p ( z )
z ∼ hidden z\sim\text{hidden} z ∼ hidden
I.e. for d = 3 , m = 100 , n = 30 d=3,m=100,n=30 d = 3 , m = 1 0 0 , n = 3 0
z ∼ N ( 0 , I ) , z ∈ R d ( d < n ) z\sim\mathcal N(0,I), z\in\mathbb R^d\;(d<n) z ∼ N ( 0 , I ) , z ∈ R d ( d < n )
x = μ + Λ z + ϵ x=\mu+\Lambda z+\epsilon x = μ + Λ z + ϵ
where ϵ ∼ N ( 0 , Ψ ) \epsilon\sim\mathcal N(0,\Psi) ϵ ∼ N ( 0 , Ψ )
Parameters:
μ ∈ R n , Λ ∈ R n × d , Ψ ∈ R n × n , diagonal \mu\in\mathbb R^n,\Lambda\in\mathbb R^{n\times d},\Psi\in\mathbb R^{n\times n},\text{diagonal} μ ∈ R n , Λ ∈ R n × d , Ψ ∈ R n × n , diagonal
Equivalently,
x ∣ z ∼ N ( μ + Λ z , I ) x|z\sim\mathcal N(\mu+\Lambda z,I) x ∣ z ∼ N ( μ + Λ z , I ) Diagonal noise ϵ \epsilon ϵ
Example 1.
z ∈ R , x ∈ R 2 , d = 1 , n = 2 , m = 7 z\in\mathbb R,x\in\mathbb R^2,d=1,n=2,m=7 z ∈ R , x ∈ R 2 , d = 1 , n = 2 , m = 7 and z ∼ N ( 0 , 1 ) z\sim\mathcal N(0,1) z ∼ N ( 0 , 1 )
(Source: https://youtu.be/tw6cmL5STuY?t=49m42s )
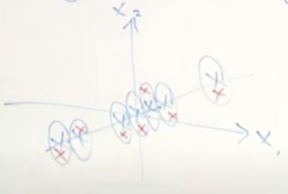
Say Λ = [ 2 1 ] , μ = [ 0 0 ] , Λ z + μ ∈ R 2 , Ψ = [ 1 0 0 2 ] \Lambda=\begin{bmatrix}2\\1\end{bmatrix}, \mu=\begin{bmatrix}0\\0\end{bmatrix},\Lambda z+\mu\in\mathbb R^2,\Psi=\begin{bmatrix}1&0\\0&2\end{bmatrix} Λ = [ 2 1 ] , μ = [ 0 0 ] , Λ z + μ ∈ R 2 , Ψ = [ 1 0 0 2 ]
The red crosses here are a typical sample drwan from this model.
Example 2.
z ∈ R 2 , x ∈ R 3 , d = 2 , n = 2 , m = 5 z\in\mathbb R^2,x\in\mathbb R^3,d=2,n=2,m=5 z ∈ R 2 , x ∈ R 3 , d = 2 , n = 2 , m = 5
(Source: https://youtu.be/tw6cmL5STuY?t=52m16s ; cool animation 😀)
Compute Λ z + μ \Lambda z+\mu Λ z + μ
Factor analysis can take very high dimensional data, e.g., 100 dimensional data.
Multivariate Gaussian
x = [ x 1 x 2 ] x=\begin{bmatrix}x_1\\x_2\end{bmatrix} x = [ x 1 x 2 ] where
x 1 ∈ R r , x 2 ∈ R s , x ∈ R r + s . x_1\in\mathbb R^r,x_2\in\mathbb R^s,x\in\mathbb R^{r+s}. x 1 ∈ R r , x 2 ∈ R s , x ∈ R r + s . x ∼ N ( μ , Σ 2 ) x\sim\mathcal N(\mu,\Sigma^2) x ∼ N ( μ , Σ 2 ) where
μ = [ μ 1 μ 2 ] , Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] . \mu=\begin{bmatrix}\mu_1\\\mu_2\end{bmatrix},\Sigma=\begin{bmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{bmatrix}. μ = [ μ 1 μ 2 ] , Σ = [ Σ 1 1 Σ 2 1 Σ 1 2 Σ 2 2 ] . Marginal: p ( x 1 ) = ? p(x_1)=? p ( x 1 ) = ?
p ( x ) = p ( x 1 , x 2 ) p(x)=p(x_1,x_2) p ( x ) = p ( x 1 , x 2 ) ∫ x 2 p ( x 1 , x 2 ) d x 2 = p ( x 1 ) p ( x 1 , x 2 ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x 1 − μ 1 x 2 − μ 2 ) T ( Σ 11 Σ 12 Σ 21 Σ 22 ) − 1 ( x 1 − μ 1 x 2 − μ 2 ) ) \int_{x_2}p(x_1,x_2)dx_2=p(x_1)\\p(x_1,x_2)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}\begin{pmatrix}x_1-\mu_1\\x_2-\mu_2\end{pmatrix}^T\begin{pmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{pmatrix}^{-1}\begin{pmatrix}x_1-\mu_1\\x_2-\mu_2\end{pmatrix}\right) ∫ x 2 p ( x 1 , x 2 ) d x 2 = p ( x 1 ) p ( x 1 , x 2 ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 exp ( − 2 1 ( x 1 − μ 1 x 2 − μ 2 ) T ( Σ 1 1 Σ 2 1 Σ 1 2 Σ 2 2 ) − 1 ( x 1 − μ 1 x 2 − μ 2 ) ) Conditional: p ( x 1 ∣ x 2 ) = ? p(x_1|x_2)=\;? p ( x 1 ∣ x 2 ) = ?
x 1 ∣ x 2 ∼ N ( μ 1 ∣ 2 , Σ 1 ∣ 2 ) μ 1 ∣ 2 = μ 1 + Σ 12 Σ 22 − 1 ( x 2 − μ 2 ) Σ 1 ∣ 2 = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 x_1|x_2\sim\mathcal N(\mu_{1|2},\Sigma_{1|2})\\\mu_{1|2}=\mu_1+\Sigma_{12}\Sigma^{-1}_{22}(x_2-\mu_2)\\\Sigma_{1|2}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21} x 1 ∣ x 2 ∼ N ( μ 1 ∣ 2 , Σ 1 ∣ 2 ) μ 1 ∣ 2 = μ 1 + Σ 1 2 Σ 2 2 − 1 ( x 2 − μ 2 ) Σ 1 ∣ 2 = Σ 1 1 − Σ 1 2 Σ 2 2 − 1 Σ 2 1 Derive p ( x , z ) p(x,z) p ( x , z )
( z x ) ∼ N ( μ x , z , Σ ) z ∼ N ( 0 , I ) x = μ + Λ z + ϵ \begin{pmatrix}z\\x\end{pmatrix}\sim\mathcal N(\mu_{x,z},\Sigma)\\z\sim\mathcal N(0,I)\\x=\mu+\Lambda z+\epsilon ( z x ) ∼ N ( μ x , z , Σ ) z ∼ N ( 0 , I ) x = μ + Λ z + ϵ E z = 0 E x = E [ μ + Λ z + ϵ ] = μ \mathbb Ez=0\\\mathbb Ex=\mathbb E[\mu+\Lambda z+\epsilon]=\mu E z = 0 E x = E [ μ + Λ z + ϵ ] = μ
μ x , z = [ 0 μ ] ↕ d − dim ↕ n − dim Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] d n = [ E ( z − E z ) ( z − E z ) T E ( z − E z ) ( x − E x ) T E ( x − E x ) ( z − E z ) T E ( x − E x ) ( x − E x ) T ] \begin{aligned}\mu_{x,z}&=\begin{bmatrix}0\\\mu\end{bmatrix}\begin{matrix}\updownarrow d-\text{dim}\\\updownarrow n-\text{dim}\end{matrix}\\\Sigma&=\begin{bmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{bmatrix}\\&\;\;\;\;\;\;\;\;d\;\;\;\;\;\;\;n\\&=\begin{bmatrix}\mathbb E(z-\mathbb Ez)(z-\mathbb Ez)^T&\mathbb E(z-\mathbb Ez)(x-\mathbb Ex)^T\\\mathbb E(x-\mathbb Ex)(z-\mathbb Ez)^T&\mathbb E(x-\mathbb Ex)(x-\mathbb Ex)^T\end{bmatrix}\end{aligned} μ x , z Σ = [ 0 μ ] ↕ d − dim ↕ n − dim = [ Σ 1 1 Σ 2 1 Σ 1 2 Σ 2 2 ] d n = [ E ( z − E z ) ( z − E z ) T E ( x − E x ) ( z − E z ) T E ( z − E z ) ( x − E x ) T E ( x − E x ) ( x − E x ) T ] E.g.,
Σ 22 = E ( x − E x ) ( x − E x ) T = E [ ( Λ z + μ + ϵ − μ ) ( Λ z + μ + ϵ − μ ) T ] = E [ Λ z z T Λ T + Λ z ϵ T + ϵ z T Λ T + ϵ ϵ T ] ( E [ ϵ ] = 0 = E [ ϵ T ] ) = E [ Λ z z T Λ T ] + E [ ϵ ϵ T ] = Λ E [ z z T ] Λ T + Ψ = Λ Λ T + Ψ ( ∵ z ∼ N ( 0 , I ) ) . \begin{aligned}\Sigma_{22}&=\mathbb E(x-\mathbb Ex)(x-\mathbb Ex)^T\\&=\mathbb E[(\Lambda z+\mu+\epsilon-\mu)(\Lambda z+\mu+\epsilon-\mu)^T]\\&=\mathbb E[\Lambda zz^T\Lambda^T+\Lambda z\epsilon^T+\epsilon z^T\Lambda^T+\epsilon\epsilon^T]\\&\;\;\;\;(\mathbb E[\epsilon]=0=\mathbb E[\epsilon^T])\\&=\mathbb E[\Lambda zz^T\Lambda^T]+\mathbb E[\epsilon\epsilon^T]\\&=\Lambda\mathbb E[zz^T]\Lambda^T+\Psi\\&=\Lambda\Lambda^T+\Psi\;(\because z\sim\mathcal N(0,I)).\end{aligned} Σ 2 2 = E ( x − E x ) ( x − E x ) T = E [ ( Λ z + μ + ϵ − μ ) ( Λ z + μ + ϵ − μ ) T ] = E [ Λ z z T Λ T + Λ z ϵ T + ϵ z T Λ T + ϵ ϵ T ] ( E [ ϵ ] = 0 = E [ ϵ T ] ) = E [ Λ z z T Λ T ] + E [ ϵ ϵ T ] = Λ E [ z z T ] Λ T + Ψ = Λ Λ T + Ψ ( ∵ z ∼ N ( 0 , I ) ) . Likewise, we can calculate each Σ i j \Sigma_{ij} Σ i j
Σ = [ I Λ T Λ Λ Λ T + Ψ ] . \Sigma=\begin{bmatrix}I&\Lambda^T\\\Lambda&\Lambda\Lambda^T+\Psi\end{bmatrix}. Σ = [ I Λ Λ T Λ Λ T + Ψ ] . [ z x ] ∼ N ( [ 0 μ ] , [ I Λ T Λ Λ Λ T + Ψ ] ) \begin{bmatrix}z\\x\end{bmatrix}\sim\mathcal N\left(\begin{bmatrix}0\\\mu\end{bmatrix},\begin{bmatrix}I&\Lambda^T\\\Lambda&\Lambda\Lambda^T+\Psi\end{bmatrix}\right) [ z x ] ∼ N ( [ 0 μ ] , [ I Λ Λ T Λ Λ T + Ψ ] ) E-step:
Q i ( z ( i ) ) = p ( z ( i ) ∣ x ( i ) ; θ ) Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\theta) Q i ( z ( i ) ) = p ( z ( i ) ∣ x ( i ) ; θ ) z ( i ) ∣ x ( i ) ∼ N ( μ z ( i ) ∣ x ( i ) , Σ z ( i ) ∣ x ( i ) ) z^{(i)}|x^{(i)}\sim\mathcal N(\mu_{z^{(i)}|x^{(i)}},\Sigma_{z^{(i)}|x^{(i)}}) z ( i ) ∣ x ( i ) ∼ N ( μ z ( i ) ∣ x ( i ) , Σ z ( i ) ∣ x ( i ) ) where
μ z ( i ) ∣ x ( i ) = 0 ⃗ + Λ T ( Λ Λ T + Ψ ) − 1 ( x ( i ) μ ) Σ z ( i ) ∣ x ( i ) = I − Λ T ( Λ Λ T + Ψ ) − 1 Λ . \mu_{z^{(i)}|x^{(i)}}=\vec0+\Lambda^T(\Lambda\Lambda^T+\Psi)^{-1}(x^{(i)}\mu)\\\Sigma_{z^{(i)}|x^{(i)}}=I-\Lambda^T(\Lambda\Lambda^T+\Psi)^{-1}\Lambda. μ z ( i ) ∣ x ( i ) = 0 + Λ T ( Λ Λ T + Ψ ) − 1 ( x ( i ) μ ) Σ z ( i ) ∣ x ( i ) = I − Λ T ( Λ Λ T + Ψ ) − 1 Λ . M-step:
Q i ( z ( i ) ) = 1 ( 2 π ) d / 2 ∣ Σ z ( i ) ∣ x ( i ) ∣ 1 / 2 exp ( − 1 2 ( z ( i ) − μ z ( i ) ∣ x ( i ) ) Σ z ( i ) ∣ x ( i ) − 1 ( z ( i ) − μ z ( i ) ∣ x ( i ) ) T ) Q_i(z^{(i)})=\frac{1}{(2\pi)^{d/2}|\Sigma_{z^{(i)}|x^{(i)}}|^{1/2}}\exp\left(-\frac{1}{2}(z^{(i)}-\mu_{z^{(i)}|x^{(i)}})\Sigma_{z^{(i)}|x^{(i)}}^{-1}(z^{(i)}-\mu_{z^{(i)}|x^{(i)}})^T\right) Q i ( z ( i ) ) = ( 2 π ) d / 2 ∣ Σ z ( i ) ∣ x ( i ) ∣ 1 / 2 1 exp ( − 2 1 ( z ( i ) − μ z ( i ) ∣ x ( i ) ) Σ z ( i ) ∣ x ( i ) − 1 ( z ( i ) − μ z ( i ) ∣ x ( i ) ) T ) ∫ z ( i ) Q i ( z ( i ) ) z ( i ) d z ( i ) = E z ( i ) ∼ Q i [ z ( i ) ] = μ z ( i ) ∣ x ( i ) \begin{aligned}\int_{z^{(i)}}Q_i(z^{(i)})z^{(i)}dz^{(i)}&=\mathbb E_{z^{(i)}\sim Q_i}[z^{(i)}]\\&=\mu_{z^{(i)}|x^{(i)}}\end{aligned} ∫ z ( i ) Q i ( z ( i ) ) z ( i ) d z ( i ) = E z ( i ) ∼ Q i [ z ( i ) ] = μ z ( i ) ∣ x ( i ) θ : = arg max θ ∑ i ∫ z ( i ) Q i ( z ( i ) ) log p ( x ( i ) , z ( i ) ) Q i ( z ( i ) ) d z ( i ) = arg max θ ∑ i E z ( i ) ∼ Q i [ log p ( x ( i ) , z ( i ) ) Q i ( z ( i ) ) ] . \begin{aligned}\theta:&=\argmax_\theta\sum_i\int_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)})}{Q_i(z^{(i)})}dz^{(i)}\\&=\argmax_\theta\sum_i\mathbb E_{z^{(i)}\sim Q_i}\left[\log\frac{p(x^{(i)},z^{(i)})}{Q_i(z^{(i)})}\right].\end{aligned} θ : = θ a r g m a x i ∑ ∫ z ( i ) Q i ( z ( i ) ) log Q i ( z ( i ) ) p ( x ( i ) , z ( i ) ) d z ( i ) = θ a r g m a x i ∑ E z ( i ) ∼ Q i [ log Q i ( z ( i ) ) p ( x ( i ) , z ( i ) ) ] . Plug in Gaussian density to numerator and denominator, respectively.