Kaggle: Comprehensive data exploration with Python

해당 글은 Kaggle에 작성된 포스트를 기반으로 작성하였습니다.

해당글에서 다루는 문제는 집에 대한 정보(집 가격, 집 방의 개수, 집의 면적 등)를 이용하여 집의 가격을 예측하는 것입니다.

이번 글에서는 주택의 정보(데이터)를 분석해보겠습니다. (정보를 분석하여 해당 정보를 어떻게 머신러닝 모델에 적용할 것인지 결정하기 위함이라 생각합니다.)

데이터 불러오기

구글 코랩에서 진행했기 때문에 데이터를 불러오려면 드라이브와 코랩을 마운트해야합니다.

from google.colab import drive
drive.mount('/content/drive')

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

마운트 후에 csv 파일을 읽어드립니다. (pandas를 이용)
파일 경로를 유심히 보시고 각자의 상황에 맞게 경로를 변경하시면 될 것 같습니다.

df_train = pd.read_csv('/content/drive/My Drive/colab/Kaggle_Data_Analysis/train.csv')

1. So... What can we expect?

데이터의 각 feature를 살펴보는 것은 상당히 시간이 걸리는 일입니다.

feature를 살펴 본다는 의미는 각 feature의 의미 혹은 문제와의 관련성을 이해하겠다는 것입니다.

각 feature를 시각화 하는 방법(scatter plot, bar graph 등)에 따라 feature에 대한 우리의 결론이 달라질 수 있습니다. $\rarr$ 즉 각 데이터의 의미에 따라 적절한 시각화를 진행해야 하는 것으로 이해했습니다

2. First things first: analysing 'SalePrice'

아래 코드는 주택 가격의 분포 시각화를 위한 코드입니다.

sns.distplot(df_train['SalePrice'])

아래 코드는 분포의 특성을 보여주는 코드입니다. (저도 의미는 잘 모르겠습니다. 차차 알아가야할 듯합니다.)

# skewness and kurtosis
df_train['SalePrice'].skew()
df_train['SalePrice'].kurt()

'SalePrice', her buddies and her interests

Relationship with numerical variables

아래 코드는 GrLivArea 값과 SalePrice의 관계를 시각적으로 보여줍니다. (각각 X축, Y축)

직접 실행시켜 눈으로 확인해주세요!

# scatter plot GrLivArea/SalePrice
var = 'GrLivArea'
data= pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))

아래 코드는 TotalBsmtSF와 SalePrice의 관계를 보여줍니다.

# scatter plot TotalBsmtSF/SalePrice
var = 'TotalBsmtSF'
data= pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))

Relationship with categorical features

OverallQual과 SalePrice의 관계를 살펴봅시다.

# box plot OverallQual/SalePrice
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000)

YearBuilt와 SalePrice의 관계를 살펴봅시다.

var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000)
plt.xticks(rotation=90)

간단한 데이터 분석 요약

GrLivArea & TotalBsmtSF는 SalePrice와 선형관계인 듯하다.

• 두 fetures 모두 주택가격과 positive한 관계이다.

• 기울기는 feature에 따라 다르다.

OverallQual & YearBuilt 역시 주택가격과 관계가 있는 듯해보인다.

• YearBuilt의 경우 중간중간에 주택가격이 튀는 부분이 있다.

• OverallQual의 경우 YearBuilt보다는 스무스하게 주택가격과 상관이 있는 듯하다.

3. Keep calm and work smart

지금까지 직관을 중심으로 데이터를 분석했습니다. (제가 생각해도 그렇네요.)

이제부터 주관적인 생각을 빼고 조금 더 객관적으로 데이터를 분석할 것 같습니다.

The plasma soup

Correlation matrix (heatmap style)

아래 코드는 변수간의 관계를 시각화 해주는 코드입니다.

# correlation matrix
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True)

sns.heatmap을 통해서 correlation matrix를 시각화하면 변수간의 상관관계를 빠르게 파악할 수 있습니다.

• 주어진 데이터의 heatmap을 그리면 faeture간에 상관관계가 높은 feature 쌍을 확인할 수 있습니다. $\rarr$ multicollinearity

• multicollinearity(다중공신성): 다중공신성 특징을 가지는 feature가 있을 경우 부정확한 회귀결과가 도출됩니다.

• heatmap 시각화해서 이러한 특징을 가지는 feature들을 파악하여 feature selection을 진행할 수 있습니다.

• 또한 우리는 주택가격을 예측하는 모델을 만들고 싶은 것이기에 SalePrice column 또는 row를 확인하여 주택가격과 상관관계가 높은 feature를 파악할 수 있습니다.

'SalePrice' correlation matrix (zoomed heatmap style)

# SalePrice correlation matrix
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(
    cm, 
    cbar=True, 
    annot=True, 
    square=True, 
    fmt='.2f', 
    annot_kws={'size': 10}, 
    yticklabels=cols.values, 
    xticklabels=cols.values
    )
plt.show()

위 코드를 실행하면 SalePrice와 높은 상관관계를 가지는 상위 10개(SalePrice 포함) features의 correlation matrix를 heatmap으로 표현합니다.

• 코드를 실행하면 GarageCars와 GarageArea features도 볼 수 있습니다.

• 그런데 위 두 features는 서로 상관관계가 정말 높습니다.

  • GarageCars: 차를 몇대 수용하는지 나타냅니다.

  • GarageArea: 차고의 면적을 나타냅니다.

• features 간의 상관관계가 높은 경우 한개만 선택하면 됩니다.

  • 위의 경우 GarageCars 가 주택가격과 상관관계가 더 높으므로 GarageCars를 feature로 선택합니다.

• YearBuilt 또한 주택가격과 상관관계가 다소 있습니다.

  • 그런데 집이 언제 지어졌는지(YearBuilt)와 주택가격은 경제 관점에서 보면 inflation 때문에 어느정도 상관관계가 있는 것이 맞는것으로 생각됩니다.

  • 그렇다면 우리는 인플레이션도 고려해야 할까요...?

Scatter plot between 'SalePrice' and correlated variables (move-like Jagger style)

# Scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show()

위 코들 실행하면 자기 자신을 제외한 다른 feature와의 scatter plot을 보여줍니다.
위의 경우 feature 7개가 있으므로 총 36개의 그래프가 그려지겠네요.

그래프를 통해서 feature 간의 의미를 파악해보세요.

4. Missing data

# missing data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

위 코드를 실행하면 각 feature에 대해서 해당 feature가 null인 개수('Total') & 전체 샘플중 null이 차지하는 비율('Percent')을 확인할 수 있습니다.

우리는 feature의 Missing data 비율이 15% 이상이라면 해당 feature를 사용하지 않겠습니다.
(해당 feature들은 주택가격에 영향을 미치는 정도가 매우 적습니다. 그래서 Missing data 비율이 높은 것일지도 모르겠네요.)

15%가 되지 않는 것중에서도 없앨 features가 있습니다.
(GarageX: GarageCond, GarageType, ..., etc)
그런데 주차장과 관련된 features의 경우 GarageCars feature가 주택가격과 상관관계가 높으므로 GrageX에 속하는 features는 없애도록 하겠습니다. (같은 이유로 BsmtX도 없앱니다.)

또한 MasVnrArea는 OverallQual과 상관관계가 높고 MasVnrType은 OverallQual와 상관관계가 높으므로 둘다 제거합니다. (Missing data 비율이 적긴하나 어쨌든 데이터 손실도 있긴하니까...)

• 블로그에는 이렇게 써있는데 궁금해서 직접 눈으로 확인해보려했습니다.

• 아래는 코드입니다.

selected_features = ['MasVnrArea', 'MasVnrType', 'YearBuilt', 'OverallQual']
corrmat = df_train[selected_features].corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmin=-0.8, vmax=.8, square=True)

• 아래는 결과 이미지입니다.

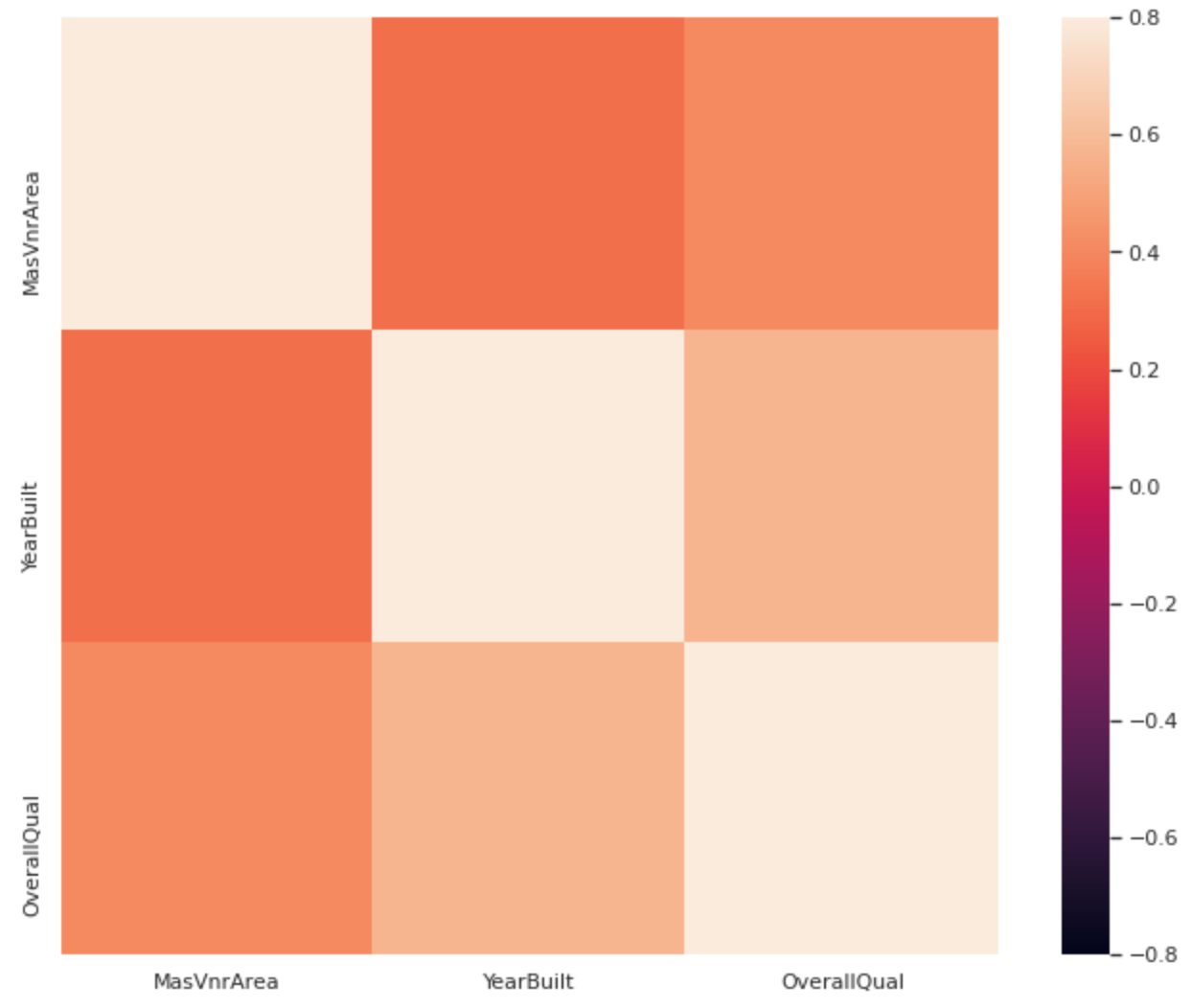
• MasVnrArea는 OverallQual과 상관관계가 꽤나 있어보이네요.

• 보시면 알겠지만 MasVnrType feature는 없습니다. (제 개인적인 생각으로 카테고리 feature라서 그런게 아닐까 조심히 생각해봤습니다.)

• 따라서 MasVnrType feature와 YearBuilt & OverallQual feature와의 상관관계를 boxplot을 활용했습니다.

# 'YearBuilt'만 'OverallQual'로 변경 가능
var = 'MasVnrType'
data = pd.concat([df_train['YearBuilt'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="YearBuilt", data=data)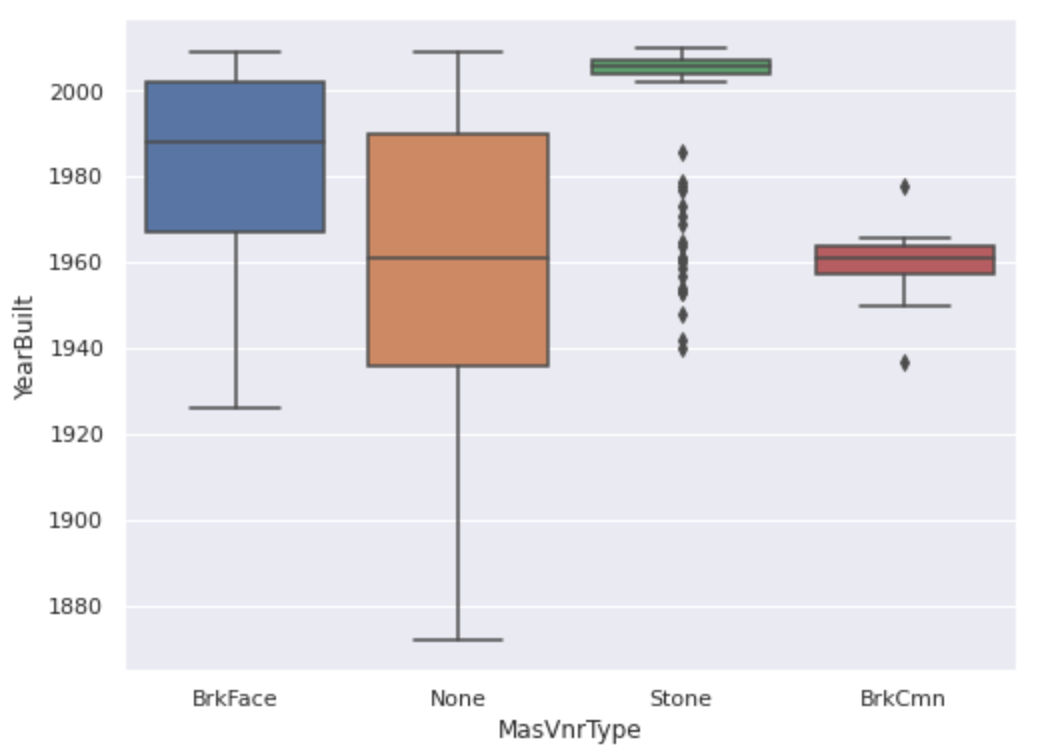

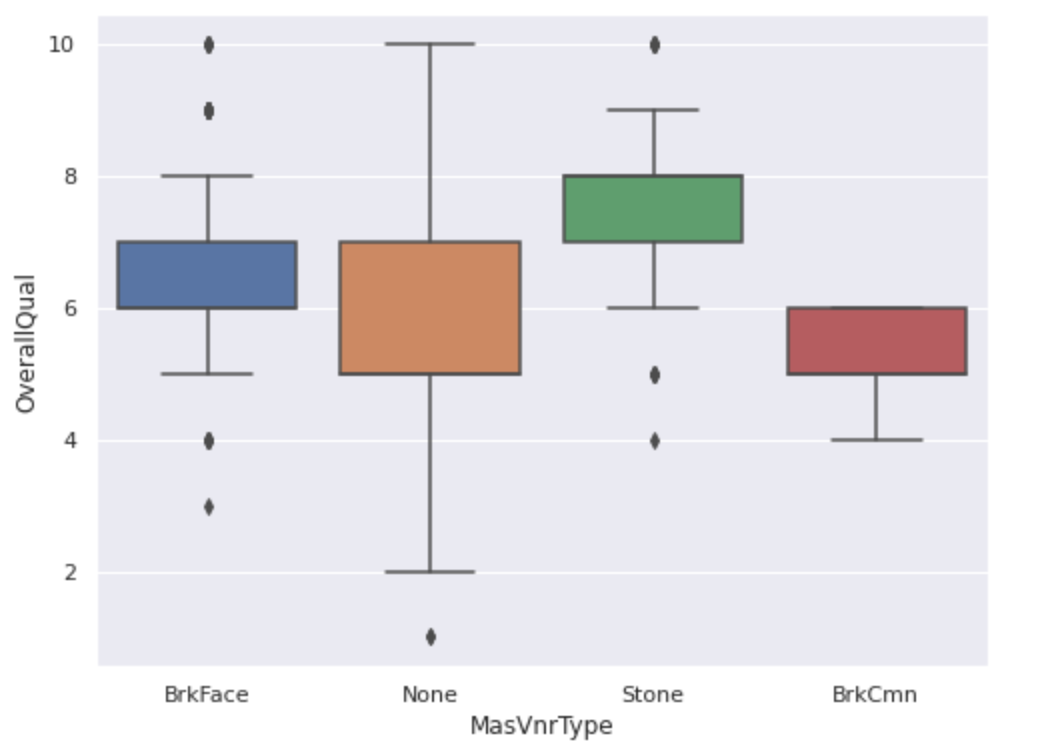
(상관관계가 깊어 보이나요? boxplot에 대해서 아직 정확하게는 몰라서 해석을 완벽하게 할 순 없네요 ㅜ)

Missing data를 직접 코드로 확인해 보셨다면 Electrical feature도 Missing data 1개가 존재한다는 것을 알 수 있습니다.

이경우에는 observation(샘플 혹은 sample, data 1개)이 1개이므로 그 샘플을 지웁니다. (코드는 아래와 같습니다.)

# 위에서 제거하기로 했던 features 제거
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index, 1)

# 샘플 1개 삭제
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)

# checking there's no missing data
df_train.isnull().sum().max()

Out liars!

Outliers는 우리가 개발하고자 하는 모델에 눈에 띄는 영향을 미칠 수 있습니다.

SalePrice 표준 편차를 활용하여 간단하고 빠른 분석을 해봅시다.

우리는 최우선 적으로 threshold 를 정해야합니다. 무슨 threshold 이냐면 관찰된 부분이 outlier 인지 아닌지 판별할 때 사용할 threshold 입니다.

Univariate analysis

Threshold 를 정하기 위해 데이터를 표준화 할 것입니다.
(이 글에서 데이터 표준화의 의미는 데이터를 평균이 0 & 표준 편차가 1이 되도록 변환하는 것입니다.)

# Standardizing data
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:, np.newaxis])
low_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][:10]
high_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

Bivariate analysis

우리는 위에서 SalePrice 와 GrLivArea 의 관계를 분석했습니다.

두 변수를 scatter 로 표현했을 때 데이터의 집합 중에서 전체적인 경향성을 따라가지 않는 두점이 있습니다. (GrLivArea 값이 너무 큰 경우였습니다. 해당 경우는 농경지역이라 생각할 수 있고 집의 면적이 넓더라도 집 가격이 많이 비싸지 않은 경우입니다.)

경향성을 따라가지 않는 2 데이터를 outliers 로 정하고 해당 데이터를 삭제하도록 하겠습니다.

# Deleting points
df_train.sort_values(by='GrLivArea', ascending=False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)

데이터 2개를 삭제 후 다시 scatter 를 그려보면 해당 데이터가 삭제되어 전체적으로 데이터의 경향성이 더 잘 드러남을 볼 수 있습니다.

이런 식으로 데이터들의 전체적인 경향성을 무시하는 데이터들이 있을 것입니다.

그런 데이터들을 삭제하고 훈련을 시킨다면 더 괜찮은 모델이 될 수 있지 않을까요? (필자 생각입니다...)

5. Getting hard core

이번에는 Multivariate analysis 를 해봅시다.

Multivariate techniques 을 적용하기 위해 SalePrice 가 어떤 통계 가정을 가지고 있는지 이해해보겠습니다.

• Normality: 데이터가 Normal Distribution 을 따라야합니다. 몇몇 통계 테스트는 Normal Distribution 일 때 가능합니다. (따라서 중요...!)

• Homoscedasticity: 독립 변수(feature)는 종속 변수에 대해서 동일한 편차를 가져야 하는 가정입니다.

• Linearity: Linear는 선형 관계를 의미합니다. 선형 관계가 아니라면 data transformations 을 활용해야합니다. (현재 이 글에서 다루고 있는 데이터는 모두 선형 관계를 보이고 있습니다.)

• Absence of correlated errors: 예를 들어 어떤 종속 변수 2개가 서로 관련이 있다고 해봅시다. 하나의 종속 변수 때문에 에러가 생겼다면 반대로 다른 하나의 종속 변수 때문에도 에러가 발생할 것입니다. (서로 correlated 하기 때문이죠.)

In the search for normality

• History: Kurtosis & skewness

• Normal Probability plot: Data distribution은 normal distribution을 의미하는 대각선과 비슷해야 합니다.

# Histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

해당 코드를 실행하여 확인해보면 우리가 가지고 있는 데이터는 peakedness, positive skewness 특징을 보여줍니다. 또한 normal distribution을 따르지 않는 것을 확인할 수 있습니다.

하지만 simple data transformation 으로 위의 문제를 해결할 수 있습니다. (positive skewness 의 경우 log transformations으로 해결 가능합니다.)

# applying log transformation
df_train['SalePrice'] = np.log(df_train['SalePrice'])

# transformed histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

위 코드의 실행결과를 보면 data transformations 의 강력한 결과를 확인할 수 있습니다..! (위의 과정을 GrLivArea feature 에도 수행하면 되겠습니다!)

TotalBsmtSF feature에 대해서도 distribution 과 probplot을 수행해보세요. (결과를 보면 data tranformations 을 어떻게 적용해야할지 난감합니다. 저 같은 초보자 입장에서...)

결과를 조금 분석해보자면 TotalBsmtSF 값이 0인 데이터의 분포가 normal distribution 을 따르지 않습니다. (값이 0인 데이터가 너무 많습니다.)

TotalBsmtSF 에 log transformation 을 적용하기 위해 HasBsmt 변수를 만들겠습니다.

HasBsmt 변수는 basement 를 가지고 있다면 1 가지고 있지 않다면 0 값을 가집니다. 그리고 해당 변수 값이 1인 데이터들에 대하여 log trasformation 을 적용하고 그래프를 그려봅시다.

# create column for new variable (one is enough because it's a binary categorical feature)
# if area > 0 it gets 1, for ares == 0 it gets 0
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0
df_train.loc[df_train['TotalBsmtSF']>0, 'HasBsmt'] = 1

# transform data
df_train.loc[df_train['HasBsmt']==1, 'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])

# histogram and normal probability plot
sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)

(결과를 확인해보면 완벽하진 않지만 어느정도 normal distribution & linerity 한 것을 볼 수 있습니다.)

In the search for writing 'homoscedasticity' right at the first attempt

Homoscedasticity 를 테스트하는 가장 좋은 방법은 시각화하여 눈으로 확인하는 것입니다.

분산이 일정하지 않다면 그래프의 모양이 cones 혹은 diamonds 입니다.

• cones: 분산이 작은 부분은 좁고 반대쪽은 분산이 커서 넓은 모양

• diamonds: 분포의 가운데에 많은 데이터들이 몰려서 생기는 모양

SalePrice & GrLivArea 를 시각화해서 확인해봅시다.

plt.scatter(df_train['GrLivArea'], df_train['SalePrice'])

plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice'])

확인해보면 초기의 그래프와 nomality 를 적용한 그래프의 모양이 달라졌음을 아래와 같이 확인할 수 있습니다. (그림 첨부, 실제 그래프는 코드 작성 후 직접 확인해보세요! :-)

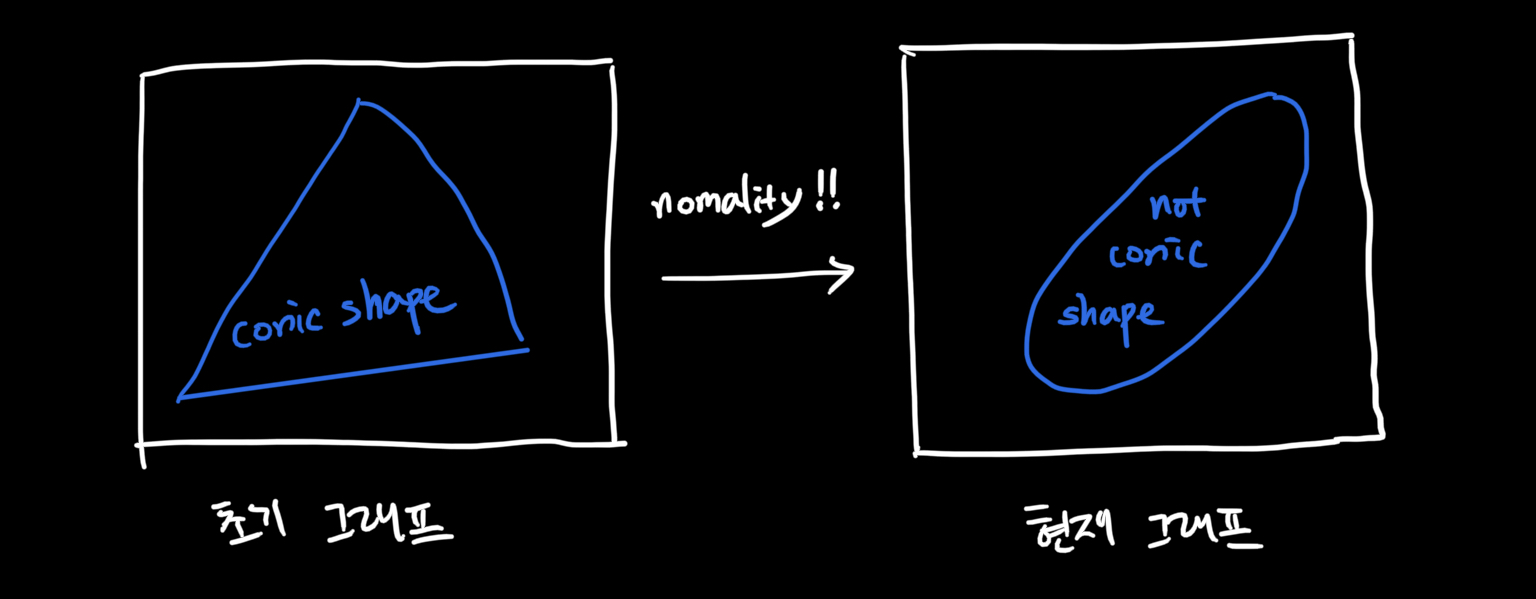
Conclusion

우리는 변수들을 분석하는 방법들에 대해 배웠습니다.

• Correlated 변수들을 활용하여 SalePrice 변수를 분석했습니다.

• Missing data & outliers 를 다루었습니다.

• The fundmental statistical assumptions (이전에 언급되었던 4가지 항목) 을 테스트 했습니다. (log transformation 활용)