1. 12강 복습
12강에서는 Visualization을 다루며 다양한 layer의 filter들을 시각화했었다. 첫 번째 layer의 filter들에서는 대체적으로 oriented edge를 찾는 경향을 보였고, intermediate layer들의 filter들에서는 의미 있는 결과를 보지 못했다. 마지막 layer에서는 나름 의미 있는 결과가 나왔다. 이때 모호한 intermediate layer filter들에 대해 자세히 이해하기 위해 feature map을 출력해보기로 했다. 여러 가지 method들을 통해 feature들이 뭘 배우려고 했는지 알 수 있었다.
이번 강의에서는 training data를 이용해 그와 비슷하지만 새로운 image를 생성하는 Generative Model에 대해 배운다.
2. Supervised Learning VS Unsupervised Learning
1) Supervised Learning
Supervised Learning은 data와 label을 가지고 training을 진행하는 것이다. data를 (x,y)라고 하자. 여기서 x는 data, y는 label이다. Supervised learning에서는 x->y 를 표현하는 수식을 mapping하는 것이 가장 큰 목표다. Supervised Learning의 예시로는 classification, regression, object detection, semantic segmentation, image captioning 등이 있다.
2) Unsupervised Learning
Unsupervised Learning이 supervised learning과 가장 다른 점은 label이 없다는 것이다. label없이 내 data에 숨어 있는 특정한 구조(hidden structure)를 찾는 것이다. label이 없기 때문에 training data에 드는 비용이 적다. 예시로는 clustering, dimensionality reduction, feature learning, density estimation이 있다.
i) Clustering: 특성이 비슷한 데이터끼리 묶어주는 것을 말한다.
ii) Dimensionality Reduction: 말 그대로 차원 축소를 말한다. 데이터를 잘 설명해주는 feature들을 선택하고, 그것을 기반으로 차원을 축소하는 것이다. 대표적인 방법으로 PCA(Principle Component Analysis)이 있다.
iii) Feature Learning: 강의 후반에 나오는 AutoEncoder에 사용된다. 후반에 가서 자세히 설명하겠다.
iv) Density Estimation: 데이터에 기반해서 변수에 대한 밀도를 예측하는 것이다. 여기서 밀도는 확률 밀도함수에서 나오는 밀도라고 생각하면 된다.
3. Generative Model의 개요
Training data가 주어졌을 때, 같은 분포(distribution)에서 새로운 sample들을 생성하는 모델들을 통틀어 generative model이라고 한다.

위의 사진과 같이 training data가 주어졌을 때, data x의 분포를 p_data(x), 모델이 만든 sample들의 분포를 p_model(x)라고 한다. Generative Model의 목표는 p_data(x)와 p_model(x)를 최대한 비슷하게 하는 것이다. 두 분포가 비슷하다면, training data와 비슷한 sample들이 만들어질 것이기 때문이다. 이 목표를 듣고 자연스럽게 드는 생각이 '어떻게 분포를 예측할 것인가?'이다. 즉, density estimation을 잘해야 모델의 좋은 성능을 얻을 수 있다는 뜻이다. 실제로 이는 unsupervised learning에서 해결해야 할 주요 과제 중 하나라고 한다. Generative Model은 Explicit Density Estimation 혹은 Implicit Density Estimation 중 하나를 이용해서 만든다. 전자는 p_model(x)를 직접 정의하고 그에 대해 문제를 해결하는 방식이고, 후자는 p_model(x)를 직접적으로 정의하지 않고 sampling을 할 수 있는 모델을 만드는 방식이다.
이제 대략적으로 Generative Model이 무엇인지 정도는 알았다. 그렇다면 이것을 왜 만든 것일까? 이 모델을 이용하면 다양한 분야에서 사용할 수 있는 사실적인 사진들을 얻을 수 있다. 미술 작품, Super Resolution, Colorization 등의 과제들에 이용될 수 있다. 또, 일정한 시간 간격으로 배치된 데이터들의 수열을 의미하는 time-series(시계열) data에 이 모델을 적용할 경우, simulation과 planning에 이용될 수 있다고 한다.(planning은 이후에 reinforcement learning에서 자세히 다룰 예정이라고 한다.) 마지막으로, generative model들을 훈련시키면 나중에 general feature로 이용할 수 있다.
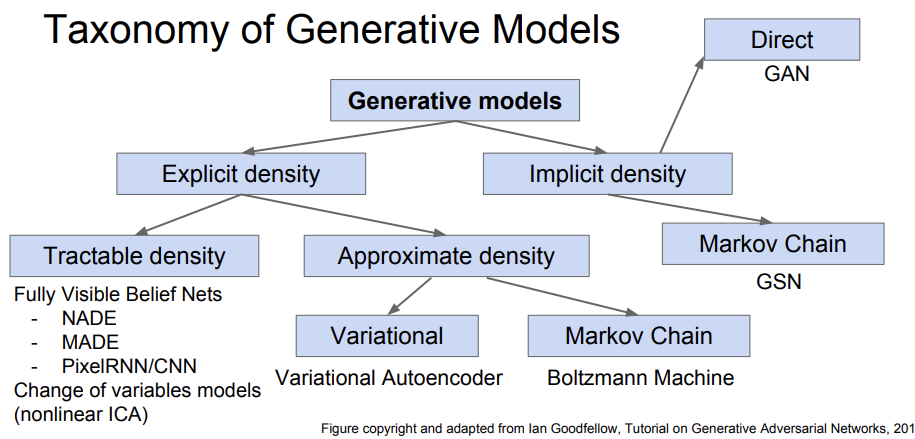
강의는 위의 Generative Model 중 가장 대표적인 모델 3개인 Pixel RNN/CNN, Variational Autoencoder, GAN을 다룬다.
4. Pixel RNN & PixelCNN
1) Fully Visible Belief Network(FVBN)
Explicit Density Network 중에 하나로, chain rule을 이용해서 input 이미지 x의 likelihood를 decompose한다. 그 결과, 1d distribution을 얻게 된다. 바로 뒤에 소개할 PixelRNN/CNN도 모두 FVBN 중의 하나이다.
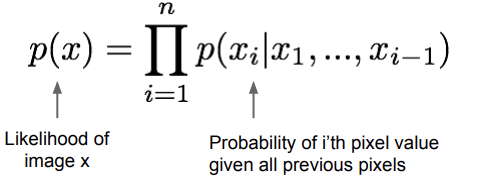
위 식에서 은 각 픽셀의 값을 의미한다. 따라서, 는 previous pixel들이 주어졌을 때 의 확률을 모두 곱한 값이다. 즉, 조건부확률값들을 모든 픽셀에 대해서 다 곱했다고 보면 된다. 여기서 구한 training data의 likelihood를 최대화하는 것이 training의 목표이다. 그러나, 위의 조건부 확률 분포는 표현하기에 다소 복잡해 보인다. 뒤에도 계속 나오지만, 이렇게 복잡한 분포를 만났을 때 neural network를 이용해서 표현한다. 그런데 여기서 하나의 의문점이 생긴다. 앞서 말한 previous pixel은 어떤 기준으로 정할 것인가이다. 이것에 대한 답을 주는게 PixelRNN과 PixelCNN이다.
2) PixelRNN
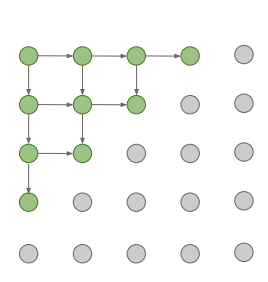
위의 사진은 PixelRNN의 구조도이다. 각 점들은 pixel들을 뜻하는데, 초록색이 previous pixels, 회색이 아직 지나지 못한 픽셀을 의미한다. PixelRNN은 좌상단의 꼭짓점에서 시작해 아래와 오른쪽으로 확장해 나간다. 이러한 기준으로 규칙에 따라 이미 지나온 pixel들이 previous pixel들에 해당한다. 이전 강의에서 살펴봤듯이, RNN, 정확히는 LSTM은 모델 특성상 이전 픽셀들의 영향을 많이 받게 된다. 이 방식의 문제는 sequential generation이기 때문에 생성 속도가 느리다는 것이다. 그래서 도입된 것이 PixelCNN이다.
3) PixelCNN
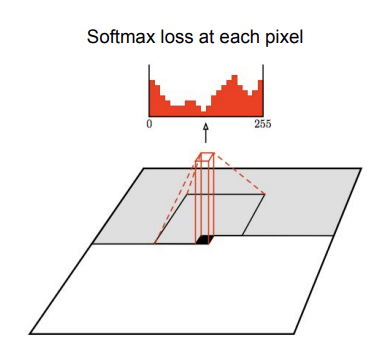
이 방법도 PixelRNN과 같이 하나의 꼭짓점에서 시작한다. 다른 점은 이름에서도 알 수 있듯이, RNN 대신 CNN을 적용했다는 것이다. CNN과 같이, 이미지를 훑으면서 각 pixel을 generate한다. 여기서도 지나온 pixel들이 previous pixel이 된다. 이전 픽셀들을 이용해서 현재 영역을 출력하는 것이다. 이렇게 CNN을 태우면, 각 픽셀은 ground truth training image와의 차이를 계산해 softmax loss 값을 갖게 된다. 이 값의 범위는 보통 0~255이다. 보통 8bit로 사진을 표현하기 때문이다. loss 값을 얻고 나면, 를 최대화하는 방향으로 training을 진행한다. 일반 CNN과 다르게, PixelCNN은 external label 없이 훈련을 진행한다.
이 방법은 모든 ground truth image가 training data를 통해 주어져 있기 때문에 훈련 속도가 PixelRNN보다는 빠르지만, 여전히 sequential genreation이다 보니 생성 속도는 느리다는 단점이 있다.
4) PixelRNN/CNN의 장점
-장점: explicit 하게 p(x)를 계산할 수 있고, training 시의 likelihood도 explicit하게 볼 수 있어 evaluation시에도 좋은 metric을 제공한다.
-단점: sequential generation이기 때문에 생성 속도가 느리다.
5. Variational Autoencoders(VAE)
이제까지는 tractable한 density function을 정의해서 likelihood optimization을 진행했다.
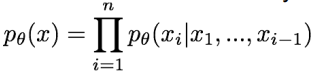
이제부터 살펴볼 VAE는 intractable density function을 정의한다. 이를 위해 latent variable(잠재 변수 정도로 이해하면 될 것 같다.) z를 정의한다.
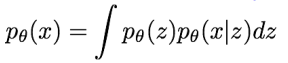
이 식은 직접적으로 optimize 할 수 없다. 그렇기 때문에 lower bound를 잡아 likelihood를 lower bound 이상으로 최적화 시키는 것이다. VAE를 살펴보기 전에, 먼저 Autoencoder가 뭔지부터 알아보자.
1) Autoencoder
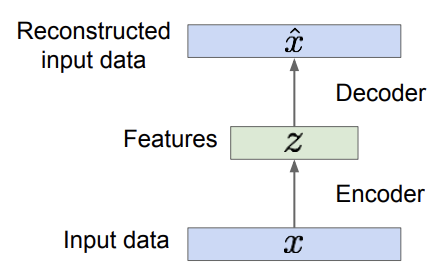
Autoencoder는 encoder와 decoder로 구성된다. encoder는 input data로부터 의미 있는 feature들을 얻는 수식을 mapping하고, decoder는 이렇게 얻은 feature들을 이용해 원래의 input data를 복원한다. feature들은 dimensionality reduction을 해서 데이터의 의미있는 부분들을 포착한다. 이때 label은 존재하지 않고, 그냥 픽셀 값들에 대해서만 복원이 이루어진다. 목표는 original input과 reconstructed data, 즉 x_hat과 x를 최대한 비슷하게 만드는 것이다. 이렇게 훈련이 끝나고 나면, decoder network는 버린다. 그리고 훈련된 feature들을 가진 encoder network를 통해 supervised model을 초기화 할 수 있다.
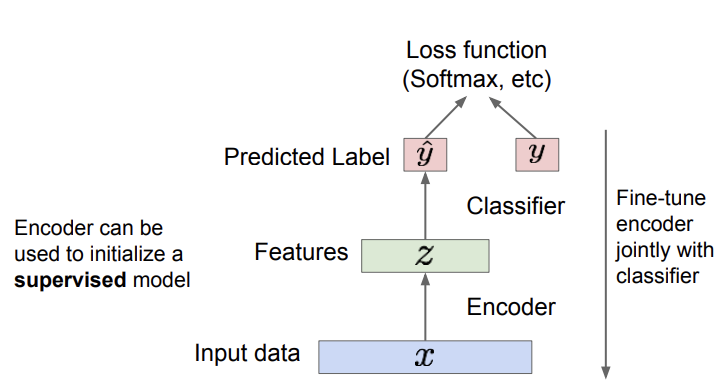
그러면 위의 사진과 같이 encoder network만 이용해 classification을 할 수 있게 된다. features에서 label을 predict하고 ground truth label과 비교해 training 시키는 것은 일반적인 classifier와 그닥 다르지 않다. 여기서 하나의 의문점이 생긴다. 이미 나와있는 supervised model들이 있는데 굳이 이렇게 해야 할까? 이런 방법은 상대적으로 적은 양의 데이터를 가지고 있을 때 유용하다고 한다. 이 아이디어를 이용해 새로운 이미지도 만들 수 있겠다는 생각에서 VAE가 만들어졌다.
2) Variational Autoencoder(VAE)
Autoencoder를 이용해 모델에서 sampling을 하여 새로운 이미지를 생성하는 방법이다.
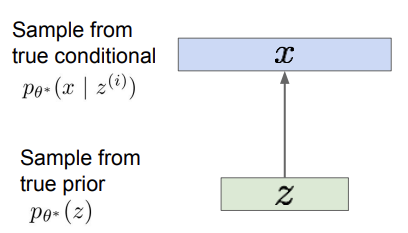
일단, 훈련 데이터가 latent representation인 를 통해 생성되었다고 하자. 는 training data에 대해 variation을 얼마나 가지고 있는지에 대한 정보를 준다. 예를 들어 얼굴 사진을 생성한다고 하면, 는 얼굴이 웃고 있는 정도, 고개의 각도 등의 feature일 것이고, 이런 특성들을 가지고 있는 를 통해 이미지인 를 얻는 것이다. 먼저, prior(사전 확률) 를 sampling 해서 를 얻는다. 는 보통 gaussian 형태로 만든다. 그리고 얻은 분포를 통해 (를 뽑았을 때 의 확률)를 sample 하는 것이다. 이게 말은 쉬워보이지만, 간단한 문제는 아니다. 모델을 훈련시켜 새로운 이미지를 얻으려면, parameter인 를 추정해야 한다.
그렇다면 이 모델을 어떻게 표현해야 할까? 일단 는 간단한 gaussian 분포가 되도록 한다. 그리고 conditional 는 복잡한 분포이기 때문에 앞에서와 같이 neural network를 이용해 표현한다. 정확히는 이 네트워크를 decoder network라고 부른다. 그리고 training 시에는 FVBN에서 사용한 방법을 이용한다.
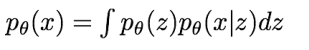
위의 수식은 image에 대한 확률 분포를 나타낸다. 는 latent variable을 의미한다. 여기서도 목적은 를 최대화하도록 모델을 훈련시키는 것이다. 그러나 위에서 언급했듯이, latent 를 이용하기 때문에 intractable하다는 단점이 있다. 위의 식에서, 는 gaussian이고 는 decoder network이니 이 두개의 분포는 tractable하다. 그러나 를 모든 에 대해 계산하는 것, 즉 식에서의 integral은 intractable하다. 때문에 data likelihood term은 intractable 하다. 그렇다면 posterior density는 어떨지 한 번 살펴보자.
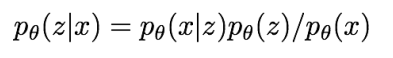
bayes' rule에 의해 posterior density를 위 수식처럼 표현할 수 있다. 가 intractable하므로 도 intractable하다. 이것에 대한 해결책으로 decoder network인 에 추가로 를 근사하는 encoder network 하나를 더 정의한다. 후에 나오겠지만, 이렇게 함으로써 우리는 data likelihood에 대한 lower bound를 얻을 수 있다. lower bound는 최적화를 할 수 있게 해주기 때문에, lower bound를 얻는 것은 중요하다.
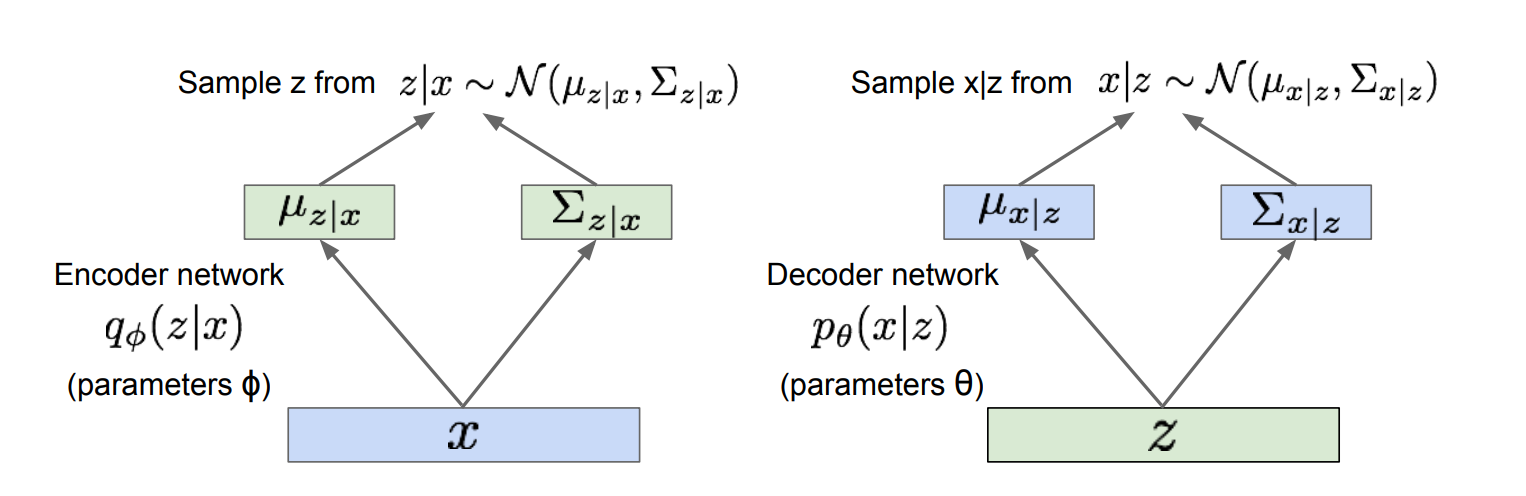
우선, 는 encoder network를 통해 에 대한 평균,분산값을 얻게 된다. 이렇게 얻은 분포에서 를 sampling한다. 그리고 를 decoder network에 태워서 에 대한 평균, 분산을 얻고, 이를 통해 를 sampling한다. 이제 우리가를 계산하기 위해 필요한 값들을 다 얻었다. 구체적인 식은 아래 사진과 같다.
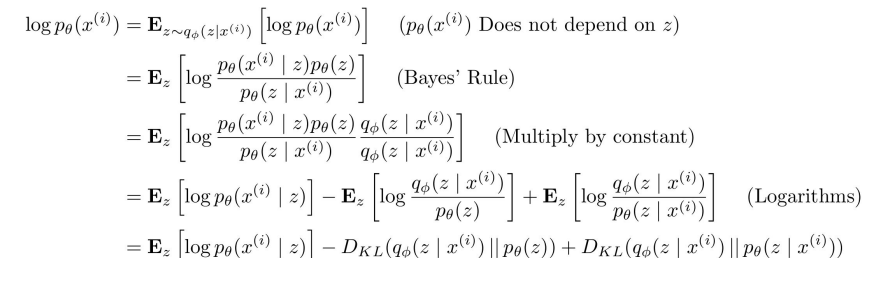
일단 위의 E는 Expectation을 뜻하고, 위의 경우 이라고 적혀있다. 그렇기 때문에 위의 E 값은 encoder network에서 를 sample했을 때의 기댓값을 의미한다고 보면 된다. 구체적인 수식은 다루지 않겠다. 위의 사진의 'multiply by constant'라고 쓰여있는 줄을 살펴보자. 쉽게 말하면 분자와 분모에 같은 상수를 곱한 것이다. 이건 마지막 줄에 KL divergence term을 나타내는데 도움을 준다고 한다. KL divergence는 두 분포의 차이를 계산하는 방법이다. 이제 마지막 줄을 살펴보자.
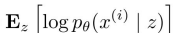
decoder network에서 우리는 를 얻을 수 있다. sampling을 통해 이 term을 추정할 수 있다.
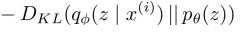
이 KL term은 2개의 gaussian 분포를 다루므로, 계산할 수 있다.
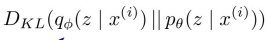
마지막 항이다. 는 앞서 봤듯이 intractable하다. 그러므로 KL term도 계산할 수 없다. 하지만 KL term은 무조건 0 이상이니까 lower bound를 구하는 것은 가능하다.

정리하자면, 구할 수 있는 2개의 term들은 tractable lower bound라고 한다. 이제 에 대한 lower bound를 얻었다. 목표는 이 lower bound를 최대한 높이는 것이다. likelihood가 적어도 lower bound보다는 높을 것이기 때문에, lower bound를 최대한 높이고 최적화 시키는 것이 중요한 일이다.
참고) KL-Divergence는 아래 링크에 자세히 설명해 놓았다.
https://velog.io/@danlee0113/Entropy-Cross-Entropy-KL-Divergence
이제 어떤 식으로 VAE를 최적화시킬지에 대한 방법을 찾았다. 그러면 이제 이걸 어떻게 계산(forward pass)하는지 알아보자.
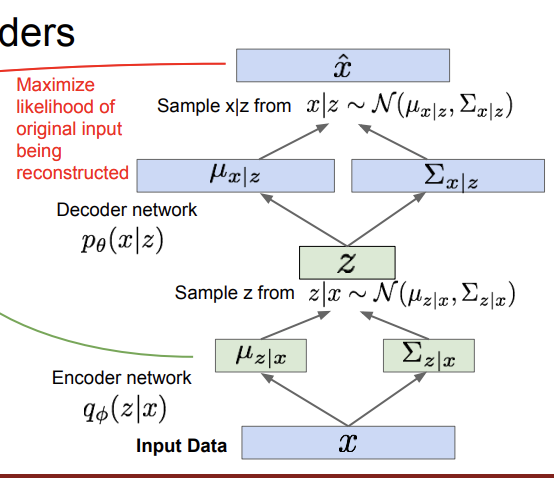
각 mini batch에 대해 위 과정을 진행한다. 위에서 본 과정을 다 합쳐놓은 것이다. 한 번 더 정리해보자. encoder network를 통해 의 분포를 얻고 여기서 를 sampling을 한다. 이 를 decoder network에 태워서 를 얻고, 에서 sampling을 진행한다. 이렇게 얻은 값들로 를 복원한다. 이때 의 likelihood를 최대화 시키는 것이 우리의 목표이다. 여기서 주의할 점은 decoder network에서는 prior 에서 sampling하고, encoder network에서는 posterior 에서 sampling한다는 것이다. 추가로, 의 각각의 다른 차원들은 interpretable한 특성들을 나타낸다고 한다.

위 사진의 경우, 세로 방향은 웃음의 정도를 나타내고, 가로 방향은 머리의 자세를 나타낸다. 이 두 개가 z의 각각의 차원을 나타내는 것이다.

정리하자면, VAE는 genreative model에 대해 규칙을 가지고 접근을 시도했고, 에 대한 inference를 가능하게 해주었다. 이것은 다른 과제들에 대해 유용한 feature representation으로 이용할 수도 있다. 그러나 lower bound를 이용하기 때문에 PixelCNN/RNN보다 좋은 성능을 내진 못하고, 현재 SOTA 기술인 GAN보다는 흐리고 안 좋은 성능을 낸다고 한다.
6.Generative Adversarial Networks (GAN)
지금까지 tractable/intractable 한 density function을 사용하는 generative model들을 살펴보았다. 그런데 만약 우리가 explicit density modeling을 포기하고, 그냥 sampling할 수 있는 능력만 얻을 수 있다면 어떨까? GAN은 이런 아이디어에서 나오게 되었다. 때문에 GAN은 explicit density function을 사용하지 않는다. 대신에 일종의 2인 게임 접근(game-theoretic approach)을 통해 training distribution에서 generation을 하는 방법을 배운다.
이제 구체적으로 어떻게 GAN이 작동하는지 알아보자. 앞서 GAN은 sampling할 수 있는 능력만 원한다고 했다. 그런데 우리가 뽑으려고 하는 분포는 꽤나 복잡해서 직접적인 방법으로 sampling을 하는 것은 어렵다. 일단 간단한 분포를 이용해 sampling을 하고, 비교적 복잡한 분포인 training distribution로의 transformation을 배우는 식으로 이 문제를 해결할 수 있다. 여기서도 마찬가지로 복잡한 분포는 neural network로 나타낸다.
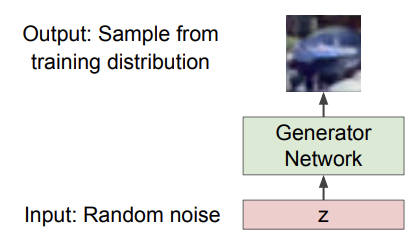
위의 사진과 같은 구조로 sampling이 가능하게 하자는 이야기이다. 이제 어떻게 훈련을 시키는지 알아보자.
1) Training GANs(Two Player Game)
위에서 언급한 2인 게임의 형태로 GAN을 훈련시킨다. 대신에 2명의 사람이 아니라 2개의 network가 게임을 하는 것이다. 여기서 2명의 player이자 2개의 network는 Generator network와 Discriminator network이다.
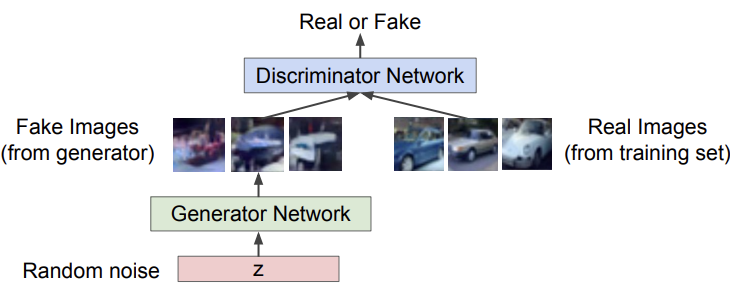
위에서 글로 설명한 GAN은 이러한 구조이다. generator network의 목적은 실제와 같은 fake image들을 만들어 discriminator를 속이는 것이다. 반대로 discriminator network의 목표는 실제와 가짜 사진들 구별을 잘 하는 것이다. 결과적으로 discriminator와 generator network는 fake/real image를 구별하는 게임을 하는 것이다. 좋은 generator network는 실제와 최대한 비슷한 fake image를 만들어 discriminator가 속을 수 있게 하는 network이고, 좋은 discriminator network는 generator에 잘 속지 않고 real/fake image를 잘 구별하는 network이다.
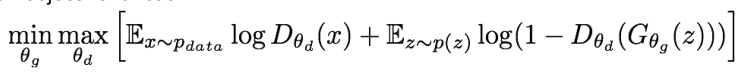
GAN을 훈련할 때는 generator와 discriminator를 하나의 식에서 최소화/최대화 하며 optimization을 진행한다. 이를 강의에서는 minimax objective function이라고 한다. 는 generator의 parameter, 는 discriminator의 parameter를 의미한다. 또, 는 실제 데이터에 대한 discriminator output을, 는 생성된 fake data 에 대한 discriminator output이다. Discriminator는 output이 0과 1사이로 나온다. 1에 가까울수록 실제에 가깝다는 뜻이고, 0에 가까울수록 가짜에 가깝다는 뜻이다. 우리가 원하는 것은 generator는 fake에 가까운 image를 만들고, discriminator는 실제에 가깝게 만들어야 한다. 그렇기 때문에 generator에 대해서는 minimization을 진행해 를 실제(1)에 가깝게 한다. 의 의미가 fake data에 의해 생성된 discriminator output이기 때문에, 이 값이 1에 가깝다면 discriminator가 fake data를 진짜 data라고 생각한다는 뜻이 된다. 즉, generator가 이루려는 목적과 일치하게 되는 것이다. 반면, discriminator에 대해서는 maximization을 진행해 를 실제(1)에 가깝게, 를 가짜(0)에 가깝게 만든다.

최소화와 최대화 문제가 같이 엮여있기 때문에 gradient ascent와 gradient descent를 번갈아 진행한다. 그러나 실전에서는 이렇게 하면 좋은 결과를 얻기 힘들다고 한다. 아래 그래프에서 그 이유를 자세히 알아보자.
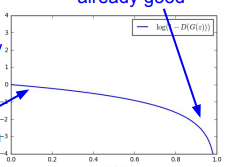
이 generator 그래프의 x축은 을 뜻한다. generator의 성능은 값이 높을수록 좋다. 가 크다는 것은 가 작다는 것이다. 다시 말해 가 작다는 것은, fake data를 discriminator가 fake로 판단한다는 뜻이기 때문에, generator는 이 경우에 많은 것을 배울 수 있다. fake data를 real 하게 판단되도록 해야하기 때문이다. 가 작은 부분의 gradient가 크다면, 학습에 더 좋은 영향을 줄 것이다. 그런데 위의 그래프에서는 부분의 gradient가 작다. 배울 수 있는 것이 별로 없는 것이다. 그래서 gradient descent 대신에 gradient ascent를 도입한다.

gradient ascent를 하기 때문에 를 minimizing하는 것이 아니라 maximizing 하기 때문에 대신 를 사용한다. 그러면 그래프가 가 작을때 gradient가 커지기 때문에, 학습에 더 많은 도움이 된다.
2) GAN Training Algorithm

반복 횟수를 뜻하는 k 값에 따라 최대 성능을 내는 값이 다르다고 한다. 이렇게 훈련이 끝나고 나면, 우리는 generator를 이용해 새로운 이미지들을 만들어 낼 수 있게 된다.

성능이 그닥 좋지는 않다. 그러나 여기에 CNN Architecture를 도입하면 훨씬 좋은 결과를 얻을 수 있다. 그 architecture에 대한 가이드라인은 아래 사진에 있다.

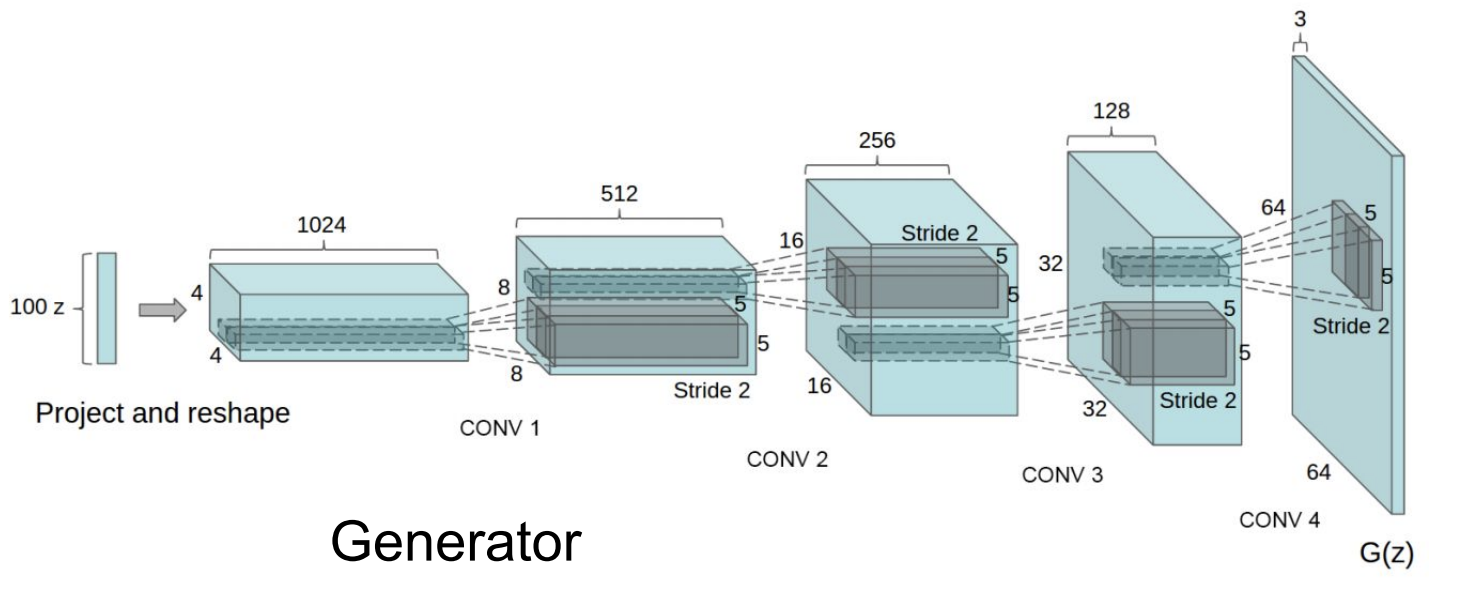
위의 사진처럼 를 input으로 넣어서 최종 를 얻는 것이다. 이렇게 하면 생성된 사진들의 퀄리티가 훨씬 좋아진 것을 볼 수 있다.

3) 는 어떤 역할을 할까?
가 사실 어떤 역할을 하는지 우리가 직관적으로 알 수 없어서, 벡터간의 연산을 통해 의 역할이 무엇인지에 대해 알아보았다.

각 특성을 가진 사진을 3장씩 준비하고, 평균을 낸다. 그리고 세 벡터의 뺄셈/덧셈을 하면, 신기한 결과를 볼 수 있다. 웃는 여자에서 무표정의 여자를 빼고 무표정의 남자를 더하니, 웃는 남자의 사진이 나왔다. 이렇게 z의 역할을 간접적으로라도 확인해볼 수 있다.

