3. Configuration of Neural Networks

1번, 2번 포스트에서는 NN이 무엇이고 어떻게 구성되어 있는지, 학습이란 무엇이고 어떤 방법으로 진행되는지에 대해 간략하게 알아봤다.

그럼 이 NN으로 어떤 것들을 할 수 있냐?
요즘 나오는 인공지능 관련된 서비스들을 모두 할 수 있다. 근데 그 서비스들도 다 분해해보면 크게 Regression/Classification으로 나뉜다.

예시로 chatGPT의 경우도 classification task이다. 사용자가 입력을 주면, 그 다음으로 나올 적합한 단어를 50만개 쯤 되는 단어 뭉치에서 고르는 일을 하는거다.
Regression의 경우는 주로 어떤 값을 예측하는 task를 처리하는데 사용된다.
아주아주 대표적인 예시로는 Boston Housing Dataset을 사용하는 집값 예측 문제가 있겠다.

Classificaion의 경우는 분류 task를 처리할 때 사용한다.
이 사진이 개인지, 고양이인지 구분해줄 때 사용하는거다.

---

1. Regression

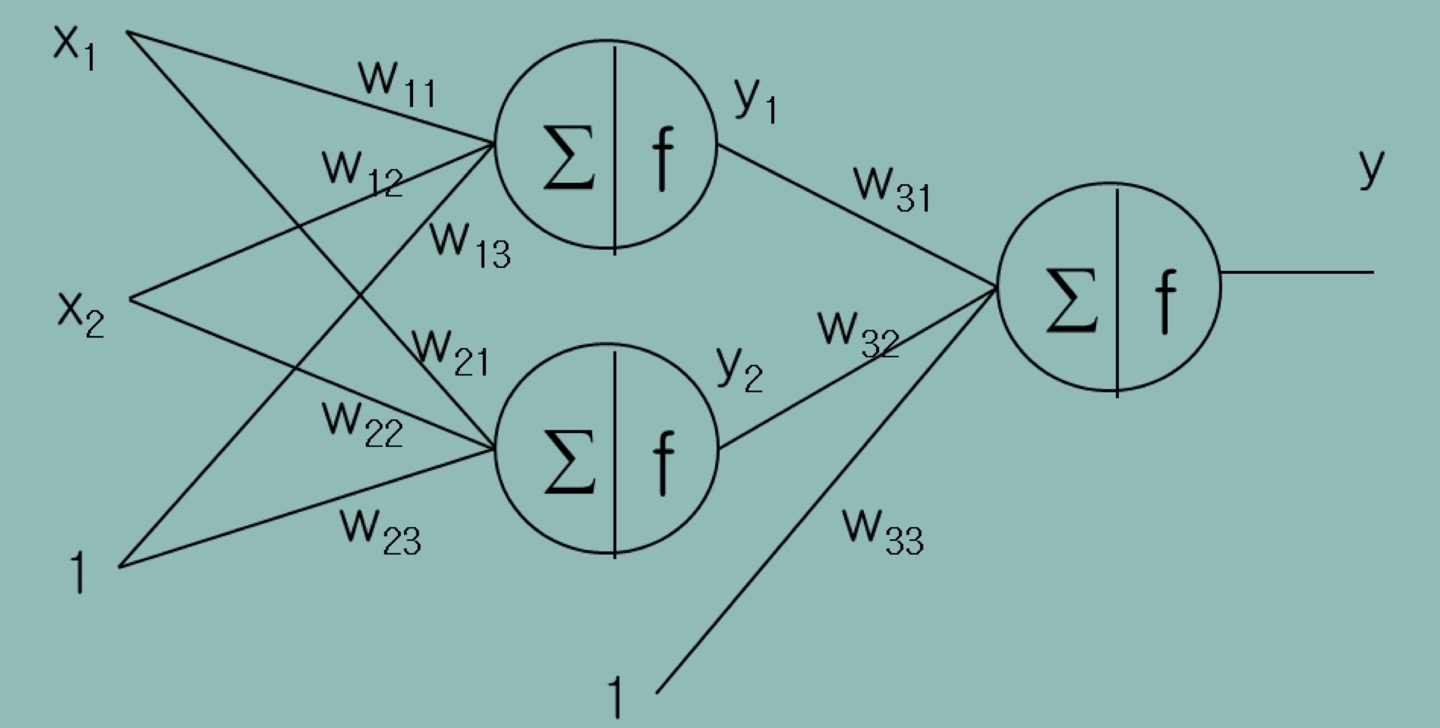
위 사진과 같은 NN이 있다 치자. Activation Function이 ReLU라면, 이 NN은 절대 Regression을 할 수 없을거다. 마지막 노드의 출력이 0 이상으로만 나오니까...
그래서 Regression을 할 때는 마지막 노드의 Activation Function을 Linear하게 설정한다. 말이 어렵지 그냥 y = s를 쓴다는 말이다.

그렇더라도 hidden layer의 activation function은 무조건 non-linear한 함수를 써야한다!
마지막 노드에만 linear function 쓴단 말...

---

2. Classification

2-1. Binary-Class Classification

앞서 Classification의 예시로 개/고양이 인지 구분하는 task를 들었었다. 개/고양이 구분하는 것, 검/빨 구분하는 것들은 output이 2개 뿐이라 Binary-Class Classificaiton이라 하는데, Neural Net의 출력으로 어떻게 구분이 가능할까?

개/고양이, 검은색/빨간색 같이 실수로 표현되지 않는 데이터들을 nomianl value라고 하며, 이 데이터들은 대소관계가 없다는 특징을 지닌다.

이런 nominal value를 real number로 표현하는 문제들은 training data의 label(target)값을 0 또는 1로 주면 해결이 된다.
고양이는 0, 개는 1 이런식으로!
다만, 이제부터 0과 1은 확률로 해석하는 것이 이해하기 더 편하다.

즉, 고양이에 할당된 0은 개일 확률이 0이라는 뜻이고, 개에 할당된 1은 개일 확률이 1이라는 뜻이다.

이렇게 하면 대소관계를 나타내지 않으면서도 실수로 nominal value를 표현할 수 있게된다.

이렇게 바꿔준 데이터로 학습을 시키고, 마지막 output layer 노드의 출력값은 무조건 0과 1사이의 값이 되어야 하므로, activation function은 sigmoid function을 사용한다.

그리고 Loss Function으로 MSE가 아닌 Cross Entropy라는걸 사용하는데...!

2-2. Cross-Entropy

참 생소한 단어다. 엔트로피는 들어봐서 알겠는데, 크로스 엔트로피?

결론부터 말하자면, 이 함수를 Loss function으로 사용하는 이유는, output이 "확률"이기 때문이다.

Output이 확률인거랑 저 함수를 쓰는거랑 무슨 상관인데! 하면 이제 수식을 보면 된다. 매우매우 복잡한 수식이지만, 간략히 설명하겠다

Output이 확률이라 했으니, NN의 목표는 training data가 주어졌을 때, 모든 데이터들을 정확할 확률을 최대화하는 w를 찾는 것이다.
NN의 output을 수식으로 표현하면 다음과 같다.

$\Big(\underset{(x,y)\in Data}{\operatorname{\prod}}NN(x; w)\Big) \times \Big(\underset{(x,y)\in Data}{\operatorname{\prod}}\big(1-NN(x; w)\big)\Big)$

수식의 앞부분이 개일 확률, 뒷부분이 고양이일 확률이라는 것만 알고가면 된다.
결국 이 수식의 값이 최대가 되도록 하는 w를 찾는게 우리 목표가 되겠다.
이걸 또 수식으로 표현하면...!

$\underset{w}{\operatorname{argmax}}\Big(\underset{(x,1)\in Data}{\operatorname{\prod}}NN(x; w) \times \underset{(x,0)\in Data}{\operatorname{\prod}}\big(1-NN(x; w)\big)\Big)$

가 되시겠다. $\underset{w}{\operatorname{argmax}f(w)}$는 f(w)가 최대가 될 때의 w 값을 반환하는 함수다.
이걸 또 계속해서 변환하면 아래와 같다.

$\underset{w}{\operatorname{argmax}}\Big(\underset{(x,1)\in Data}{\operatorname{\prod}}NN(x; w) \times \underset{(x,0)\in Data}{\operatorname{\prod}}\big(1-NN(x; w)\big)\Big)$
$=\underset{w}{\operatorname{argmax}}\log\Big(\underset{(x,1)\in Data}{\operatorname{\prod}}NN(x; w) \times \underset{(x,0)\in Data}{\operatorname{\prod}}\big(1-NN(x; w)\big)\Big)$
$=\underset{w}{\operatorname{argmax}}\Big(\underset{(x,1)\in Data}{\operatorname{\sum}}{\log}NN(x; w) +\underset{(x,0)\in Data}{\operatorname{\sum}}\log\big(1-NN(x; w)\big)\Big)$
$=\underset{w}{\operatorname{argmax}}\Big(\underset{(x,1)\in Data}{\operatorname{\sum}}{y\log}NN(x; w) + (1-y)\log(1-NN(x;w) +\underset{(x,0)\in Data}{\operatorname{\sum}}{y\log}NN(x; w) + (1-y)\log(1-NN(x;w) \Big)$
$=\underset{w}{\operatorname{argmax}}\Big(\underset{(x,y)\in Data}{\operatorname{\sum}}{y\log}NN(x; w) + (1-y)\log(1-NN(x;w)\Big)$
$=\underset{w}{\operatorname{argmin}}\Big(-\underset{(x,y)\in Data}{\operatorname{\sum}}{y\log}NN(x; w) + (1-y)\log(1-NN(x;w)\Big)$

엄청나게 복잡한 수식 변형 과정이 있었는데, 다 필요없고 마지막의 $\underset{w}{\operatorname{argmin}}$ 안쪽의 수식이 Cross Entropy라는 것만 알고 가면 된다. 사실 몰라도 모델 학습하고 이용하는데 전혀 문제가 없다.

2-3. Multi-Class Classification

Binary Class에서는 "확률이 0이다, 확률이 1이다"로 nominal value들을 대소관계 없이 표현이 가능했다.
그런데 Multi-Class의 경우엔 어떨까.
Red, Yellow, Blue를 구분하는 task를 한다고 생각해보자. Binary-Class처럼 한다면 Red = 1.0, Yellow = 0.5, Blue = 0으로 mapping이 될 것인데, 이러면 치명적인 문제가 생긴다.

Red를 Yellow라고 하는 것보다 Red Blue라고 답하는게 더 나쁜 틀림이 되버리는것이다.

이런 현상을 방지하기 위해 사용하는게 One-hot encdoing이다.
Red는 (1, 0, 0), Yellow 는 (0, 1, 0), Blue는 (0, 0, 1)로 표현해주면, 대소관계 없이 각각의 확률값을 나타낸 것으로 해석이 가능해진다.

그럼 이렇게 간단히 끝인가? 거의 그렇다.
왜 "거의"라고 했냐면, 확률이기 때문이다.
확률의 특징은 전부 더했을 때 1이 나온다는 것인데, one-hot encoding만 하고 학습을 시켰을 때, Red가 입력되면 출력으로 (.6, .2, .4) 이렇게 나오는 경우도 생긴다.
사실 이 문제는 activation function으로 sigmoid를 썼기 때문인데,

이걸 해결하기 위해서 Softmax Layer라는걸 쓴다.

Softmax Layer란, 출력 값을 전체 출력값의 합에 대한 비율로 변환해주는 역할을 한다고 이해하면 된다.

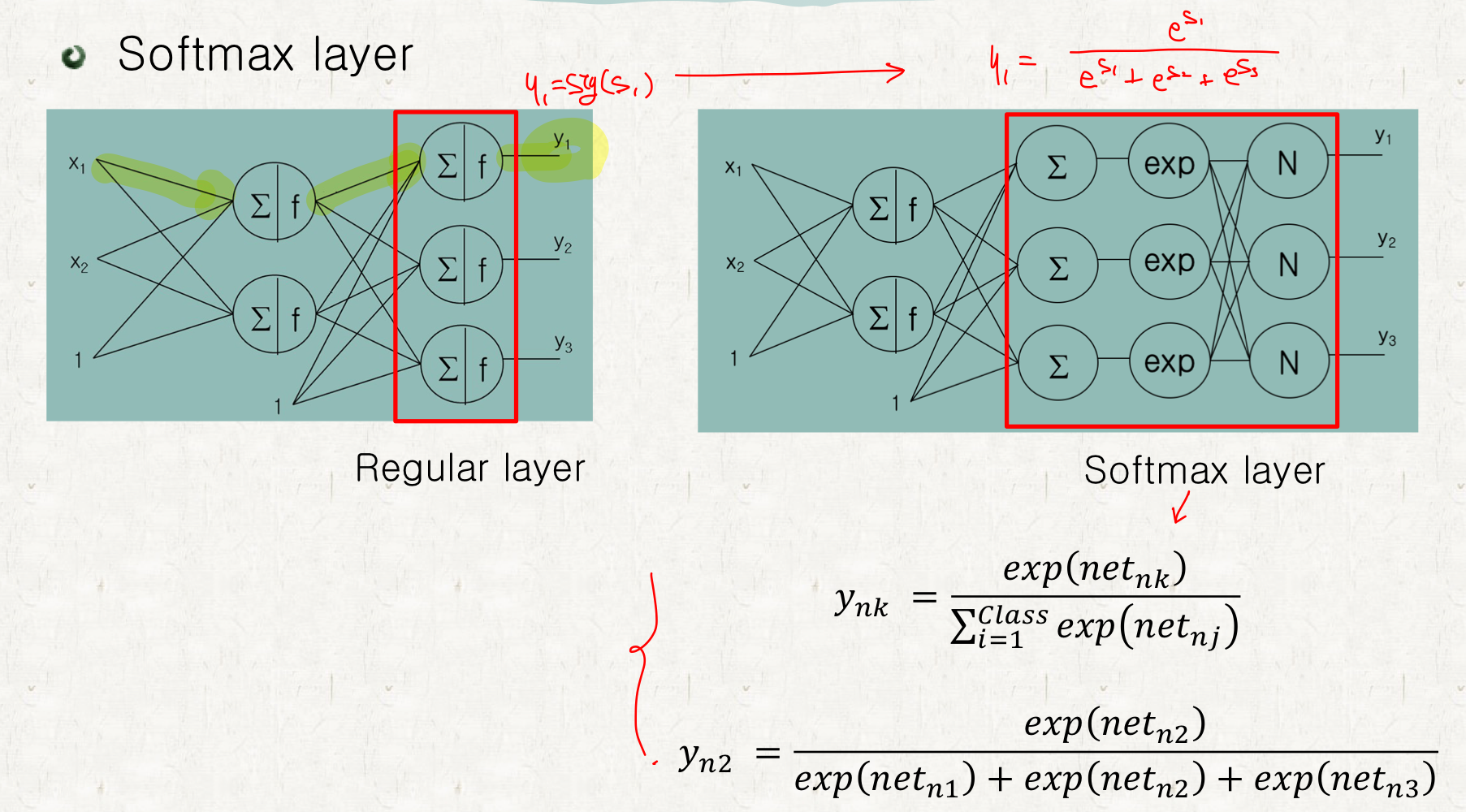
이렇게 변환된다고 이해하면 된다.

마지막으로 Multi-Class Classification의 Error function을 수식으로 표현하면 다음과 같다.

$E = \overset{Data}{\sum_{n=1}}\overset{Class}{\sum_{k=1}}-t_{nk}\log(y_{nk})$

근데 쓰고 보니... 이 수식,    $-\underset{(x,y)\in Data}{\operatorname{\sum}}{y\log}NN(x; w) + (1-y)\log(1-NN(x;w)$과 상당히 유사하다.
그렇다. Binary Class Classification은 사실 Multi-Class Classification의 Special Case였던 거고, 똑같이 Biniary-Class Classification의 output layer도 softmax를 써서 해결이 가능하다.