(작성중)
다층 퍼셉트론
퍼셉트론은 선형 분리가 불가능한 상황에서 일정량의 오류가 생길 수 밖에 없는 한계를 가진다. 이를 극복하기 위해 고안된 것이 다층 퍼셉트론!
- 다층 퍼셉트론의 핵심 아이디어
- 은닉층을 둔다.
은닉층은 원래 특징 공간을 분류하는 데 훨씬 유리한 새로운 특징 공간으로 변환한다.
- 시그모이드 활성함수를 도입한다.
연속값을 가지는 출력을 신뢰도로 간주함으로써 더 융통성 있게 의사결정을 할 수 있다.
- 오류 역전파 알고리즘을 사용한다.
다층 퍼셉트론은 여러 층이 순차적으로 이루어진 요소이므로, 역방향으로 진행하면서 한 번에 한 층씩 그레디언트를 계산하고 가중치를 갱신하는 방식의 오류 역전파 알고리즘을 사용한다.
특징 공간 변환
- 여러 개 퍼셉트론을 사용한 XOR 문제의 해결
- 퍼셉트론 2개를 병렬 결합하면, 원래 공간 를 새로운 특징 공간 로 변환
- 새로운 특징 공간 에서 선형 분리 가능한 문제가 된다.
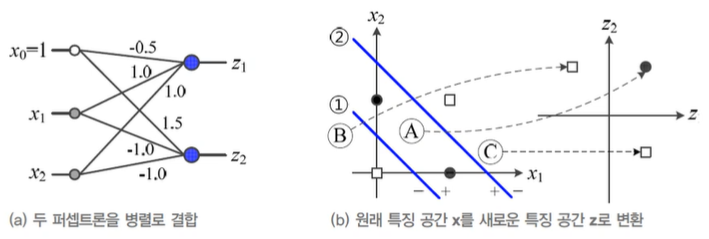
- 추가 퍼셉트론 1개를 순차 결합하면, 해당 다층 퍼셉트론은 XOR 훈련집합의 4개 샘플을 제대로 분류할 수 있게 된다.
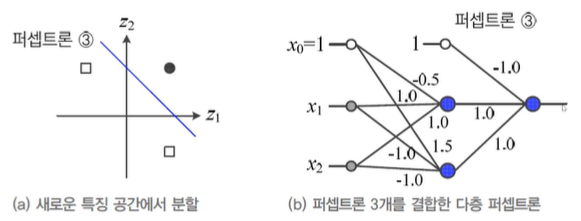
- 다층 퍼셉트론의 용량
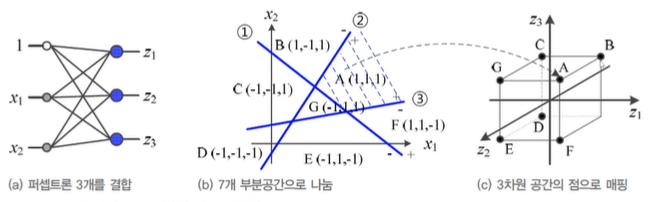
- 일반화하여, p개 퍼셉트론을 결합하면 p차원 공간으로 변환
활성함수
-
활성함수의 공간 분할
- 계단함수는 딱딱한 의사결정: 영역을 점으로 변환
- 그 외 활성함수는 부드러운 의사결정: 영역을 영역으로 변환
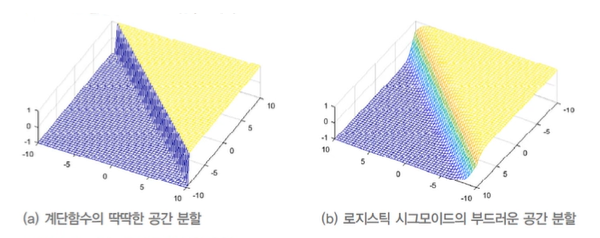
-
시그모이드 활성함수
- 이진 시그모이드 함수: 0 ~ 1의 출력값
- 양극 시그모이드 함수: -1 ~ +1의 출력값 -
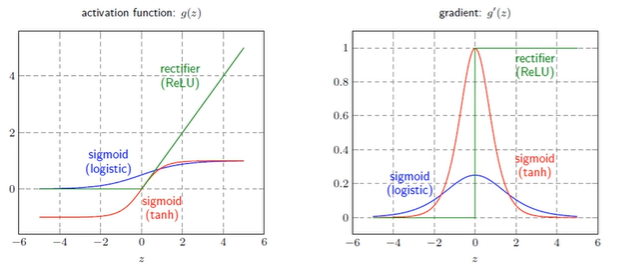
신경망이 사용하는 다양한 활성함수
- 로지스틱 시그모이드(이진)와 하이퍼볼릭 탄젠트(양극)는 값이 커질수록 계단함수에 가까워짐

- 일반적으로 은닉층에서 로지스틱 시그모이드를 활성함수로 많이 사용
- S자 모양의 넓은 포화곡선은 경사도 기반한 학습(오류 역전파)를 어렵게 함(gradient vanishing problem!), 따라서 깊은 신경망에서는 ReLU 활용
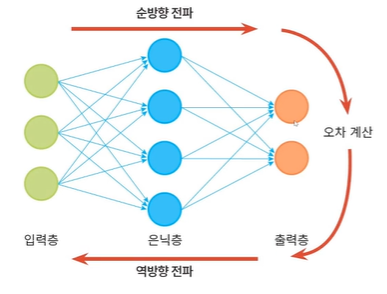
다층 퍼셉트론의 구조
-
입력-은닉층-출력
- d+1개의 입력 노드(d는 특징의 개수)
- c개의 출력 노드(c는 부류 개수)
- p개의 은닉 노드(p는 하이퍼 매개변수, 사용자가 정함)
- p가 너무 크면 과잉적합, 너무 작으면 과소적합(하이퍼파라미터 최적화 필요) -
(2층) 다층 퍼셉트론의 매개변수(가중치)
- 입력-은닉층을 연결하는 (는 입력의 i번째 노드를 은닉층의 j번째 노드와 연결)
- 은닉층-출력을 연결하는 (는 입력의 j번째 노드를 은닉층의 k번째 노드와 연결)

- 입력을 0번째 은닉층, 출력을 마지막 은닉층으로 간주했을 때 일반화하여 는 번째 은닉층의 번째 노드를 번째 은닉층의 번째 노드와 연결하는 가중치
-
다층 퍼셉트론의 동작
- 특징 벡터 x를 출력 벡터 o로 사상하는 함수로 간주

- 노드가 수행하는 연산

- 행렬 표기
-
은닉층 = 특징 추출기!
- 은닉층은 특징 벡터를 분류에 더 유리한 새로운 특징 공간으로 변환
- 현대 기계학습에서는 특징학습이라 부름
- 심층학습은 더 많은 층을 거쳐 계층화 된 특징학습을 함
오류 역전파 알고리즘
출력의 오류를 역방향(왼쪽)으로 전파하여 경사도를 계산하는 알고리즘으로, 반복되는 부분식들의 경사도의 지수적 폭발 혹은 사라짐을 피해야 한다.
- 다층 퍼셉트론의 학습
목적함수의 정의
-
훈련집합
- 특징 벡터 집합(X)과 부류 벡터 집합(Y)
- 부류 벡터는 단발성(one-hot) 코드로 표현됨, 즉 -
기계학습의 목표
- 모든 샘플을 옳게 분류하는 함수 f를 찾는 일!
-
목적함수(손실함수)
- 평균 제곱 오차로 정의
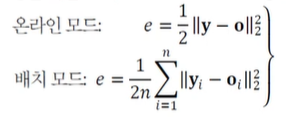
알고리즘의 설계
-
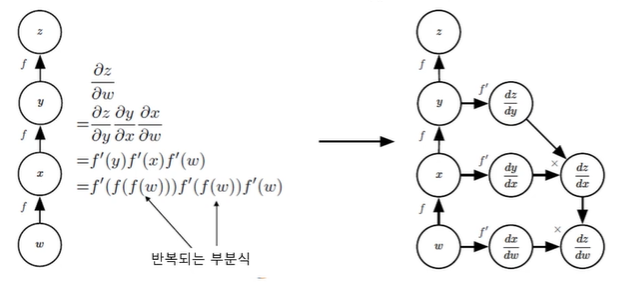
연쇄 법칙(chain rule)의 구현
- 반복되는 부분식들을 저장하거나 재연산을 최소화
-
연쇄 법칙
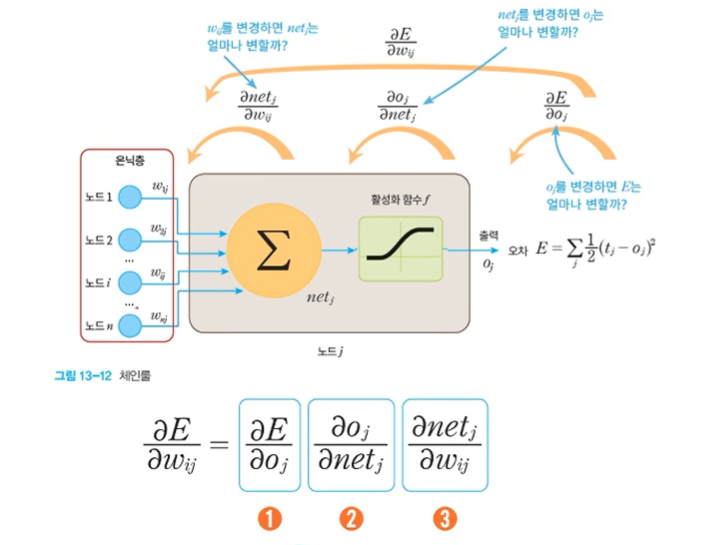
-
역전파 분해
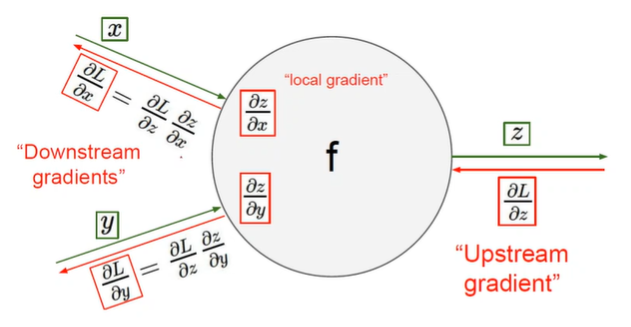
-
단일 노드의 역전파 예
-
곱셈의 역전파 예
-
곱셈의 역전파 Pytorch 구현 예
-
덧셈의 역전파 예
-
S자 모양 활성함수의 역전파 예
-
최대화의 역전파 예
-
전개(fanout)의 역전파 예
모든 경로에 대한 경우들을 다 더하게 됨 -
숫자로 보는 주요 예
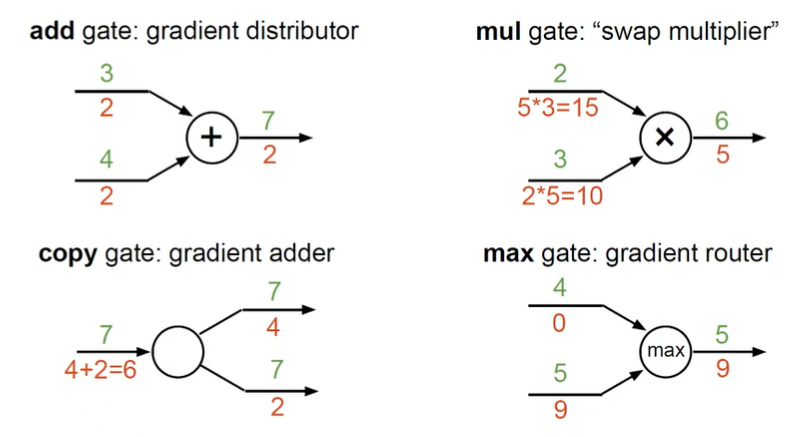
-
실제 역전파 예
-
간단한 전방전파와 오류역전파
학습 알고리즘
-
벡터로 확장한 오류 역전파
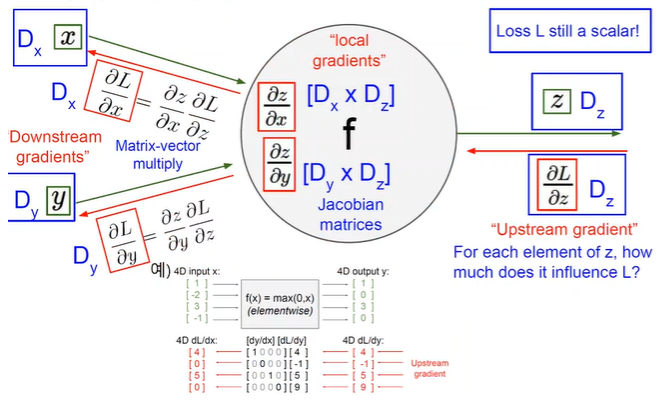
-
행렬 표기 시 GPU를 사용한 고속 연산에 적합하다.
-
미니배치 확률론적 경사 하강법
- 미니배치 방식: 한번에 t개의 샘플을 처리(t는 미니배치 크기)
- t=1이면 확률론적 경사 하강법
- t=n(전체)이면 배치 경사 하강법
- 경사도의 잡음을 줄여주는 효과 때문에 수렴이 빨라지며 GPU를 사용한 병렬처리에 유리
