Deep Neural Networks
Deep Neural Networks(DNN)이란, 은닉층을 깊게(여러층) 쌓은 뉴럴 네트워크를 의미한다.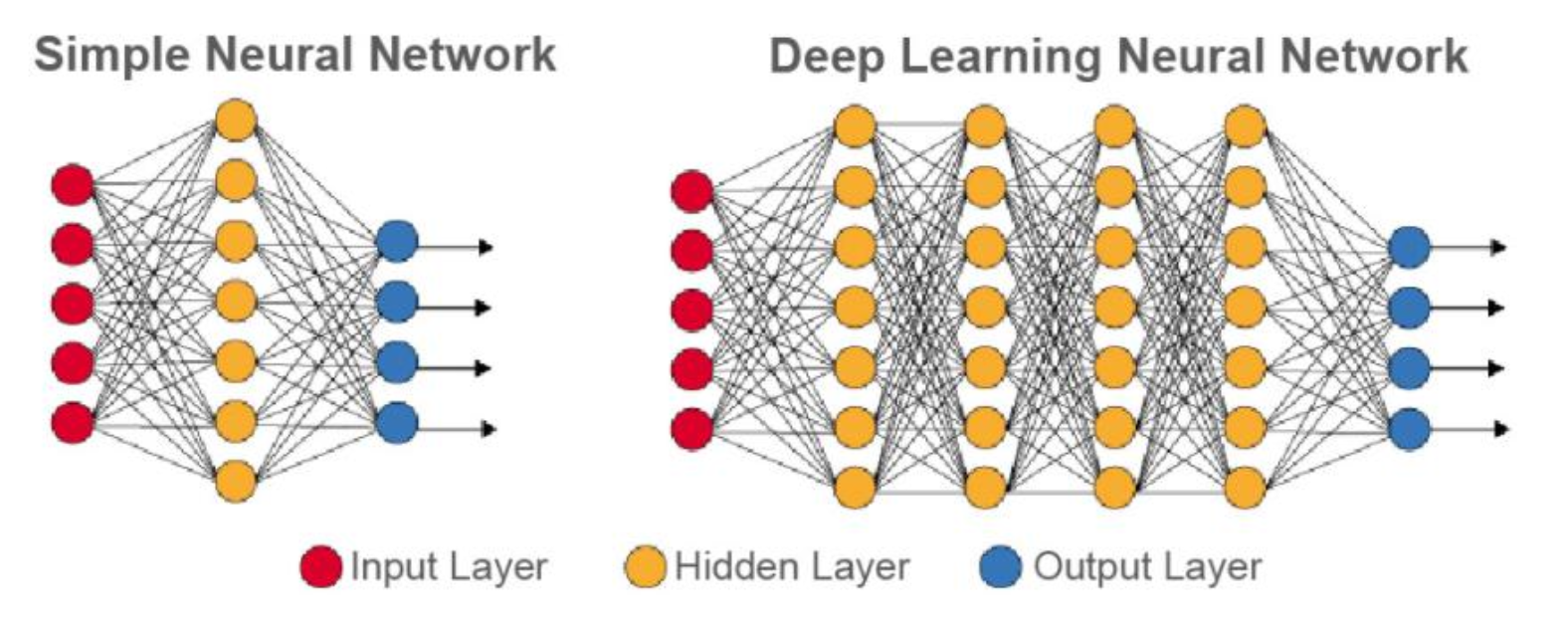
Model Capacity가 증가(More connections)할수록, 계산량이 증가하며 더욱 복잡한 함수를 근사할 수 있게 된다.
충분히 많은 연결(= Many Neurons)이 존재한다면 단 1개의 은닉층만으로도 모든 함수를 근사할 수 있다. 이를 Width가 넓다고 표현한다.
하지만 현실적으로 Depth가 깊은(= Many Hidden Layers) 신경망을 사용하는 것이 일반적이다. 이는 계층적 구조가 여러 이점을 갖기 때문이다.
-
Width가 넓은 신경망보다 간결하다.
-
Width가 넓은 신경망보다 일반화 성능이 좋다.
Width와 Depth가 모두 큰(= Many Neurons and Hidden Layers) 뉴럴 네트워크는 굉장히 복잡한 함수도 근사할 수 있지만, 여러 문제점이 발생한다.
-
과적합(Overfitting) 발생 가능성이 높음
-
최적해를 찾는 속도가 매우 느려질 수 있음
-
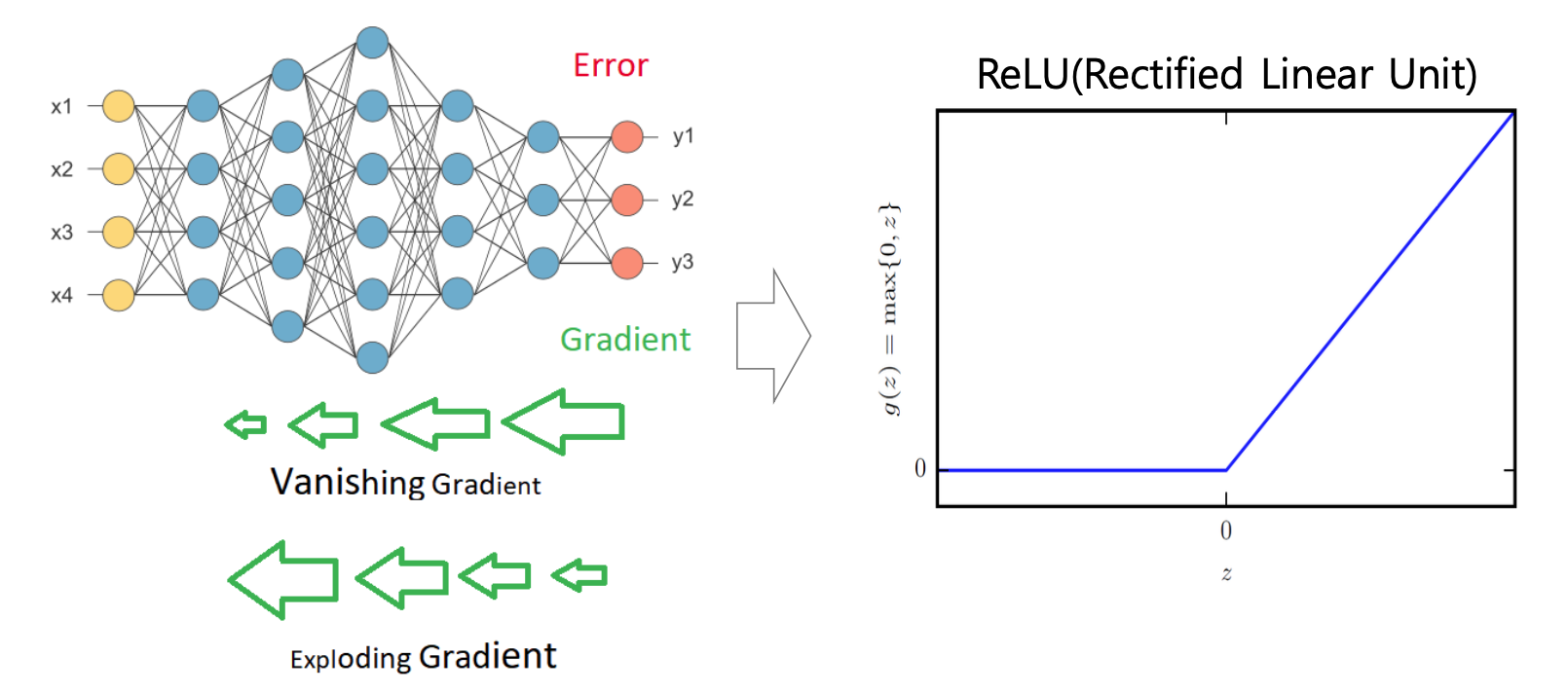
Vanishing/Exploding Gradient(사라지는/폭발하는 기울기)문제가 발생할 수 있음
딥러닝 모델의 본질은 어떤 함수 의 근사(Approximate)하는 것에 있다. 즉, 입력에 대한 정답 함수에 근사하기 위한 과정을 학습이라고 할 수 있다.
-
정답 :
-
근사 :
신경망은 여러 함수들이 연쇄적으로 연결된 구조를 가지며, Depth가 깊을수록 연결되는 함수가 많아진다.
Loss Function
XOR 문제는 비선형 문제 중에도 단순한 편에 속하므로 완벽히 분류가 가능한 반면, 현실 데이터들은 복잡하고 분류가 어렵다.
신경망이 복잡한 데이터를 예측하기 위해선 복잡한 비선형 구조를 가져야 한다. 이로 인해 손실 함수는 복잡한 곡면(Non-convex)를 갖게 된다.
복잡한 손실 함수일수록 많은 Local Optimal(지역 최적해)가 존재하며, 이는 최적화를 어렵게 만든다.
따라서 전역 최적해(Global optimal)에 근사한 지역 최적해를 찾는 것이 현실적인 최적화 목표이다.
또한 초기 가중치를 잘못 설정할 경우, 최적해를 찾지 못할 가능성이 높아진다. 따라서 좋은 초기화 방법을 적용하는 것도 매우 중요하다.
효과적인 Gradient Descent를 위해 Loss function은 다음 조건을 만족해야 한다.
-
연속적이고 미분 가능한 함수
-
기울기가 충분히 커야함
-
기울기가 너무 작은 경우 학습 속도가 매우 느려진다(파라미터 값이 미세하게 업데이트).
-
기울기가 너무 작은 경우 Gradient Vanishing (기울기 소실) 문제가 발생할 확률이 높음
-
-
포화 영역(Saturation, 기울기가 0에 가까워지는 구간)이 없어야 함.
Hidden Layer
입력층이나 출력층은 어떤 신호들이 사용되며, 어떤 파라미터를 갖는지 비교적 직관적이다.
반면 은닉층의 파라미터들은 모델 내부적에 존재하는 학습 대상이기 때문에 직관적이지 않고 내부적으로 어떻게 동작하는지 불분명(Black box)하다.
즉, 은닉층은 Implicit하게 동작하기 때문에 명확히 해석하기 어렵다는 특징이 있다.
은닉층에 적용할 활성화 함수 중 어떤 활성화 함수가 최고의 선택이 될지 예측하는 것은 매우 어렵다. 따라서 은닉층의 활성화 함수는 여러번의 시행과 검증(Validation)을 거쳐 결정하는 것이 올바르다.
-
ReLU
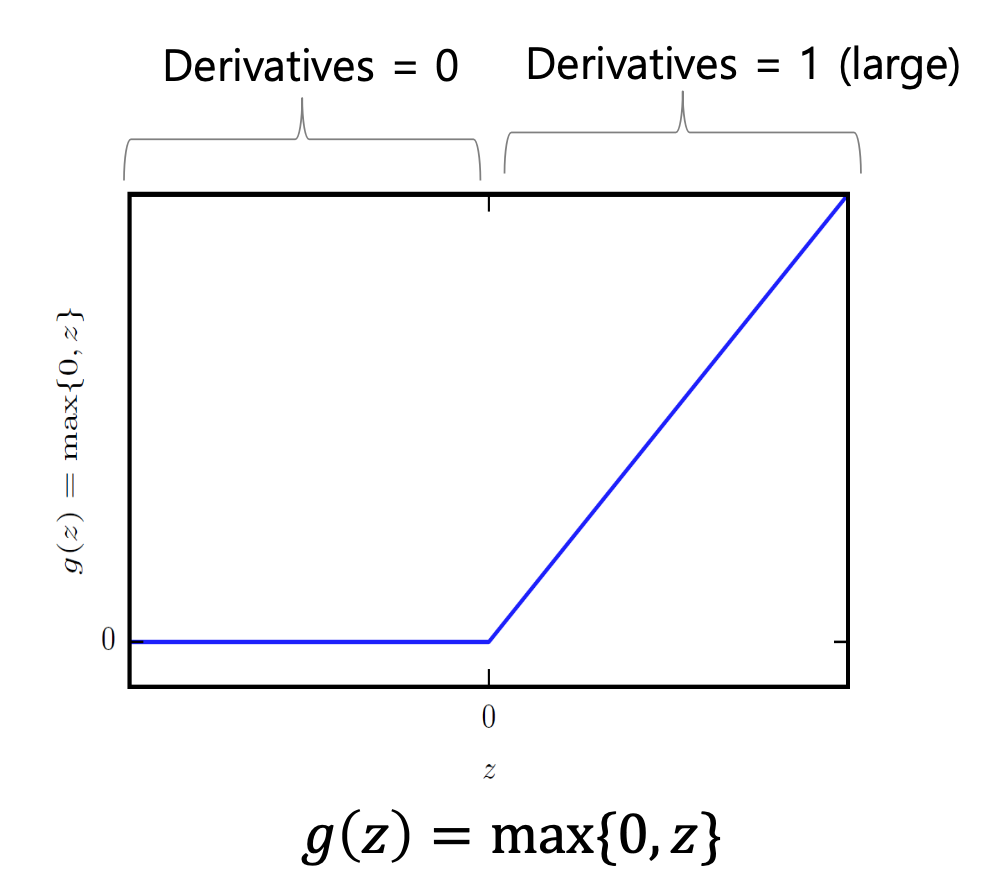
-
계산이 단순하며 빠르다
-
양의 구간에서 기울기가 1로 일정
-
일정값 미만에서 활성화 값이 0이 되어 해당 뉴런이 비활성화되는 경우 존재
-
이러한 문제점을 해결하기 위해 여러 ReLU의 변형 함수들이 존재
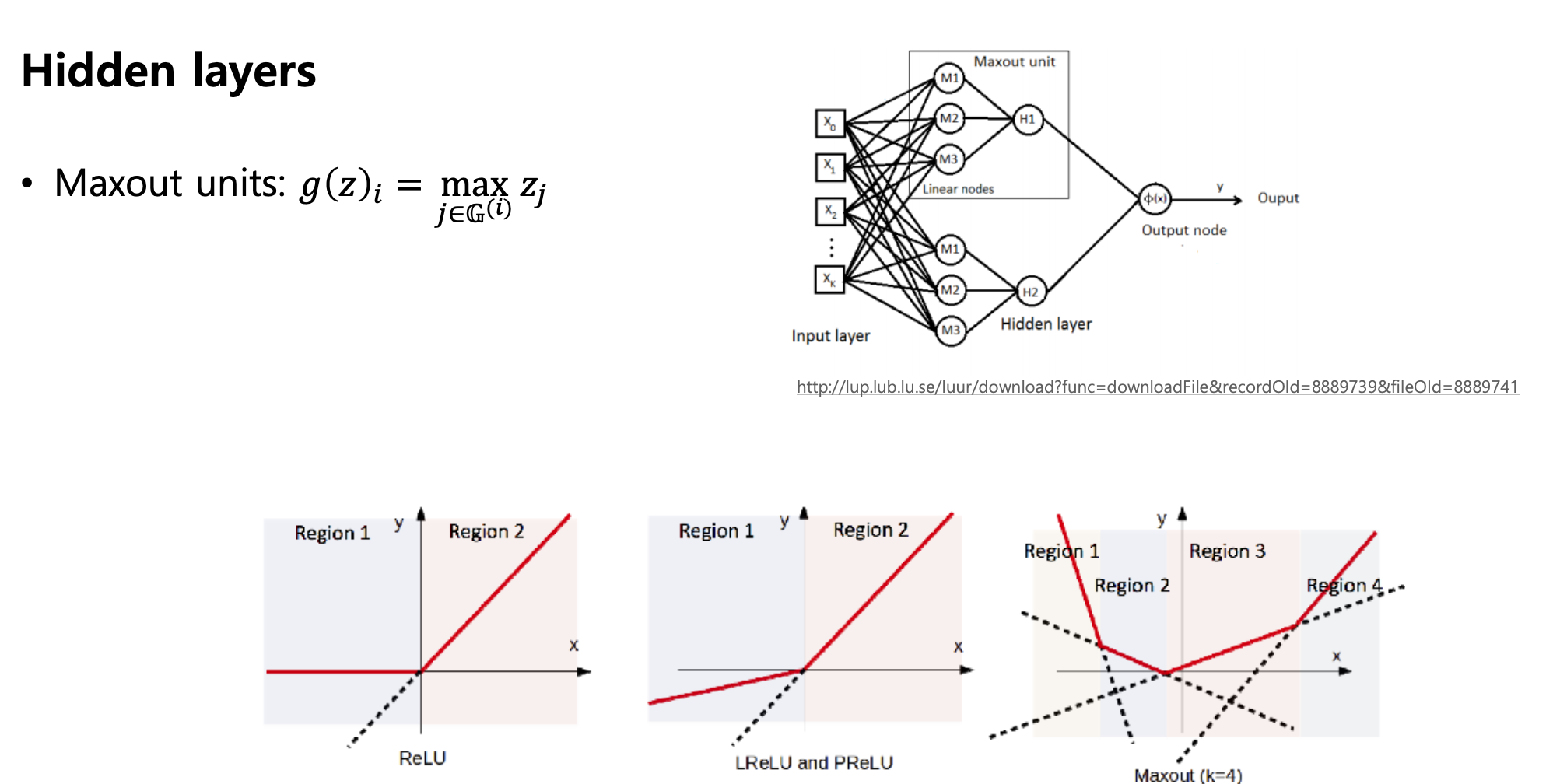
-
-
Logstic Sigmoid and Hyperbolic Tangent
-
두 함수는 0에서 멀어질수록 포화(Saturate)상태가 된다. 이는 입력 신호가 0에서 멀어질수록 민감도가 떨어진다는 것을 의미한다.
-
두 함수는 DNN과 같은 네트워크에서 사라지는 기울기와 같은 문제가 발생할 가능성이 높아 잘 사용되지 않는다.
-
두 함수는 주로 Recurrent Networks와 같은 환경에서 사용된다.
-
