[CS231N] Lecture 4 | Introduction to Neural Networks

CS231N - Lecture 4 | Introduction to Neural Networks

Backpropagation

역전파 알고리즘은 출력값에 대한 입력값의 기울기(미분값)을 출력층 layer에서부터 계산하여 거꾸로 전파시키는 것이다.

이렇게 거꾸로 전파시켜서 최종적으로 출력층에서의 output값에 대한 입력층에서의 input data의 기울기 값을 구할 수 있다.

이 과정에는 중요한 개념인 chain rule이 이용된다.

출력층 바로 전 layer에서부터 기울기(미분값)을 계산하고 이를 점점 거꾸로 전파시키면서 전 layer들에서의 기울기와 서로 곱하는 형식으로 나아가면 최종적으로 출력층의 output에 대한 입력층에서의 input의 기울기(미분값)을 구할 수가 있다.

Backpropagation은 가중치를 계산하는 방식으로 생각하고,
Gradient Descent는 가중치를 업데이트하는 방식이라고 생각하면 된다.

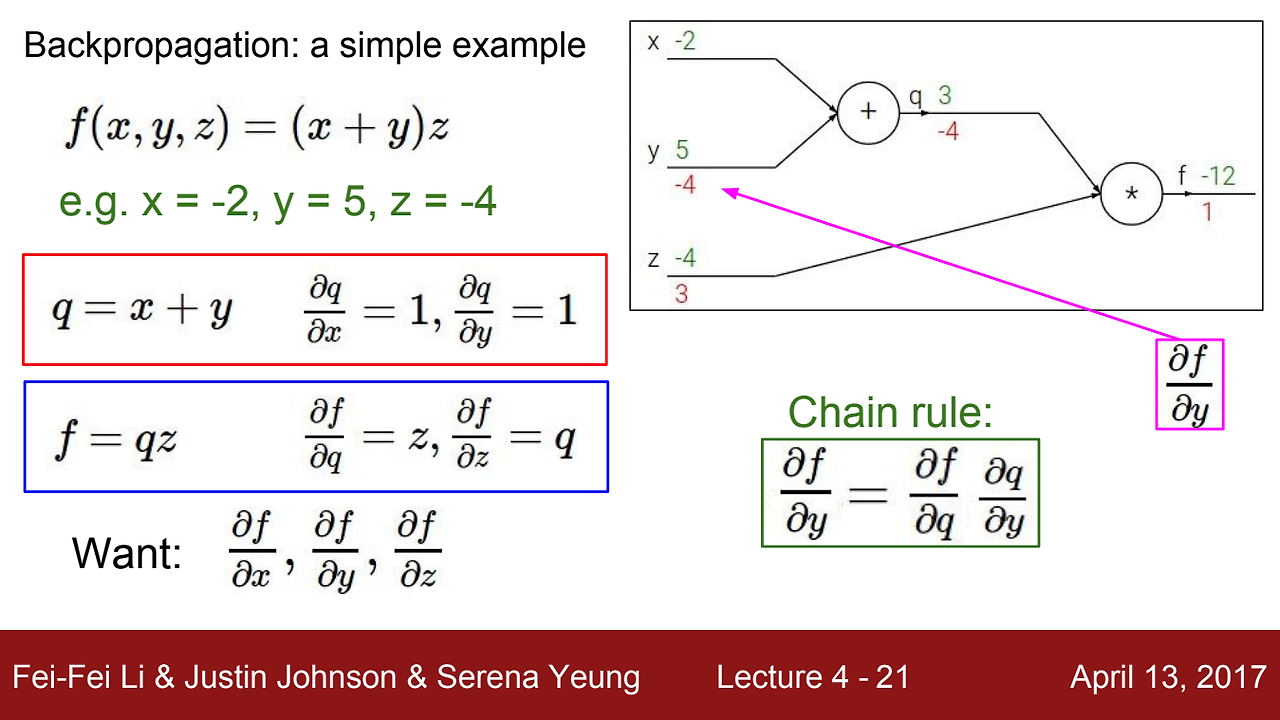
우리가 알고자 하는 것은 x가 f에 미치는 영향, y가 f에 미치는 영향, z가 f에 미치는 영향이다.

• $\frac{df}{dx} =$ x가 f에 미치는 영향
• $\frac{df}{dy} =$ y가 f에 미치는 영향
• $\frac{df}{dz} =$ z가 f에 미치는 영향

덧셈 연산에서 미분은 1이고, 곱셈 연산에서는 서로의 값을 가지게 된다.
EX) $y = qz$ 이면, $\frac{dy}{dq} = z$ 이다.

이제 최종 $f$값부터 반대로 거슬러 올라가며 가중치를 계산해주면 그림과 같은 값들을 얻게 된다.

앞서 말했던 영향력에 대해서 설명하면, $y$가 $h$만큼 증가하면 $f$는 $4h$만큼 감소한다. 이때 $q$는 같은 그라디언트를 갖고 있기 떄문에 똑같이 $h$만큼 증가한다.

Chain Rule (연쇄 법칙)

: 합성 함수에 대한 미분 법칙

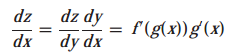
$f$가 실함수(real-valued function)이고, $z=f(y)$이며 $y$는 $x$의 함수이고 $y=g(x)$라고 하면 $z$는 대입에 의해 $x$의 합수가 된다. 즉, $z=f(g(x))$이며, 다음과 같은 연쇄 법칙을 갖는다.

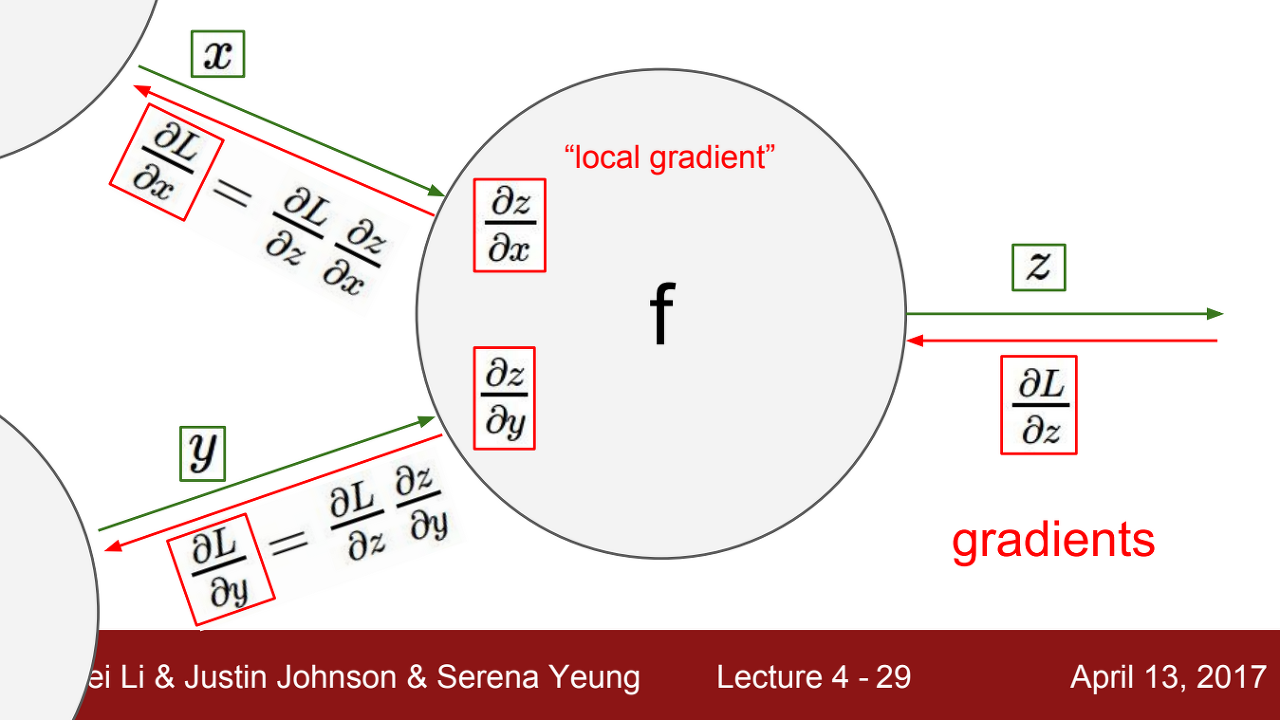
• Forward pass 시에 local gradient를 구한다.
• Backward pass 시에 global gradient를 구한다.
  $\rightarrow$ local gradient * global gradient 를 곱해서 gradient를 구하게 된다.

시그모이드 함수가 예시로 나왔는데, 앞서 했듯이 아래의 식을 참조하여 그라디언트를 구하면 위의 그림과 같이 나온다. 하지만, 하나하나 chain rule을 이용하여 구한 그라디언트는 아래 그림과 같이 sigmoid gate로 한번에 계산이 가능한다.

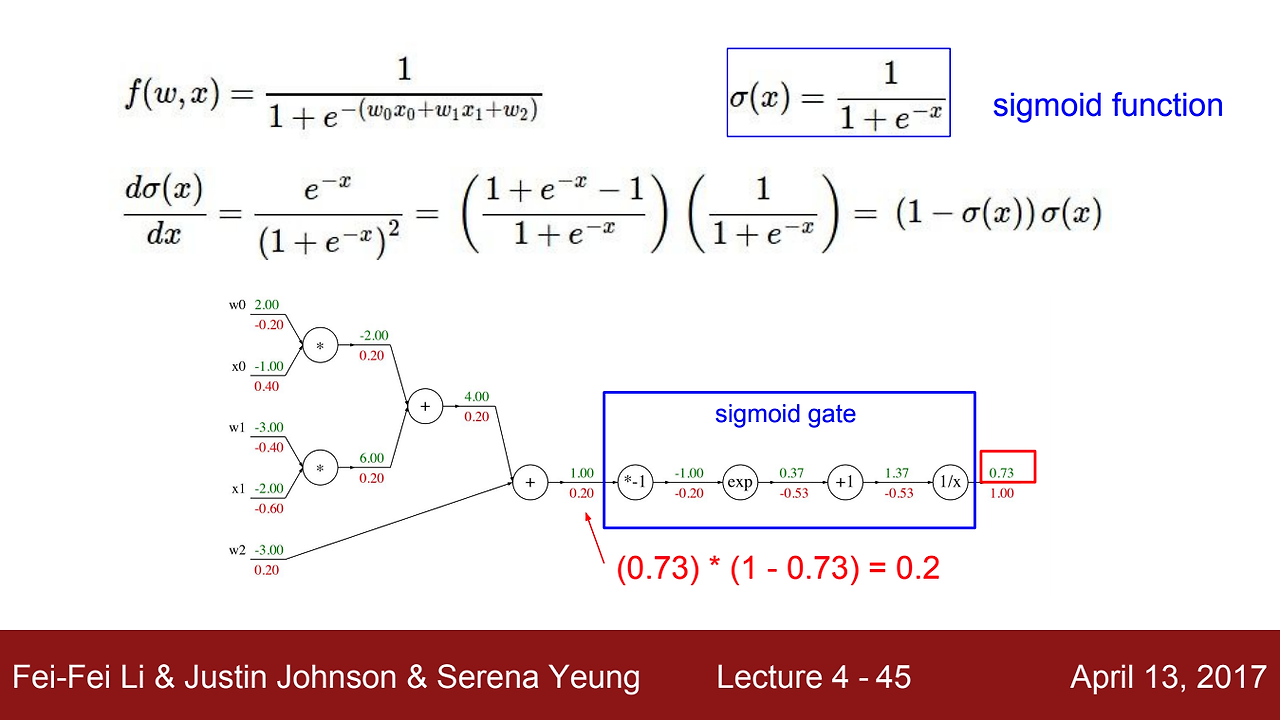
이것이 sigmoid 함수의 장점이다 !

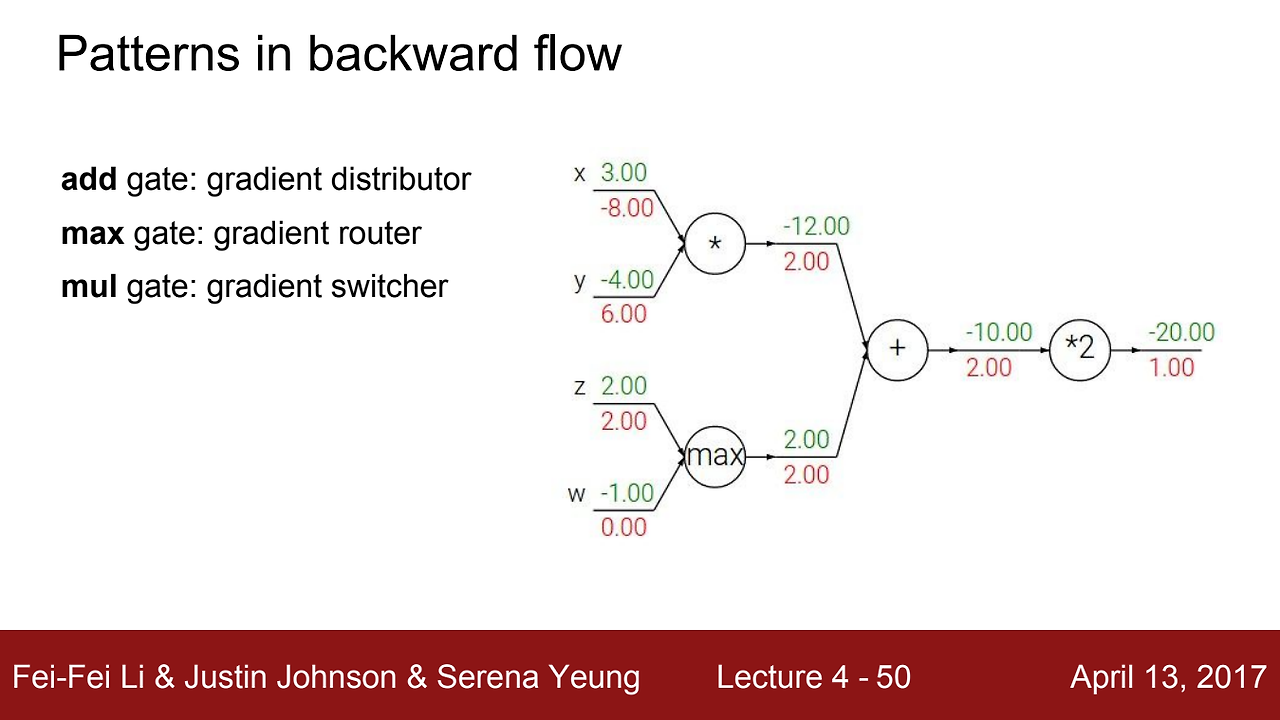
우리는 각 게이트를 일반화시킬 수 있다.

• add gate : gradient distributor (그라디언트를 동일한 값으로 전파해주는 역할)
• max gate : gradient router (더 큰 값에 값을 부여해주는 역할)
• mul gate : gradient switcher (서로의 값을 바꿔주는 역할)