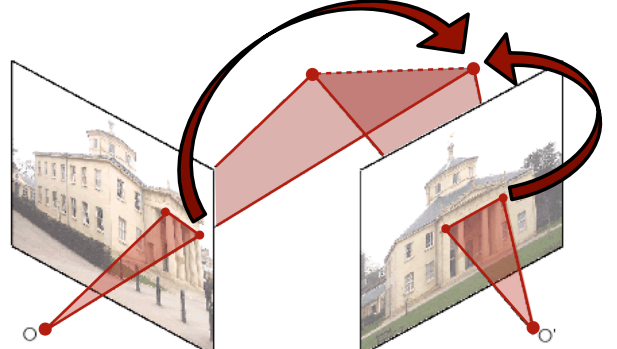
Example: Image Alignment Using Corresponding Points

다음 사진과 같이 같은 배경을 찍은 서로 다른 두 사진이 있을 때 각각의 일치하는 부분을 매칭하는 과정을 설명하고 있다.

Image Alignment
: 같은 scene을 찍고 있지만, 다른 condition에서 찍은 사진들을 겹치는 과정

일치하는 부분을 매칭시키면 두 사진을 다음과 같이 overlaying할 수 있다.

---

Estimating 3D Information

해당되는 지점 + 카메라의 위치를 고려하면 3D로 해당 위치를 계산할 수 있을 것이다.

이 과정을 통하여 2D사진 여러개로 3D를 구현할 수 있는 것이겠지.......?

---

Data Association

알 수 있는 사실

• 만약 우리가 corresponding points를 알고 있다면, (+카메라의 위치까지)
  ⇒ 3D reconstruction을 이루어낼 수 있다. 위의 사진처럼
• stereo image matching에서 사진들은 비슷한 condition에서 찍혀져야 한다.
  => 당연하지! matching해야 되는데 아예 겹치는 것이 없다면 말이 안되니까

Can we localize a local image patch in another image?
이제 여기서 의문이 생기지.
그러면 도대체 어떻게 matching을 하는 것인가?
한 사진을 다른 이미지에서 어떻게 위치를 찾을 수 있는 것인가?

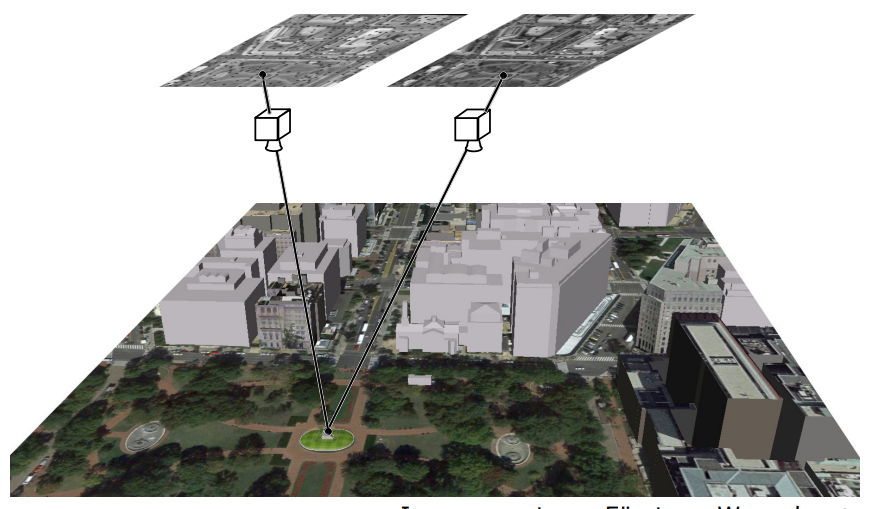
위의 사진과 같이 헬기를 타고 같은 scene을 다른 condition에서 찍은 두 장의 사진을 보자.
두 사진이 찍힌 시간 사이에는 몇초 또는 몇분이 있을 것이다.

• 두 사진의 색이 다른 이유?
  : 사진 찍을 때 카메라 빛 흡수의 차이 같은게 이유가 될 수 있겠지

뒤에서 말하는 cross correlation을 이용하면 두 이미지가 correspond하는 부분을 찾을 수 있다!

---

Template Matching

Template Matching
: larger image 안에서 small template image의 위치를 찾는 것
: 일반적으로 size of template << size of image

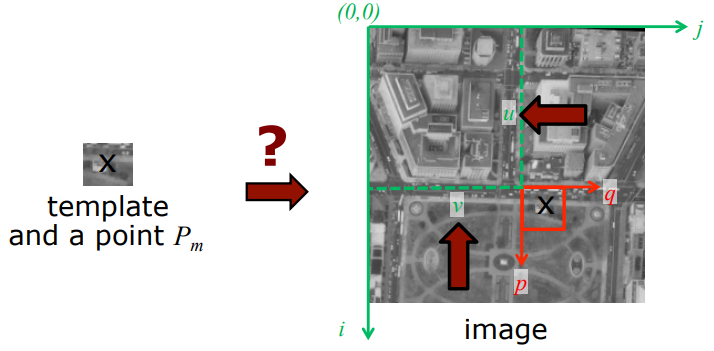
위치는 어떻게 표현할까?
다음과 같이
큰 image의 좌표축 i,j와
template의 좌표축 p,q를 이용하여 나타낸다.

이때, u와 v는 두 좌표축의 위치가 얼마나 떨어져 있는지 알려주겠지.

u와 v의 값을 아는 것이 중요하고 이는 offset이라고 부름

다시 한번 간단하게 정리하면,

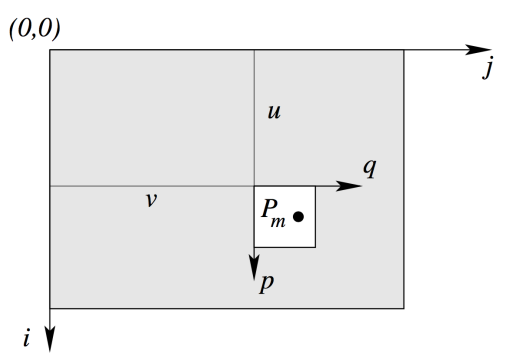
imag $g_1(i,j)$ 와 template $g_2(p,q)$ 가 주어지고, $g_1$과 $g_2$ 사이의 offset인 $[\hat{u},\hat{v}]$을 찾기 !

Assumptions

Geometric transformation

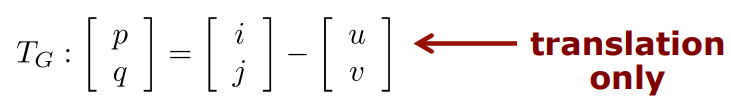
• 2개의 unknown은 $p_G = [u,v]^T$
  (변수가 2개라고 생각)

Radiometric transformation

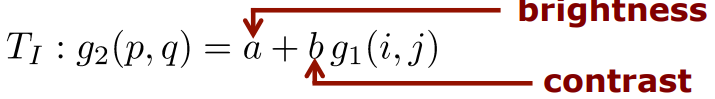
• $g_2$에 있는 모든 각각의 픽셀의 intensity는 $g_1$에 있는 픽셀과 선형독립이다.
• 2개의 추가적인 unknown은 $p_R = [a,b]^T$이다.

pixel intensity
: 특정 픽셀의 밝은 정도를 의미함
:예를 들어, grayscale에서 흰색이면 intensity가 255이고 검은색이면 intensity가 0이다.

Problem definition

이때, 원래 unknown들은 $u,v,a,b$로 총 4개지만,
우리는 일단 $a,b$는 고정하고 $u,v$만 생각하는 것으로

우리의 목표:
해당하는 intensity value의 값의 similarity가 최대가 되게 하는 $[\hat{u},\hat{v}]$ 을 찾는 것 !

이제 질문이 생기겠지
그러면 similarity를 어떻게 측정하는가 ..........?

---

Typical Measure of Similarity

기존이 similarity 측정 방법들
다음과 같은 방법을 이용했을 때는 값이 작을수록 더 similar하다라고 얘기할 수 있겠지!

그러나 문제 발생,
다음과 같은 식은 brightness와 contrast에 의해 영향을 받기 때문에 (radiometric transformation) 적합한 방법이 될 수 없다 !

그래서 제시되는 것이 뒤에 나오는 cross correlation 방법 !

---

NCC(Normalized Cross Correlation)

SSD나 SAD같은 기존 측정 방법들의 문제점을 해결한 것이니까
당연히 CC는 brightness와 contrast에 강한 장점이 있다.

가장 좋은 offset의 값인 $[\hat{u},\hat{v}]$은
가능한 모든 location을 조사해봤을 때
cross correlation coefficient가 가장 큰 경우일 것이다.

그렇다면 왜 brightness와 contrast의 영향을 받지 않을까?
: 각각의 variation을 사용하여 CC를 구하고 있으므로
brightness와 contrast가 발생하여 mean이 증가하더라도
모든 pixel의 값이 동일한 값으로 증가감소하기 때문에
variation은 그대로기 때문이다!

왜 $g_1(u,v)$라고 표현할까?
: 우리는 전체의 image에 대한 분산이 궁금한 것이 아니라
template과 겹치는 부분의 분산이 궁금한 것이기 때문이다 !

그렇다면 $g_2는 ?$
: $g_2$의 크기는 template의 크기와 같은 것이니까 따로 변수가 필요없지

$\sigma_{g_2}$ 구하기

M : template 안에 있는 픽셀의 개수
그림으로 간단히 표현하면 다음과 같은 상황

$\sigma_{g_1}(u,v)$ 구하기

$\sigma_{g_2}$ 구할 때랑 완벽하게 동일한 방법이지

$\sigma_{g_1g_2}(u,v)$ 구하기

공분산 개념과 동일하기 때문에 어렵지 않다. 값이 크면 클수록 비슷한 것이고 작으면 작을수록 다른 것이겠지

---

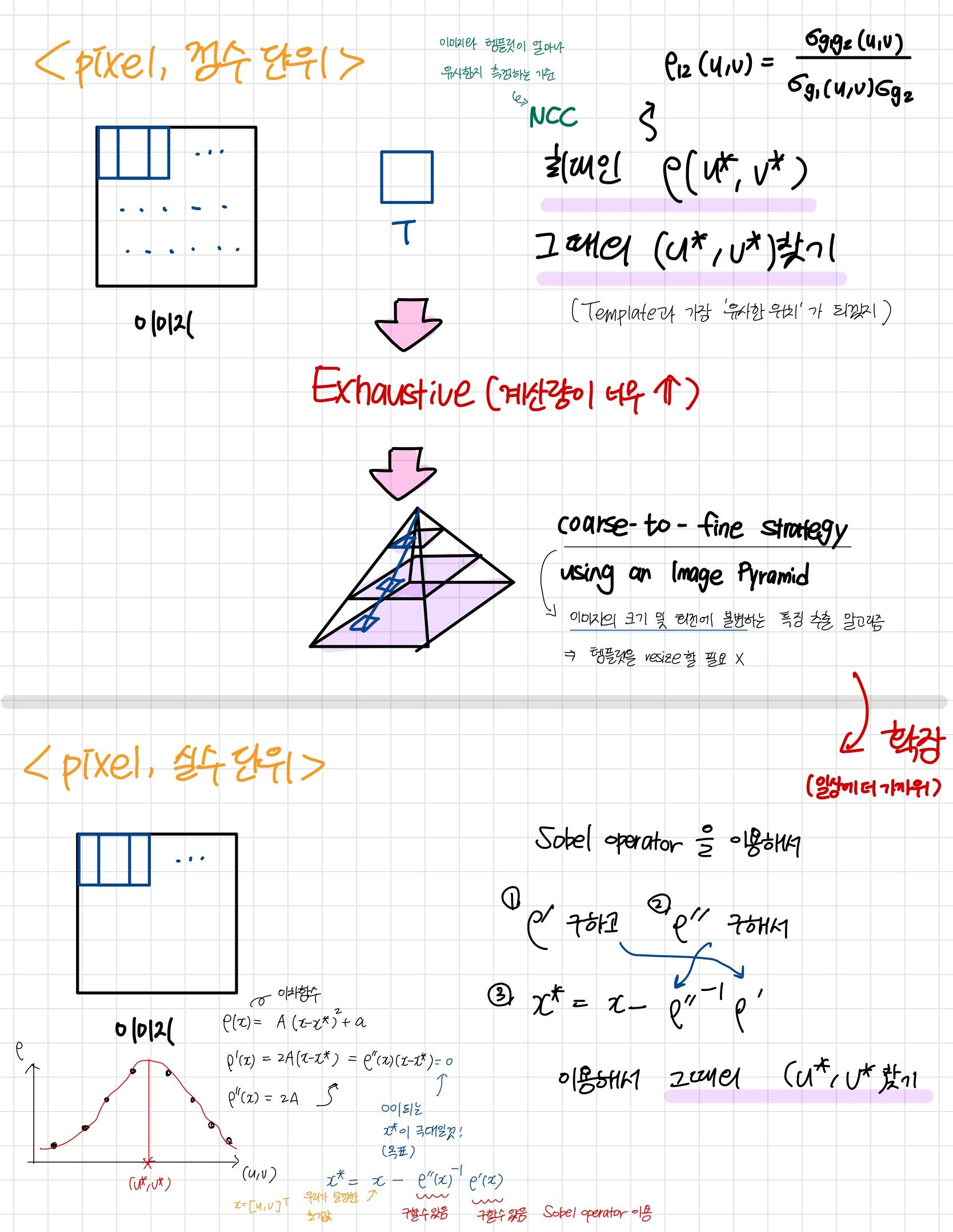
Exhaustive Search

NCC 좋은 방법이긴 한데 ... 꽤나 구해야될게 많아서 힘든 작업이다.

어떤 방법으로 best estimate인 $[u,v]$를 구할 수 있을까?

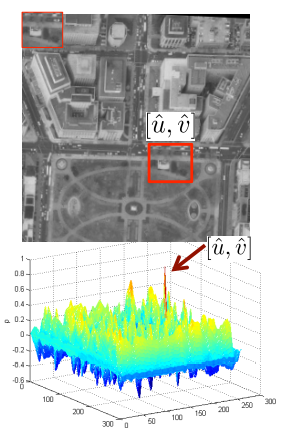
(STEP1) 모든 offset $[u,v]$에 대하여 $\rho(u,v)$를 구하기
(STEP2 $\rho(u,v)$가 최대가 되는 offset $[u,v]$을 찾아내기

Exhaustive Search의 문제점

• 이론상으로는 rotation과 다른 parameter에 대해서도 찾을 수 있지만, exhausitive search 방법으로는 계산량이 너무 많아져 미친듯이 복잡해짐
• Complexitiy가 기하급수적으로 증가함, search space의 차원이 커질 때마다...
  

---

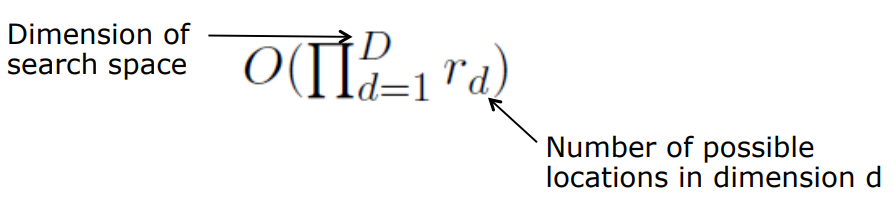
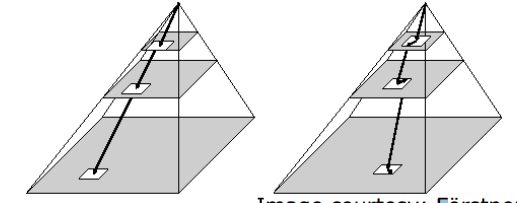
Coarse-To-Fine Strategy Using an Image Pyramid

모든 픽셀에 대하여 작업할 경우 너무 exhaustive하므로 제안된 방법이다.

original image의 모든 location을 돌면서 값을 구할경우 complexity가 너무 증가하기 때문에 downscaled size에서 시작하여 original size로 가는 방법을 이용

---

NCC Example

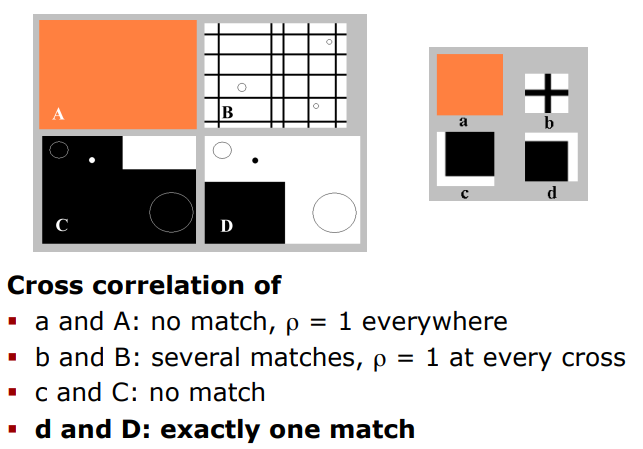
A,B,C,D : image a,b,c,d : template

• a and A : 모든 곳에서 $\rho$의 값이 1로 같으니 no match (예를 들어, offset [2,2]이 [10,10]보다 NCC가 더 크다는 이런 얘기 못하잖아)
• b and B : 교차점이 생길 때마다 match가 되니까 x unique, o several
• c and C : NCC값이 가장 큰 offset을 찾을 수 있을테지만, 유사도가 떨어져 상관계수 값이 그렇게 크지 않으니 우리가 고려할 필요 없음
  ($\rho$=-1이면 match하지만, 우리는 $\rho$가 0.8이상인 곳만 생각 중임)
• d and D : 오직 하나의 match만 발생

---

Subpixel Estimation for CC

Subpixel이 제안된 배경?

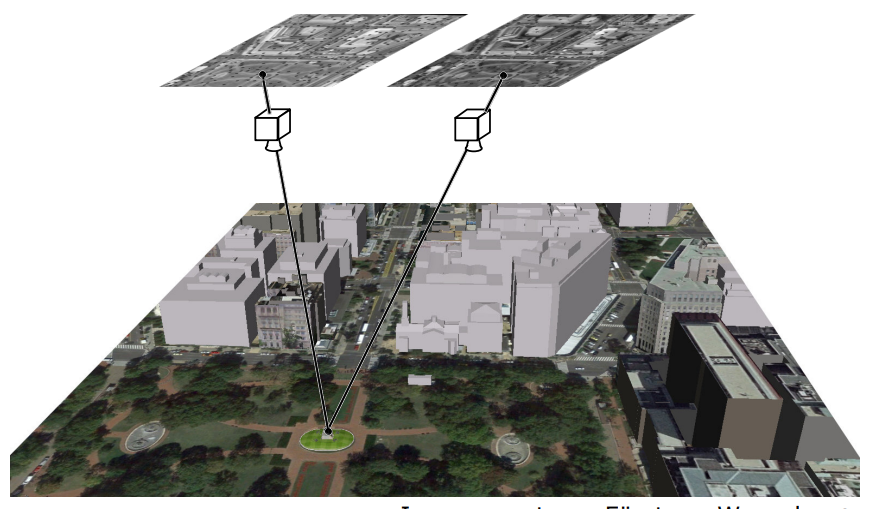비행기에서 사진을 찍다보면 정확히 한 pixel 이동해서 다음 사진을 찍는 것은 거의 불가능하고 1.8pixel 또는 2.9pixel 등 소수점 단위가 나올 것이다.
⇒ 이런 경우를 다루기 위해 제안되었음 (정수가 아닌 소수점까지!)

• CC를 이용한 template matching의 결과는 정수
• 더 정확한 estimate값은 subpixel estimation을 통해 얻어질 수 있음
  

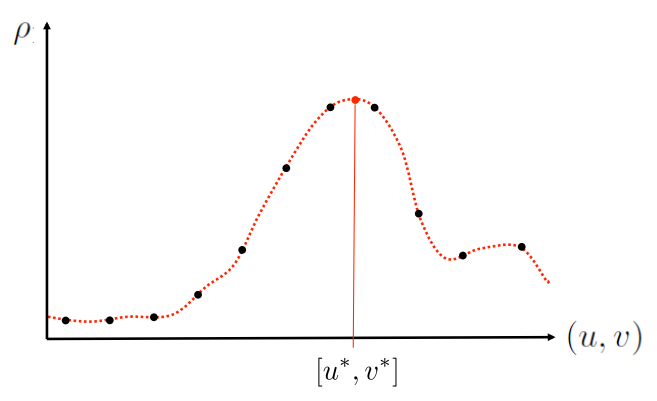
1. 우리가 integer값들로 얻게 된 검정색 점
2. 이들을 연결한 continuous한 함수를 예측
3. 이 함수의 함숫값들 중 가장 큰 NCC값을 갖는 그때의 u와 v (optimal solution)를 구함

Procedure

1. 초기위치 $[\hat{u},\hat{v}]$ 주변에서 $\rho_{12}(u,v)$값을 통하여 locally smooth surface 찾기

• 초기위치는 아마 NCC값이 높은 곳이 기준이 되겠지?

2. local maximum 찾기

(1) Fit a quadratic function around $[\hat{u},\hat{v}]$ (초기값 주위에서 2차함수 찾기)

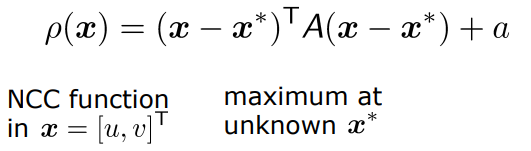
(2) Compute first derivative (1차 미분값 구하기)

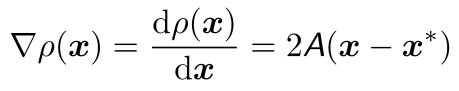
(3) At maximum

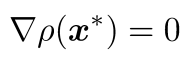
전혀 어렵지 않은 과정이지.
당연히 NCC과정에서 최적의 estimate값을 시작점으로 두고
그 주변에서 2차 함수를 찾고
1차 미분값 = 기울기가 0인 곳이 바로 극대가 될 것이니

---

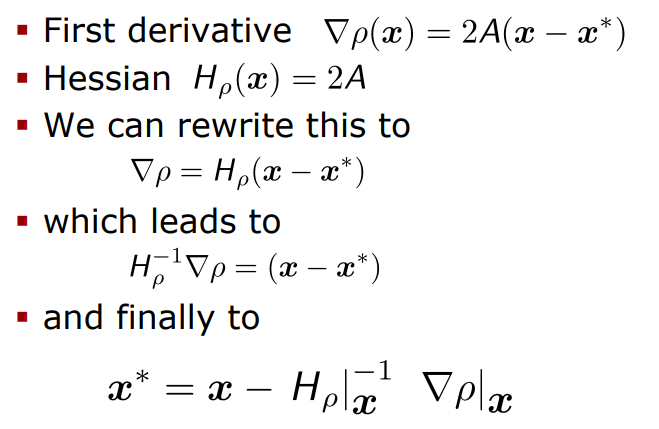
Discussion

• CC는 오직 translation만 고려했을 때 optimal solution을 제공
• subpixel estimation을 사용하면, 우리는 1/10 pixel precision을 얻을 수 있음
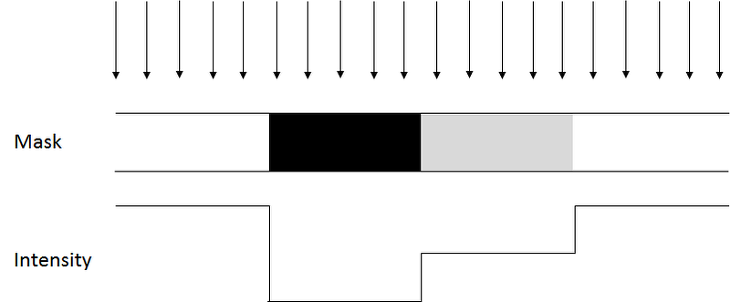
• CC는 occlusion은 다룰 수 없음
  - occlusion(가림현상)
  : 일부분이 가려진 물체도 컴퓨터가 인식을 해내야 함 ( 마치 사람이 사과 사진에서 일부분만 보이고 나머지가 가려있다 해도 사과라고 인식하는 것처럼)
• model의 assumption을 위반할 경우 quality는 상당히 떨어짐
  - rotation > 20
  (즉, rotation이 20도 이하라면 CC 이용해도 괜찮음)
  - scale difference > 30%

---

한눈에 정리

---

참고사이트

• OpenCV - 25. 이미지 매칭 (평균 해시 매칭, 템플릿 매칭)
• What Is Cross-Correlation?
• [OpenCV Practice 14] 이미지 피라미드 (Image Pyramid)
• Scale Space와 이미지 피라미드(image pyramid)
• Scale Space와 이미지 피라미드(image pyramid)