Motivation
이 사진에서 어떻게 비슷한 지역들을 인식할 수 있을까....?
=> 즉 어떻게 group similar things할 수 있을까....!
여기서 제안되는 것은 바로 clustering이다.
clustering
: 어떤 데이터들이 주어졌을 때,
그 데이터들을 비슷한 특성을 가진 데이터들끼리 묶는 것 (= a single token)
(label이 없는 unsupervised learning)
clustering은 image processing과 image understanding에서 중요하다!
Clustering for Image Segmentation
우리는 지금 object recogization하는 것이 아니므로, 이 픽셀 그룹은 lake다~ 저 픽셀 그룹은 sky이다~라고 얘기할 필요가 없다. 그저 각각의 픽셀 그룹이 서로 다른 성격을 갖고 있기 때문에 다른 그룹으로 분류되었다 정도 !
Goal:
training data 없이 image를 similar regions로 쪼개는 것
Key Challenges in Clustering
clustering이란 비슷한 성격을 갖는 애들끼리 묶어주는 것인데
그렇다면 몇가지 의문점이 생기지
Key Challenges:
1. two data points나 areas를 similar하다고 판단하는 기준이 뭘까?
2. pairwise similarity로부터 어떻게 전체의 grouping을 계산할 수 있을까?
Mean Shift Segmentation
image data에 대하여 clustering-based segmentation을 하는 여러용도로 사용될 수 있는 기술이다.
다시 한번 강조하지만, 여기서 segmentation이 된 각각의 group은 semantic information, 즉 의미를 갖는 정보를 전혀 갖고 있지 않다. 이 그룹은 land고, 이 그룹은 lake고 이런 의미를 갖는 정보가 없다는 뜻!
Mean Shift Algorithm
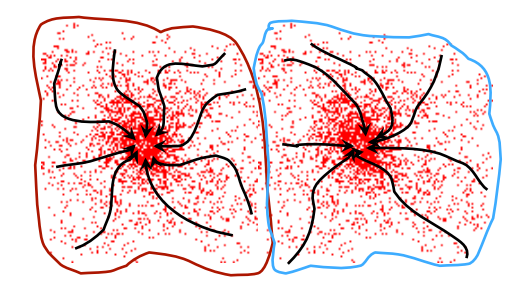
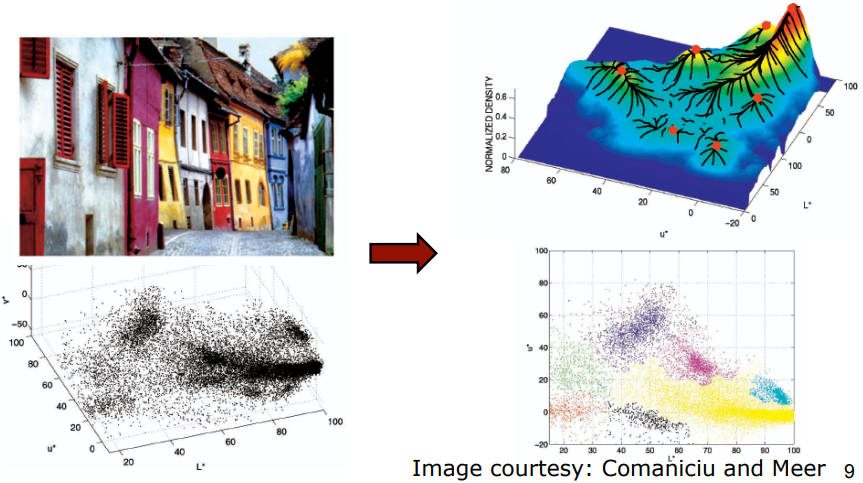다음 그림을 간단히 설명하면 이러하다. 일단 주어진 image에 대하여 그것은 density function을 정의할 수 있다. (data points가 많이 모인 곳은 높이가 높고, 그렇지 않은 곳은 낮고...) 따라서 그림을 보면, 빨간색 점 주변의 지역에서는 uphill하면 빨간색 점이 최종 도착지가 될 것이다. black line은 data point가 최종 도착지(빨간색 점)에 도달하는 과정을 표시하였다. 같은 빨간색 점으로 가는 data들은 같은 group으로 묶여지겠지.
즉 간단히 정리하면, pdf(probability density function)을 찾고, 그 안에서 maxima를 찾는 것
...
어떤 블로그에서 예시를 들어주었는데 크게 와닿는다.
시력이 매우 나쁜 사람을 산에 던져 두고 산 정상으로 찾아오라면 어떻게 될까?
당연히 그 사람은 시력이 보이는 한도 내에서는 가장 높은 곳으로 걸음을 옮기고,
또 이렇게 가다보면 산의 정상에 다다를 수 있다.
이러한 탐색 방법을 Hill Climb라고 부르는데,
Mean shift도 Hill Climb 탐색 방법의 일종이다.
...
여기서 교수님께서 강조하셨던 부분은, 반드시 uphill로 간다는 것이다.
절대로 downhill로 가지 않는다.
Mean Shift Algorithm
: KDE(Kernel Density Estimation) 방법을 이용하여 개별 데이터 포인트들이 데이터 분포가 높은 곳으로 이동하면서 군집화를 수행하는 모델
: Non-parametric(비모수) 모델이기 때문에 사전에 군집화 개수를 지정하지 않으며 데이터 분포도에 기반해 자동으로 군집화 개수를 정한다.
non-parametric 방식으로 어떻게 pdf를 찾을 수 있는 것일까......?
바로 KDE를 이용해서 pdf를 구할 수 있다.
KDE(Kernel Density Estimation)
KDE란 개별 데이터 포인트들에 커널함수를 적용한 후, 반환값들을 모두 합한 뒤에 개별 데이터 포인트들의 개수로 나누어서 확률밀도함수를 추정하는 방식
대표적인 커널함수로는 Gausssian 분포함수 (정규분포 함수) 이용
++ KDE에서
(1) Kernel의 종류 (2) bandwidth
우리가 직접 결정하는 것
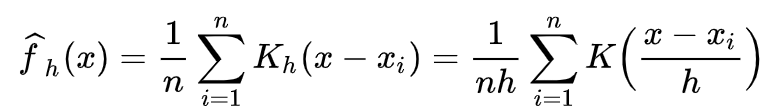각각의 기호들을 조금 이해해보자.
K: 개별 데이터를 입력시킬 Kernel 함수
h: bandwidth라고 불리는 smoothing parameter
- h값을 작게 부여할수록, undersmoothing하여 overfitting이 발생하고,
h값을 크게 부여할수록, oversmoothing하여 underfitting 발생
n: data point의 개수
수식이 아닌 그림으로 나타내면 다음과 같다.
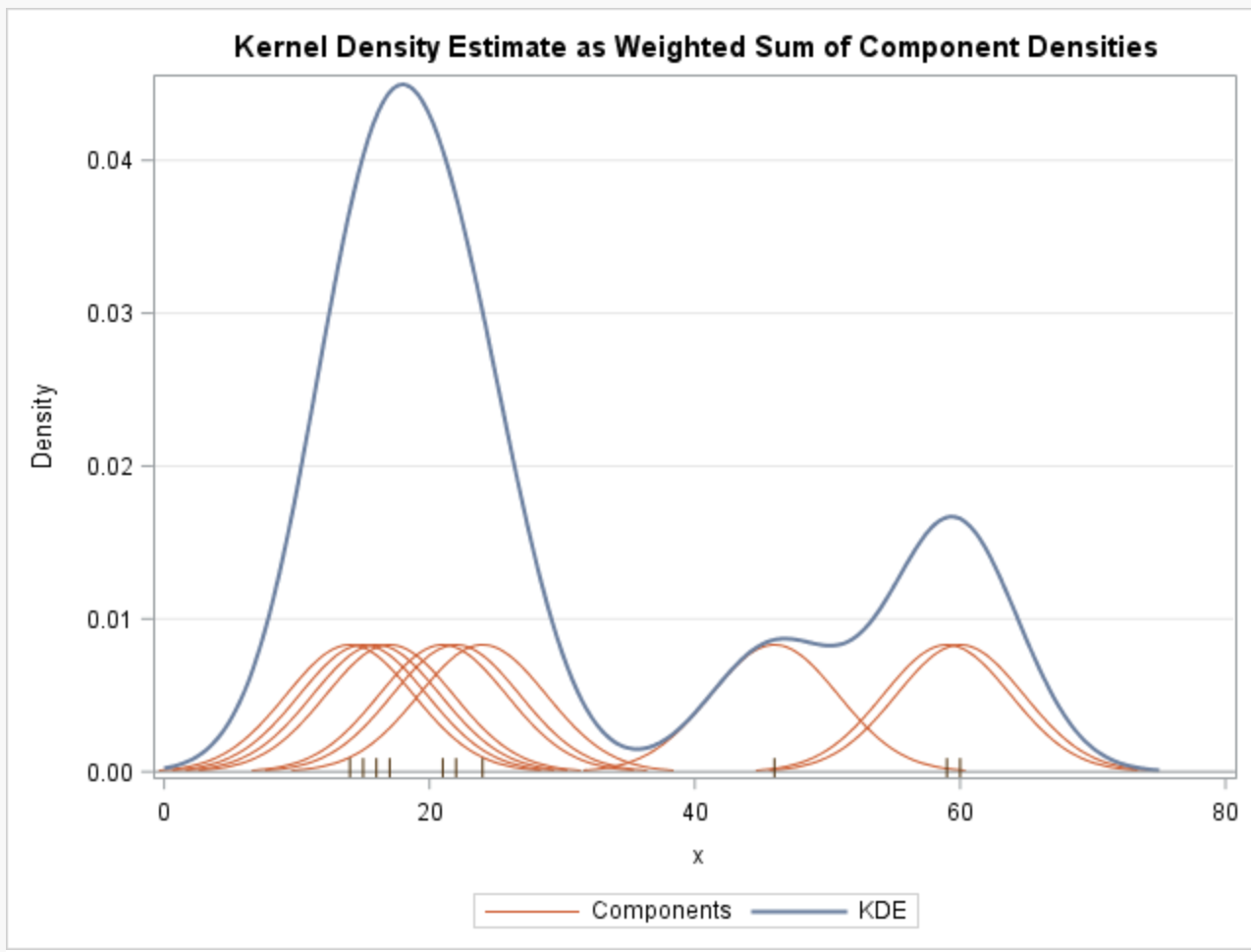빨간색의 Components가 개별 데이터 포인트들에 커널함수를 적용한 형태이고, 이를 총 데이터건수로 나누어 pdf를 추정한 것이 파란색 선의 KDE이다.
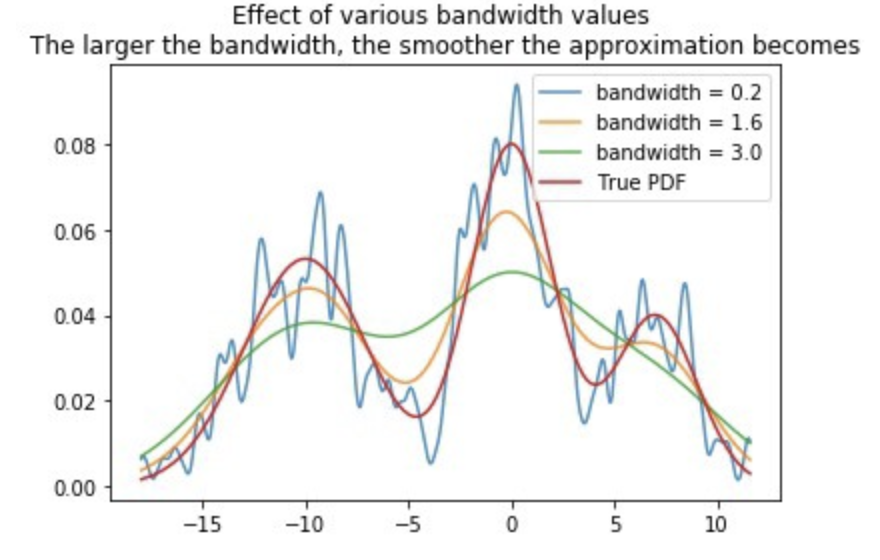bandwidth값에 따라 KDE의 분포는 변한다.
이 경우는 bandwidth값이 1.6일 때 실제 PDF와 가장 유사했다는 것을 확인할 수 있었다.
bandwidth=0.2일 때는 overfitting, bandwidth=3.0일 때는 underfitting 발생
Mean Shift
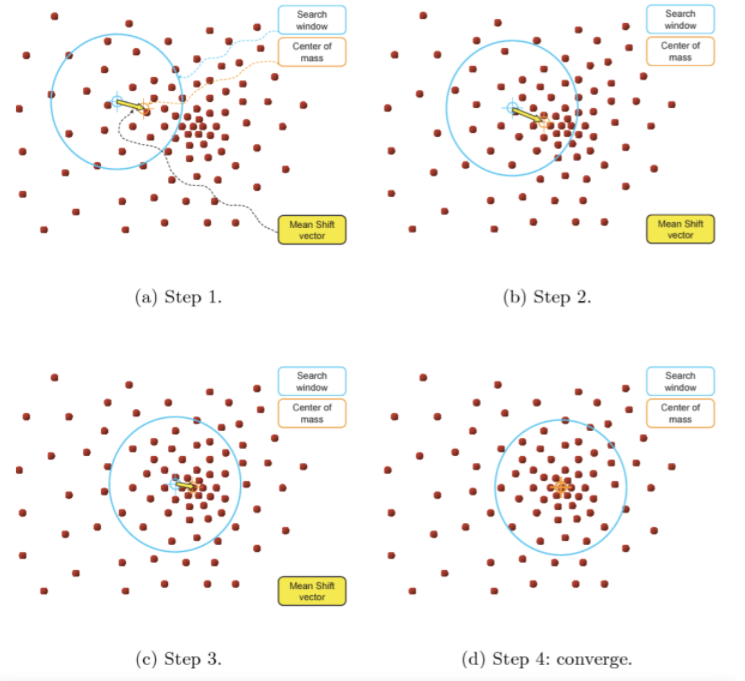개별 포인트 하나가 하늘색 동그라미 반경 내에서 데이터 분포 확률 밀도가 가장 높은 곳으로 이동한다. 이때 이동할 '밀도가 가장 높은 곳'을 찾기 위하여 데이터 포인트들과의 거리값을 Kernel 함수값으로 입력한 후 반환되는 값을 처음 위치에서 그만큼 이동하면서 위치를 업데이트한다.
(STEP1)개별 데이터의 특정 반경 내에서 주변 데이터를 포함한 데이터 분포도 pdf 계산한다.(STEP2)계산한 데이터 분포도 pdf 중 가장 밀도가 높은 방향으로 데이터 위치 이동시킨다. 이때 pdf를 찾기 위해 KDE 이용한다.(STEP3)update된 새로운 반경 내에서 STEP1과 STEP2 반복하여 위치를 업데이트한다.(STEP4)STEP3를 반복하다가 더 이상 데이터의 위치가 업데이트되지 않을 때 반복을 멈춘다.
Computing the Mean Shift
가장 밀도가 높은 방향(vector)은 어떻게 찾는 것일까?
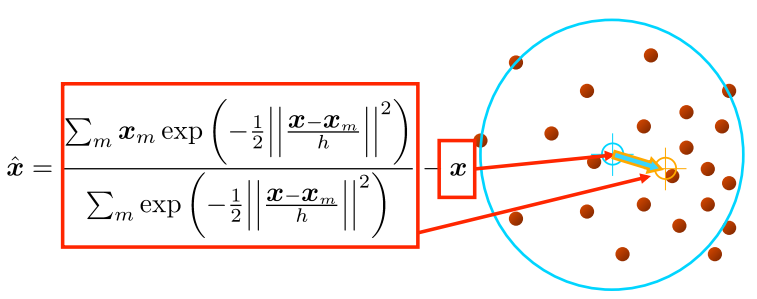
잠깐 수식이 완벽하게 이해가 안된거 같은데..
(내용추가할 것)
단순한 mean shift 과정:
- mean shift vector 계산
- Kernel window를 옮기기
Attraction Basin
Attraction basin
: 모든 궤도들이 동일한 mode로 이어지는 부분을 의미
Cluster
:한 mode의 attraction basin 안에 있는 모든 data point들
여기서 mode라는 단어를 사용했으니 이를 이용하여 다시 한번 정리를 해보자면
Mean Shift Alogrithm이란
주어진 point 집합들의 mode를 찾는 일
Segmentation by Mean Shift
mean shift는 우리가 이제 충분히 배웠으니 그럼 segmentation하는 과정을 정리해보자.
- 일단 각각의 pixel에 대하여 features를 구한다. (color, gradients, texture..)
- features의 kernel size인 K_f과 position인 K_s를 설정한다.
- 각각의 pixel 위치에 대하여 window를 초기화하면서 update한다.
- convergence될 때까지 각 window에 대하여 mean shift를 수행한다.
- 너비 K_f와 위치 K_s 안에 있는 window를 모두 합한다.
(window는 features의 개수만큼 있겠지)
다음 그림을 보면, 결과가 꽤나 잘 나온 것을 확인할 수 있음
Mean Shift Pros and Cons
Pros
- 어떤 이미지 데이터든지 적용할 수 있다.(general-practice segmentation)
- clusters의 개수와 regions의 모양에 제약이 없는 편이다.
- outlier에 굉장히 강하다.
(smoothing kernel의 역할 덕분 :D)
Cons
- 사전에 우리가 직접 kernel size를 정해야 한다. 꽤나 까다로운 작업이다.
- high-dimensional features에 대해서는 적합하지 않다.
Summary
Mean shift말고도 다양한 clustering 접근들이 있다.
- Agglomerative clustering
- k-means
- GMM estimatino
- ...
참고사이트
