
Matrix Factorization(MF) 기반 추천 알고리즘
1) 메모리 기반
추천을 위한 데이터를 모두 메모리에 갖고 추천이 필요할 때마다 이 데이터를 사용해서 계산 및 추천
Ex) Collaboratice Filtering
2) 모델 기반
데이터로부터 추천을 위한 모델 구성한 후에 이 모델만 저장하고, 실제 추천할 때에는 이 모델을 사용
Ex) Matrix Factorization(MF) : 행렬 요인화 방식, Deep Learning 방식
메모리 기반 – 개별 사용자의 데이터에 집중
모델 기반 추천 – 전체 사용자의 평가 패턴으로부터 모델을 구성 데이터의 약한신호도 더 잘 잡아냄
Weak signal – 개별 사용자의 행동분석에서는 잘 드러나지 않는 패턴
Matrix Factorization(MF) 방식의 원리
평가데이터 (사용자 * 아이템)으로 구성된 하나의 행렬을 2개의 행렬로 분해하는 방법!
K개의 잠재 요인(latent factor)
-
R : rating matrix – M명의 사용자가 N개 아이템에 대해 평가한 데이터를 포함한 2차원 행렬
MF : 이 R 행렬을 사용자 행렬(P)와 아이템행렬(Q)로 쪼개어 분석하는 방식 -
P : User latent matrix – 사용자 잠재요인 행렬(M*K)
각 사용자의 특성을 나타내는 K개 요인의 값으로 이루어진 행렬 -
Q : Item latent matirx – 아이템 잠재요인 행렬(N*K)
각 아이템의 특성을 나타내느 K개의 요인으로 이루어진 행렬
P x Qt 은 R과 같은 M*N 행렬이며 최대한 기존 R에 유사한 값을 가지도록 하는 P와 Q를 구해야함
SGD(Stochastic Gradient Descent)를 사용한 MF 알고리즘
텍스트(사용자 X 아이템)의 평잼행렬인 R로부터 P, Q 행렬을 분해하는 알고리즘의 순서
1) 잠재요인의 갯수 k를 정한다.
2) 주어진 K에 따라 P(MxK)와 Q(NxK)의 임의의 수로 채워진 행렬을 만든다.
3) P, Q 행렬을 이용하여 예측평점 Rhat = PxQt 계산
4) 실제 데이터와 R과 예측평점 Rhat을 비교하여, 오차를 구하고, 이 오차를 줄이기 위해 P,Q를 수정
5) 반복(정해진 iteration 혹은 수렴할때까지)
예측오차를 줄이는 방법으로 SGD를 활용한 P, Q 행렬 최적화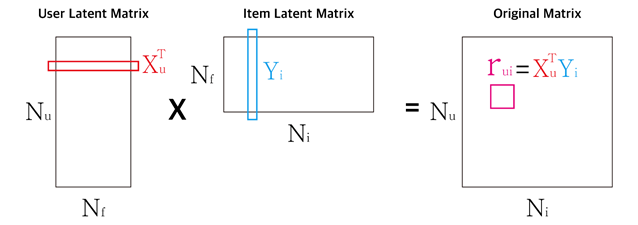 오차제곱의 최소화 유도(MSE, RMSE 등)
오차제곱의 최소화 유도(MSE, RMSE 등)

코드 1) SGD를 사용한 MF 기본 알고리즘
# MF class
class MF():
def __init__(self, ratings, K, alpha, beta, iterations, verbose=True):
self.R = np.array(ratings)
self.num_users, self.num_items = np.shape(self.R) # ratings를 numpy array로
self.K = K
self.alpha = alpha
self.beta = beta
self.iterations = iterations
self.verbose = verbose
# Root Mean Squared Error (RMSE) 계산
def rmse(self):
xs, ys = self.R.nonzero()
self.predictions = []
self.errors = []
for x, y in zip(xs, ys):
prediction = self.get_prediction(x, y)
self.predictions.append(prediction)
self.errors.append(self.R[x, y] - prediction)
self.predictions = np.array(self.predictions)
self.errors = np.array(self.errors)
return np.sqrt(np.mean(self.errors**2))
def train(self):
# Initializing user-feature and item-feature matrix
# P와 Q 행렬을 평균 0, 표준편차 1/K인 정규분포를 갖는 난수로 초기화
self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K))
self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K))
# Initializing the bias terms
self.b_u = np.zeros(self.num_users)
self.b_d = np.zeros(self.num_items)
self.b = np.mean(self.R[self.R.nonzero()])
#iteration 한번마다 평가경향을 계속 초기화시켜서 다시 계산
# List of training samples
rows, columns = self.R.nonzero()
self.samples = [(i, j, self.R[i,j]) for i, j in zip(rows, columns)]
# Stochastic gradient descent for given number of iterations
training_process = []
for i in range(self.iterations):
np.random.shuffle(self.samples)
self.sgd()
rmse = self.rmse()
training_process.append((i+1, rmse))
if self.verbose: # 10번마다 출력
if (i+1) % 10 == 0:
print("Iteration: %d ; Train RMSE = %.4f " % (i+1, rmse))
return training_process
# Rating prediction for user i and item j
def get_prediction(self, i, j):
prediction = self.b + self.b_u[i] + self.b_d[j] + self.P[i, :].dot(self.Q[j, :].T)
# 전체 평균 + 사용자 i의 평가경향 + 아이템j의 평가 경향 + r hat
return prediction
# Stochastic gradient descent to get optimized P and Q matrix
def sgd(self):
for i, j, r in self.samples:
prediction = self.get_prediction(i, j)
e = (r - prediction)
#편미분 식
self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])
self.b_d[j] += self.alpha * (e - self.beta * self.b_d[j])
self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])
self.Q[j, :] += self.alpha * (e * self.P[i, :] - self.beta * self.Q[j,:])
코드 2) train test 분리 MF 알고리즘
# train test 분리
from sklearn.utils import shuffle
TRAIN_SIZE = 0.75
ratings = shuffle(ratings, random_state=1)
cutoff = int(TRAIN_SIZE * len(ratings))
ratings_train = ratings.iloc[:cutoff]
ratings_test = ratings.iloc[cutoff:]
# New MF class for training & testing
class NEW_MF():
def __init__(self, ratings, K, alpha, beta, iterations, verbose=True):
self.R = np.array(ratings)
##### >>>>> (2) user_id, item_id를 R의 index와 매핑하기 위한 dictionary 생성
item_id_index = []
index_item_id = []
for i, one_id in enumerate(ratings):
item_id_index.append([one_id, i])
index_item_id.append([i, one_id])
self.item_id_index = dict(item_id_index)
self.index_item_id = dict(index_item_id)
user_id_index = []
index_user_id = []
for i, one_id in enumerate(ratings.T):
user_id_index.append([one_id, i])
index_user_id.append([i, one_id])
self.user_id_index = dict(user_id_index)
self.index_user_id = dict(index_user_id)
#### <<<<< (2)
self.num_users, self.num_items = np.shape(self.R)
self.K = K
self.alpha = alpha
self.beta = beta
self.iterations = iterations
self.verbose = verbose
# train set의 RMSE 계산
def rmse(self):
xs, ys = self.R.nonzero()
self.predictions = []
self.errors = []
for x, y in zip(xs, ys):
prediction = self.get_prediction(x, y)
self.predictions.append(prediction)
self.errors.append(self.R[x, y] - prediction)
self.predictions = np.array(self.predictions)
self.errors = np.array(self.errors)
return np.sqrt(np.mean(self.errors**2))
# Ratings for user i and item j
def get_prediction(self, i, j):
prediction = self.b + self.b_u[i] + self.b_d[j] + self.P[i, :].dot(self.Q[j, :].T)
return prediction
# Stochastic gradient descent to get optimized P and Q matrix
def sgd(self):
for i, j, r in self.samples:
prediction = self.get_prediction(i, j)
e = (r - prediction)
self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])
self.b_d[j] += self.alpha * (e - self.beta * self.b_d[j])
self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])
self.Q[j, :] += self.alpha * (e * self.P[i, :] - self.beta * self.Q[j,:])
##### >>>>> (3)
# Test set을 선정
def set_test(self, ratings_test):
test_set = []
for i in range(len(ratings_test)): # test 데이터에 있는 각 데이터에 대해서
x = self.user_id_index[ratings_test.iloc[i, 0]] # 사용자 인덱스
y = self.item_id_index[ratings_test.iloc[i, 1]] # 아이템 인덱스
z = ratings_test.iloc[i, 2] # 평점 인덱스
test_set.append([x, y, z])
self.R[x, y] = 0 # Setting test set ratings to 0
self.test_set = test_set
return test_set # Return test set
# Test set의 RMSE 계산
def test_rmse(self):
error = 0
for one_set in self.test_set:
predicted = self.get_prediction(one_set[0], one_set[1])
error += pow(one_set[2] - predicted, 2) # 오차 제곱의 합 누적
return np.sqrt(error/len(self.test_set))
# Training 하면서 test set의 정확도를 계산
def test(self):
# Initializing user-feature and item-feature matrix
self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K))
self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K))
# Initializing the bias terms
self.b_u = np.zeros(self.num_users)
self.b_d = np.zeros(self.num_items)
self.b = np.mean(self.R[self.R.nonzero()])
# List of training samples
rows, columns = self.R.nonzero()
self.samples = [(i, j, self.R[i,j]) for i, j in zip(rows, columns)]
# Stochastic gradient descent for given number of iterations
training_process = []
for i in range(self.iterations):
np.random.shuffle(self.samples)
self.sgd() # sgd로 업데이트
rmse1 = self.rmse()
rmse2 = self.test_rmse()
training_process.append((i+1, rmse1, rmse2))
if self.verbose:
if (i+1) % 10 == 0:
print("Iteration: %d ; Train RMSE = %.4f ; Test RMSE = %.4f" % (i+1, rmse1, rmse2))
return training_process
# Ratings for given user_id and item_id
def get_one_prediction(self, user_id, item_id):
return self.get_prediction(self.user_id_index[user_id], self.item_id_index[item_id])
# Full user-movie rating matrix
def full_prediction(self):
return self.b + self.b_u[:,np.newaxis] + self.b_d[np.newaxis,:] + self.P.dot(self.Q.T)
# Testing MF RMSE
R_temp = ratings.pivot(index='user_id', columns='movie_id', values='rating').fillna(0)
mf = NEW_MF(R_temp, K=30, alpha=0.001, beta=0.02, iterations=100, verbose=True)
test_set = mf.set_test(ratings_test)
result = mf.test()
# Printing predictions
print(mf.full_prediction())
print(mf.get_one_prediction(1, 2)) 코드 3) 최적의 파라미터 찾기
# New MF class for training & testing
class NEW_MF():
def __init__(self, ratings, K, alpha, beta, iterations, verbose=True):
self.R = np.array(ratings)
##### >>>>> (2) user_id, item_id를 R의 index와 매핑하기 위한 dictionary 생성
item_id_index = []
index_item_id = []
for i, one_id in enumerate(ratings):
item_id_index.append([one_id, i])
index_item_id.append([i, one_id])
self.item_id_index = dict(item_id_index)
self.index_item_id = dict(index_item_id)
user_id_index = []
index_user_id = []
for i, one_id in enumerate(ratings.T):
user_id_index.append([one_id, i])
index_user_id.append([i, one_id])
self.user_id_index = dict(user_id_index)
self.index_user_id = dict(index_user_id)
#### <<<<< (2)
self.num_users, self.num_items = np.shape(self.R)
self.K = K
self.alpha = alpha
self.beta = beta
self.iterations = iterations
self.verbose = verbose
# train set의 RMSE 계산
def rmse(self):
xs, ys = self.R.nonzero()
self.predictions = []
self.errors = []
for x, y in zip(xs, ys):
prediction = self.get_prediction(x, y)
self.predictions.append(prediction)
self.errors.append(self.R[x, y] - prediction)
self.predictions = np.array(self.predictions)
self.errors = np.array(self.errors)
return np.sqrt(np.mean(self.errors**2))
# Ratings for user i and item j
def get_prediction(self, i, j):
prediction = self.b + self.b_u[i] + self.b_d[j] + self.P[i, :].dot(self.Q[j, :].T)
return prediction
# Stochastic gradient descent to get optimized P and Q matrix
def sgd(self):
for i, j, r in self.samples:
prediction = self.get_prediction(i, j)
e = (r - prediction)
self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])
self.b_d[j] += self.alpha * (e - self.beta * self.b_d[j])
self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])
self.Q[j, :] += self.alpha * (e * self.P[i, :] - self.beta * self.Q[j,:])
##### >>>>> (3)
# Test set을 선정
def set_test(self, ratings_test):
test_set = []
for i in range(len(ratings_test)): # test 데이터에 있는 각 데이터에 대해서
x = self.user_id_index[ratings_test.iloc[i, 0]]
y = self.item_id_index[ratings_test.iloc[i, 1]]
z = ratings_test.iloc[i, 2]
test_set.append([x, y, z])
self.R[x, y] = 0 # Setting test set ratings to 0
self.test_set = test_set
return test_set # Return test set
# Test set의 RMSE 계산
def test_rmse(self):
error = 0
for one_set in self.test_set:
predicted = self.get_prediction(one_set[0], one_set[1])
error += pow(one_set[2] - predicted, 2)
return np.sqrt(error/len(self.test_set))
# Training 하면서 test set의 정확도를 계산
def test(self):
# Initializing user-feature and item-feature matrix
self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K))
self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K))
# Initializing the bias terms
self.b_u = np.zeros(self.num_users)
self.b_d = np.zeros(self.num_items)
self.b = np.mean(self.R[self.R.nonzero()])
# List of training samples
rows, columns = self.R.nonzero()
self.samples = [(i, j, self.R[i,j]) for i, j in zip(rows, columns)]
# Stochastic gradient descent for given number of iterations
training_process = []
for i in range(self.iterations):
np.random.shuffle(self.samples)
self.sgd()
rmse1 = self.rmse()
rmse2 = self.test_rmse()
training_process.append((i+1, rmse1, rmse2))
if self.verbose:
if (i+1) % 10 == 0:
print("Iteration: %d ; Train RMSE = %.4f ; Test RMSE = %.4f" % (i+1, rmse1, rmse2))
return training_process
# Ratings for given user_id and item_id
def get_one_prediction(self, user_id, item_id):
return self.get_prediction(self.user_id_index[user_id], self.item_id_index[item_id])
# Full user-movie rating matrix
def full_prediction(self):
return self.b + self.b_u[:,np.newaxis] + self.b_d[np.newaxis,:] + self.P.dot(self.Q.T)
# 최적의 K값 찾기
results = []
index = []
for K in range(50, 261, 10):
print('K =', K)
R_temp = ratings.pivot(index='user_id', columns='movie_id', values='rating').fillna(0)
mf = NEW_MF(R_temp, K=K, alpha=0.001, beta=0.02, iterations=300, verbose=True)
test_set = mf.set_test(ratings_test)
result = mf.test()
index.append(K)
results.append(result) K = 50
Iteration: 10 ; Train RMSE = 0.9661 ; Test RMSE = 0.9834
Iteration: 20 ; Train RMSE = 0.9414 ; Test RMSE = 0.9644
Iteration: 30 ; Train RMSE = 0.9304 ; Test RMSE = 0.9566
.
.
.
Iteration: 260 ; Train RMSE = 0.6256 ; Test RMSE = 0.9256
Iteration: 270 ; Train RMSE = 0.6067 ; Test RMSE = 0.9286
Iteration: 280 ; Train RMSE = 0.5887 ; Test RMSE = 0.9317
Iteration: 290 ; Train RMSE = 0.5716 ; Test RMSE = 0.9350
Iteration: 300 ; Train RMSE = 0.5554 ; Test RMSE = 0.9384
K = 60
Iteration: 10 ; Train RMSE = 0.9662 ; Test RMSE = 0.9834
Iteration: 20 ; Train RMSE = 0.9416 ; Test RMSE = 0.9644
Iteration: 30 ; Train RMSE = 0.9307 ; Test RMSE = 0.9566
.
.
.
Iteration: 280 ; Train RMSE = 0.5882 ; Test RMSE = 0.9261
Iteration: 290 ; Train RMSE = 0.5692 ; Test RMSE = 0.9290
Iteration: 300 ; Train RMSE = 0.5511 ; Test RMSE = 0.9321
K = 70
Iteration: 10 ; Train RMSE = 0.9662 ; Test RMSE = 0.9834
Iteration: 20 ; Train RMSE = 0.9416 ; Test RMSE = 0.9644
.
.
Iteration: 240 ; Train RMSE = 0.6763 ; Test RMSE = 0.9154
Iteration: 250 ; Train RMSE = 0.6538 ; Test RMSE = 0.9170
Iteration: 260 ; Train RMSE = 0.6316 ; Test RMSE = 0.9191
Iteration: 270 ; Train RMSE = 0.6101 ; Test RMSE = 0.9215
Iteration: 280 ; Train RMSE = 0.5892 ; Test RMSE = 0.9241
Iteration: 290 ; Train RMSE = 0.5691 ; Test RMSE = 0.9268
Iteration: 300 ; Train RMSE = 0.5498 ; Test RMSE = 0.9297

글 정말 잘 읽었습니다. 질문 드리고 싶은 것이 있는데요 ..
1) Rating 데이터에서 Train 데이터와 Test 데이터를 나눴는데, Train 데이터는 활용하지 않는데, 특별한 이유가 있는 건가요 ?