ML 2) Linear Regression, Gradient Descen
ML 포스팅은 한학기동안 머신러닝 스터디를 하며 공부한 내용을 바탕으로 하였으며,

O’Reilly Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition을 기반으로 하고 있습니다.
1편) What is Machine Learning?
2편) Linear Regression, Gradient Descent
3편) Regularization, Logistic Regression
4편) SVM
5편) Decision Tree
6편) Ensemble
7편) Dimension Reduction
이번 파트 제일 초반에 책에서 언급한 내용이 정말 인상적이라 포스팅 초반에 언급을 하려고 합니다! 사실 요새는 scikit-learn, Tensorflow 같은 프레임워크가 워낙 잘돼있어서, 코드한줄로 모델을 사용하는 건 어렵지가 않은 것 같습니다. 하지만 적절한 모델 사용, train 방식 선택, 하이퍼파라미터 튜닝, 디버깅, 에러분석을 위해 모델의 원리에 대한 이해는 필수적이기 때문에 구체적이고 세세한 원리까지 파고들어 공부하는 것이 정말 중요하다고 하네요! 처음 공부를 시작할때보다 많이 헤이해졌는데 다시 마음을 다잡아야 겠습니다.... 다시 본문으로 돌아와 선형회귀와 경사하강법에 대해 정리해보도록 하겠습니다.
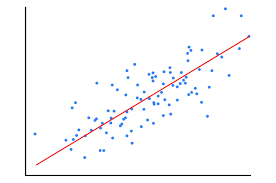
데이터셋(train dataset)을 가장 잘 표현하는 직선(Linear Regression)식에 가장 적합한 파라미터를 찾아야하며, 이때 사용하는 방식으로 정규방정식, 경사하강법이 존재합니다.
Linear Regression Model(선형회귀 모델)
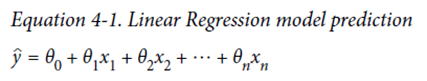
일반적인 선형 모델 : 입력 특성의 가중치 합과 편향(bias, 상수)를 더해 예측
ŷ – 예측값(predicted value)
θ0 = bias
θ1 , θ2 , θ3 …. 가중치

선형 회귀 모델의 예측(벡터 형태)
Θ - 편향 θ0와 θ1 , θ2 , θ3 ….의 특성 가중치를 담은 모델의 파라미터 벡터
X는 X0에서 Xn까지의 샘플의 특성 벡터(feature vector), X0 은 항상 1
h0(x) – 가설(hypothesis) 함수, 모델 파라미터 θ 사용
성능 측정 지표
회귀 문제에서의 전형적인 성능지표는 평균제곱근오차(RMSE)
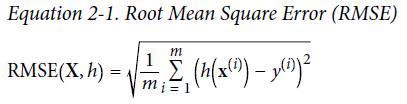
이상치가 많은 데이터의 경우 평균절대오차(MAE)를 사용하기도 함
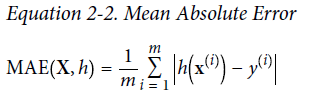
Cost function으로 MAE 대신 RMSE, MSE를 사용하는 이유
1) 오차를 더욱 증폭 -> 오차를 줄이기에 더 유리함(GD할 때 2차함수의 형태 사용 가능)
2) 시간복잡도의 개념 -> 절댓값을 사용하면 메모리에서 내부적으로 조건문을 통해서 + 값으로 보정
조건문 없이 바로 제곱을 해주는게 연산의 시간적 효율성 측면에서도 유리함!
정리
선형회귀 –샘플과 예측값의 관계를 가장 잘 표현하는 직선을 찾는 것!(=loss function을 최소화하는 모델 파라미터) 도출해야함
직선의 방정식을 구하기 위해선 기울기값과 편향을 알아야 하며, 이 기울기값, 편향 이 2가지 파라미터를 알아내기 위한 방법으로 정규방정식과 경사하강법이 존재함
1) 정규방정식(Normal Equation)
– 행렬 연산으로 cost function을 최소화하는 θ를 찾는 해석적 방법
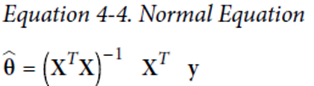
Θhat – 비용함수를 최소화 하는 θ값


장점) 해석적으로 계산하는 가장 정확하게 파라미터를 계산할 수 있는 접근 방식!
단점) 컴퓨팅자원의 한계
램에 모든 샘플을 올린 후에 계산 -> 메모리 크기가 보장되는 한정적인 상황을 제외하고는 사용의 어려움
정규방정식의 시간복잡도는 O(n^2.4) ~ O(n^3)
소규모 샘플인 경우에는 빠르게 계산이 가능하나, 샘플의 수가 커질수록 기하학적으로 계산시간이 증가함
추가로 이번 여름방학 계절학기 수업으로 선형대수를 들은 보람을 조금이라도 남기기 위해, 정규방정식에 대한 기하적 접근을 해보고자 합니다...

The Best Approximation Theorem

이 정리를 통해 어떤 부분공간 W에서 R^n의 벡터 y와의 거리차이(error)가 가장 작은 벡터는 W에 y를 정사영 시킨 벡터 yhat이며, 이를 확장시키면, Ax = b라는 식에서 b가 Col(A)에 속하지 않는 경우(해가 존재하지 않는 경우) 식을 완전히 만족하는 해는 구하지 못하더라도, 그해에 가장 근사하는 해를 구할 수 있습니다.
유일 최소제곱해 Xhat 유도공식

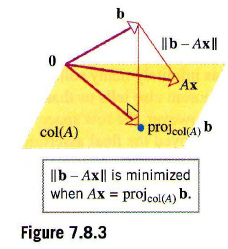
똑같은 식이더라도 편미분 or 기하적 접근을 통해서 같은 공식이 유도됨이 굉장히 흥미로웠다...
2) 경사하강법(Gradient Descent)
반복해서 파라미터를 조정해가며 cost function을 조정해나가는 가장 일반적인 방식
(Random initialization) – 임의의 값으로 설정한 파라미터 벡터 θ
에 대해 비용함수의 현재 gradient를 계산하고, 그 gradient가 감소하는 방향으로 0에 수렴할 때까지
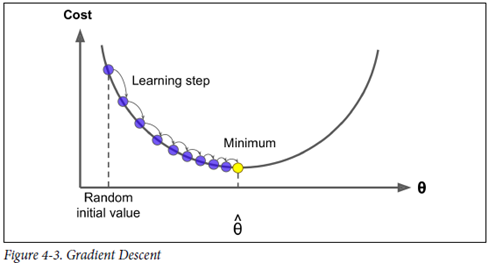
학습스텝의 크기 -> 비용 함수의 기울기에 비례함
즉, 파라미터가 최솟값에 가까울수록 스텝크기가 점진적으로 줄어듬.
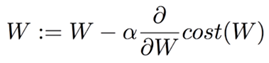
Cost function을 θ j(W)에 대해 편미분하면, 현재 W 위치에서의 접선의 기울기
하이퍼파라미터 α: learning rate
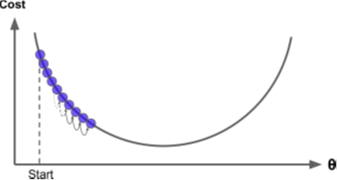
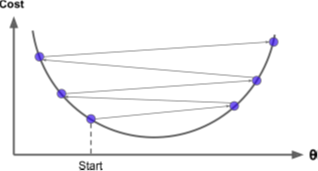
Learning rate는 환경에 따라서 적합한 값이 달라지기 때문에 일반적으로 0.01로 설정
학습을 해본 후 결과가 발산 한다면 보다 작은 값을, 학습하는데 너무 많은 시간이 소요된다면 큰 값으로 설정
MSE의 Gradient descent의 경우 convext function(=2차함수)이기 때문에 적절한 learning rate & 학습에 충분한 시간 -> global minimum에 수렴 보장
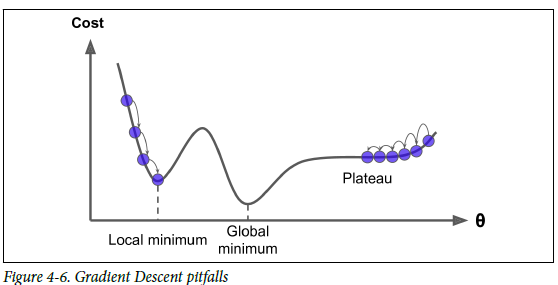
Random initialization -> local minimun 혹은 Plateau에 빠질 수 있는 문제
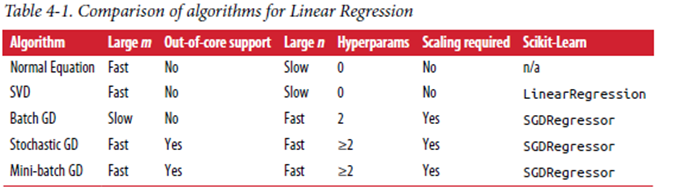
1) 배치 경사 하강법(BGD, Batch Gradient Descent)
전체 학습 데이터를 하나의 배치(크기가 n)로 묶어 학습시키는 경사하강법
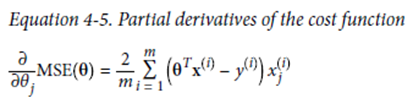
Cost function을 θ j(W)에 대해 편미분하면, 현재 W 위치에서의 접선의 기울기
<유도식>
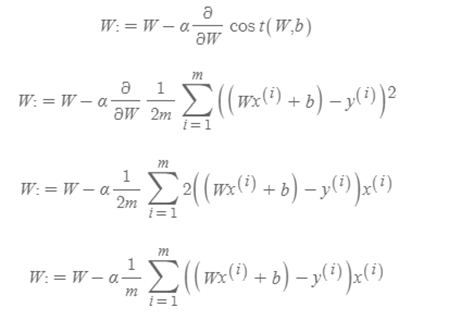

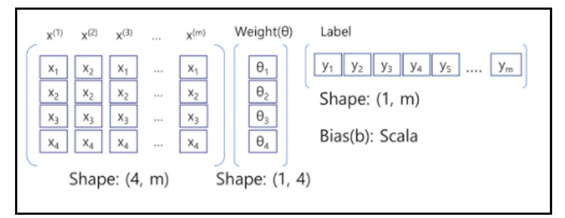
< MSE의 행렬 전환을 위한 행렬 형태 정의>
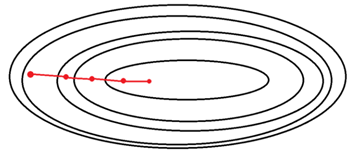
(장점)
전체 학습데이터에 대해 한번의 업데이트가 이뤄지기 때문에 수렴이 안정적으로 진행
(단점)
한 step에 모든 학습데이터를 사용하기 때문에 긴 학습시간, 메모리 소요 큼
Local minimum 해결 불가능
2) 확률적 경사하강법(SGD, Stochastic Gradient Descent)
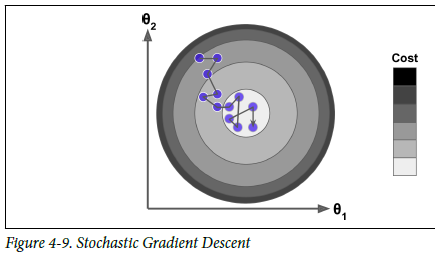
전체 데이터 중 무작위로 선정된 하나의 데이터를 이용하여 경사 하강법 1회 진행
학습 epoch 당 개별 데이터에 대해 미분을 수행하기 때문에 기울기의 방향이 매번 크게 바뀌지만, 결국 학습 데이터 전체에 대해 보편적으로 수렴(최저치로 수렴은 어려움)
장점)
빠른 연산속도, 불규칙성으로 local minimum을 건너뛰어 BGD에 비해 Global minimum에 접근할 확률이 높음
단점)
한번에 하나 데이터로 연산 -> GPU의 병렬처리를 제대로 활용 X
안정적인 수렴의 어려움
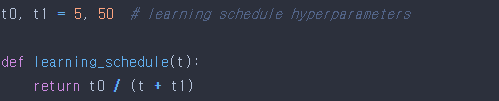
해결방안 -> 학습률을 점진적으로 감소시키는 learning schedule값을 설정하여 해결 가능
하이퍼파라미터 learning schedule
즉, 시작할때는 학습률을 크게 하여 local minimum에 빠질 위험을 줄이고, 학습이 진행됨에 따라 점차 작게 줄여서 Global minimum에 수렴할 가능성을 높이는 방식
3. 미니배치 경사하강법(MSGD, Mini-Batch Stochastic Gradient Descent)
SGD와 BGD의 절충안 -> 전체 데이터를 batch_size개씩 나눠 배치로 학습
전체 데이터셋에서 뽑은 mini-batch 안의 데이터 m개에 대해서 각 데이터에 대한 기울기를 m개 구한뒤, 그것들의 평균 기울기를 통해 모델을 업데이트 하는 방식
GPU를 이용하여 효율적으로 행렬연산을 할 수 있음
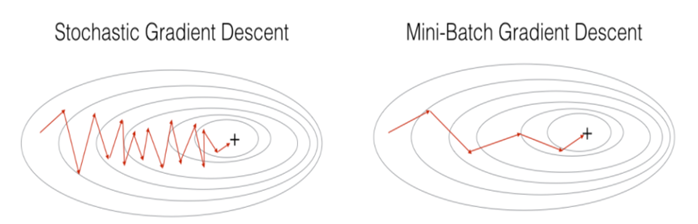
장점)
BGD보다 local minimum에 빠질 리스크가 적음
SGD보다 덜 불규칙적
M : 훈련 샘플 수 N : 특성 수