ML 7) Dimension Reduction
ML 포스팅은 한학기동안 머신러닝 스터디를 하며 공부한 내용을 바탕으로 하였으며,
O’Reilly Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition을 기반으로 하고 있습니다.
1편) What is Machine Learning?
2편) Linear Regression, Gradient Descent
3편) Regularization, Logistic Regression
4편) SVM
5편) Decision Tree
6편) Ensemble
7편) Dimension Reduction
Curse of dimension
- 고차원 dataset은 매우 희박할 위험, 긴 training 시간
차원축소를 위한 접근 방법 - 투영(projection)
대부분의 feature들은 모든 차원에 걸쳐 있지 않음
-> 고차원안의 특정 저차원 부분 공간에 밀집해있음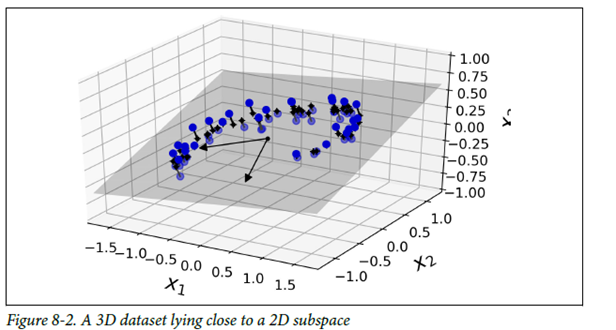
대부분의 sample들이 3차원 공간 내에 평면 형태로 놓여 있음
- 3차원 공간에 있는 2차원 부분 공간
이러한 sample들을 샘플과 평면 사이의 가장 짧은 직선을 따라 투영하여 2D 데이터셋을 얻을 수 있음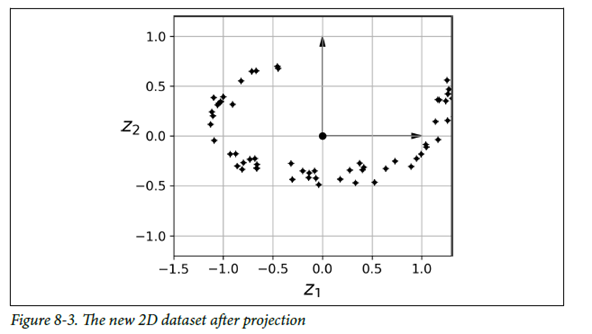
- 매니폴드 학습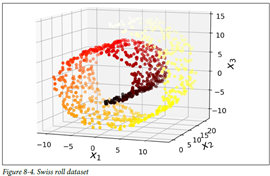
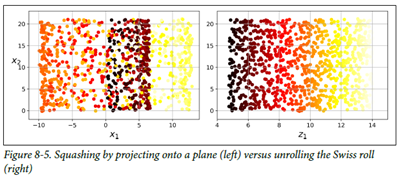
그림 4의 데이터처럼 부분 공간이 뒤틀리거나, 휘어있는 경우가 다수 존재함
단순한 Projection을하게되면 왼쪽의 그래프의 결과를 얻게 되기 때문에, dataset에 매니폴드 학습(manifold learning)을 통해서 오른쪽 그래프의 결과를 도출해내는 것
(고차원 데이터셋이 더 낮은 저차원 manifold에 가깝게 놓여 있다는 매니폴드 가정, 가설에 근거함)
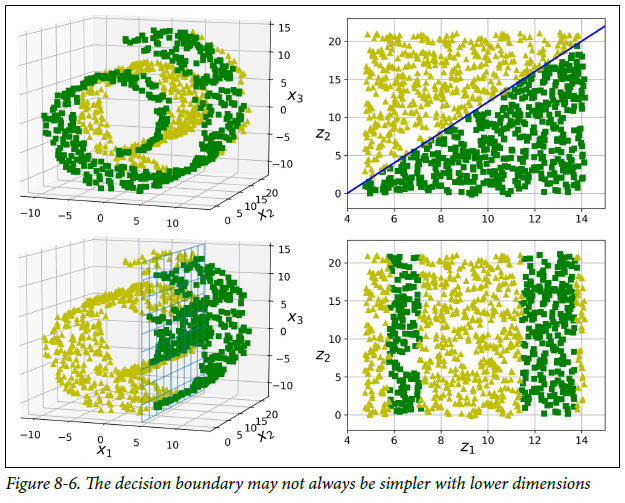Train dataset의 차원을 감소시키면 훈련 속도는 빨라지지만, 항상 더 나은 결과로 귀결되는 것은 아님!
PCA
주성분 분석 (Principal component analysis)
데이터에 가장 가까운 초평면(hyperplane)을 정의한 후, 데이터를 이 평면에 투영함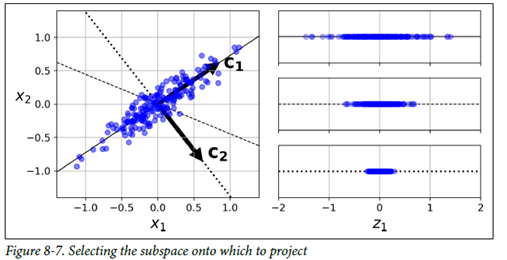
그럼 어떻게 적절한 Hyperplane을 정의할 수 있을까??
실선 투영 – 분산을 최대로 보존
점선 – 분산을 매우 적게 보존
- 분산을 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실되는 방향!
- 즉, 원본 데이터셋과 투영된 데이터 사이의 평균 제곱거리를 최소화하는 축을 선택하자!
PCA process
1) 분산이 최대인 축을 도출
2) 첫번째 축에 직교하면서 남은 분산을 최대한 보존하는 두번째 축을 찾음
3) 1,2번의 과정을 반복하며 n번째 축까지 찾아냄
-> i번째 축을 이 데이터의 i번째 주성분(principal component)라고 부름
주성분(i-1번째 축에 직교하면서, 분산을 최대로 보존하는 i번째 축)을 찾는 방법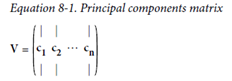
SVD(Singular value decomposition, 특이값 분해)를 통해 훈련 세트 행렬 X를, 3개 행렬의 행렬 곱셈으로 분리
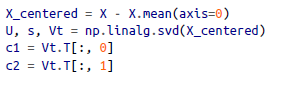주성분 추출
d차원으로 투영
주성분 추출후에는 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소
초평면에 훈련 세트를 투영하고, d차원으로 축소된 데이터셋을 얻기 위해서는
행렬 X와 V의 첫d열로 구성된 행렬 Wd를 행렬 곱셈
from sklearn.decompostion import PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)
변수에 저장된 주성분의 설명 된분산의 비율을 통해, 각 주성분 축을 따라 있는 데이터셋의 분산비율 확인
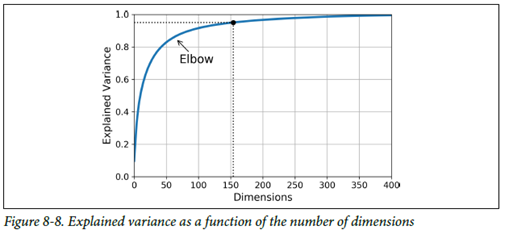이후, 충분한 분산을 가지게 될때까지 적절한 축소할 차원수를 선택
Kernal PCA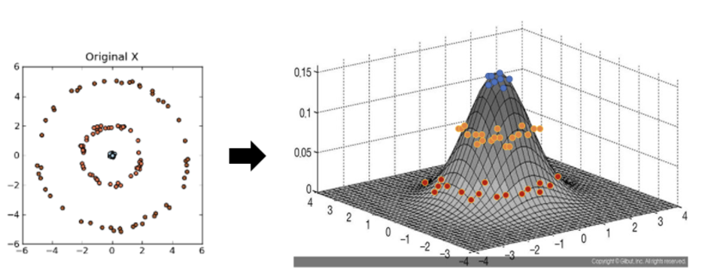
커널 트릭
비선형 함수인 커널함수를 이용하여 비선형 데이터를 고차원 공간으로 매핑하는 기술
원본 공간에서는 복잡한 비선형 결정 경계 == 고차원 특성 공간에서의 선형 결정 경계
같은 기법을 PCA에 적용
- 커널함수를 이용해 데이터를 고차원 공간으로 매핑 후 PCA 수행
- PCA : 주어진 데이터셋을 linear 벡터 형식의 주성분 분석을 통해 새로운 basis에 projection 시키는 과정
- 데이터의 주성분 분석에 kernal 함수를 이용하여 기존의 non-linear한 projection이 가능함.
- 차원축소를 위한 projection에 kernal을 사용 (kernal을 통한 차원축소의 개념)
어떤 Kernal가 하이퍼파라미터를 선택해야 할까?
1) Dimension Reduction -> 비지도 학습 : 성능 측정 기준??
차원 축소 자체가 지도 학습의 전처리 단계에서 사용되기 때문에, 주어진 문제에서의 성능이 가장 좋은 Kernal과 Hyperparameter를 선택!
2) 가장 낮은 재구성 오차를 만드는 Kernal과 Hyperparameter를 선택
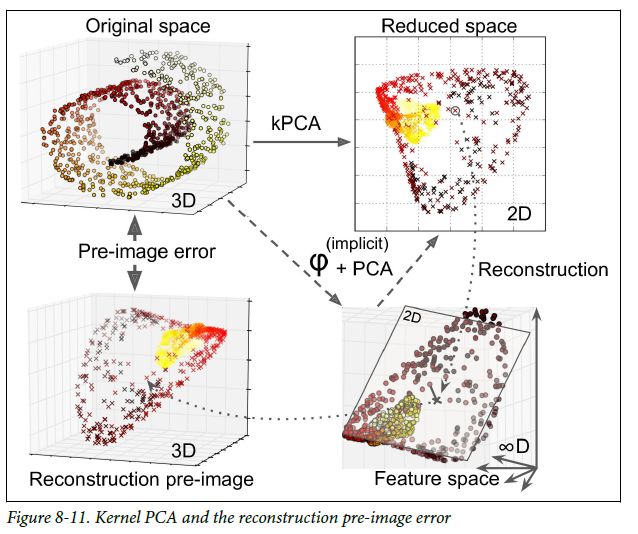1) 원본 3D 데이터셋
2) RBF 커널의 kPCA를 적용한 2D 데이터셋
3) 재구성된 3D 데이터셋
4) 무한차원의 특성공간에 매핑 후 2D로 투영
재구성의 어려움
- 재구성된 포인트에 가깝게 매핑된 원본 공간의 포인트를 찾는 방식 - 재구성 원상(pre-image)
- 재구성 원상의 오차를 최소화하는 커널과 하이퍼 파라미터 선택
rbf_pca = KernelPCA(n_components = 2, kernel='rbf', gamma=0.0433, fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)