[Compression] Learned Image Compression with Mixed Transformer-CNN Architectures 리뷰
Image Compression
논문 제목
Learned Image Compression with Mixed Transformer-CNN Architectures (CVPR 2023 Highlight)
URL: https://arxiv.org/abs/2303.14978
인용수 : 135회 (24.10.07 기준)
요약
- 대부분의 LIC(Learned Image Compression) 연구는 CNN 기반 또는 Transformer 기반으로, 각각의 장점을 가지고 있다. - 각각의 장점을 효과적으로 결합하는 방법에 대해 연구할 가치가 있음.
- CNN의 local modeling ability와 Transformer의 non-local modeling ability를 통합하는 효율적인 병렬 Transformer-CNN(TCM) 블록을 제안.
- channel squeezing를 이용한 parameter-efficient swin-transformer-based attention (SWAtten) module을 이용한 channel-wise entropy model을 제안.
Proposed Method
Problem Formulation
Channel-wise 엔트로피 모델을 사용한 이미지 압축 모델은 아래 수식으로 나타낼 수 있다.
비트스트림을 생성하기 위해, 잠재표현 y의 확률 분포를 모델링하고, 그 결과를 엔트로피 모델을 통해 효율적으로 부호화한다. 기존 연구를 바탕으로 잠재표현 y에서 평균 를 빼고 양자화한 후 다시 평균을 더하는 방식이 엔트로피 모델의 성능을 크게 향상 시킨다고 한다.
양자화된 값은 single Gaussian distribution로 모델링되며, 분산 와 함께 비트스트림으로 인코딩 되어 디코더로 전달된다.
전반적인 파이프라인에서 는 channel-wise 엔트로피 모델로부터 유도된다.
이전 연구들처럼 잠재표현 y를 동일한 크기의 슬라이스로 나누어 이후 슬라이스 인코딩의 성능을 높이는데 사용.
아래 수식으로 나타낼 수 있다.
는 Hyperprior Encoder를 나타낸다. Hyperprior는 잠재표현 y의 spatial dependency를 캡처한다.
는 모델의 예측에 필요한 평균, 스케일을 복원하는데 사용.
는 양자화 사용으로 발생하는 quantization error ()를 줄이는 데 사용.
훈련을 위한 손실함수는 Lagrangian multiplierbased rate-distortion optimization을 사용.
는 Rate-Distortion을 제어하는 파라미터.
Transformer-CNN Mixture Blocks
- Vision Transformer의 발전과 함께, ViT기반으로 이미지압축 연구를 진행하였고, CNN 기반 방법을 능가함. -> Transformer는 non-local information를 캡처하는 것이 가능하기 때문.
- non-local information이 이미지 압축 성능을 향상시킬 있음이 밝혀졌지만, local information 또한 여전이 중요한 영향을 준다.
- CNN은 local, Transformer는 non-local 정보를 처리할 수 있기에 본 논문에서는 residual network와 Swin-Transformer (SwinT) block을 결합하여 두 모델의 장점을 모두 활용하고자함.
- 이를 바탕으로 efficient parallel transformer-CNN mixture(TCM) block을 제안하였음.
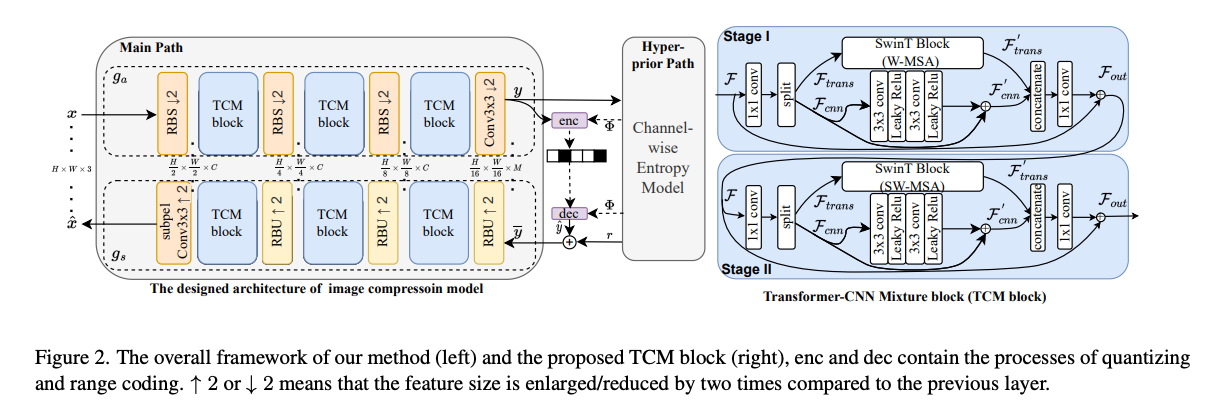
TCM 블럭의 핵심적인 특징은 입력 텐서를 로 절반씩 나눠서 계산한다.
이를 통해 모델 복잡성을 줄일 수 있고, local & non-local 피쳐를 독립적으로 병렬처리가 가능하여 더 나은 추출이 가능하다.
TCM의 수식은 아래와 같다.

논문에서 TCM 블록이 local & non-local 정보를 계산하는지 알기 위해서 Effective Receptive Fields (ERF)을 통해
ERF는 absolute gradients of a pixel in the output 즉 ,output 픽셀의 절대 기울기로 계산했다고 정의하였다.
threshold는 (0.01, 0.0001)로 잡고 기울기 값을 클리핑했다고 하며, 이를 위 이미지처럼 시각화했다고 한다.
- t=0.01일 때, TCM 기반 모델과 CNN 기반 모델의 기울기 값이 트랜스포머 기반 모델보다 작다는 것을 보였다.
- t=0.0001일 때, ERF는 트랜스포머 기반 모델처럼 먼 거리에서도 정보를 캡처할 수 있음을 보였다.
- 또한 t=0.0001일 때, CNN 기반 모델은 원형 ERF를 보이는 반면, TCM 블록은 컨텍스트에 가까운 ERF를 보였습니다.
이를 통해 TCM 블록이 local & non-local 정보를 모두 효율적으로 캡처함을 증명함.
Proposed Entropy Model
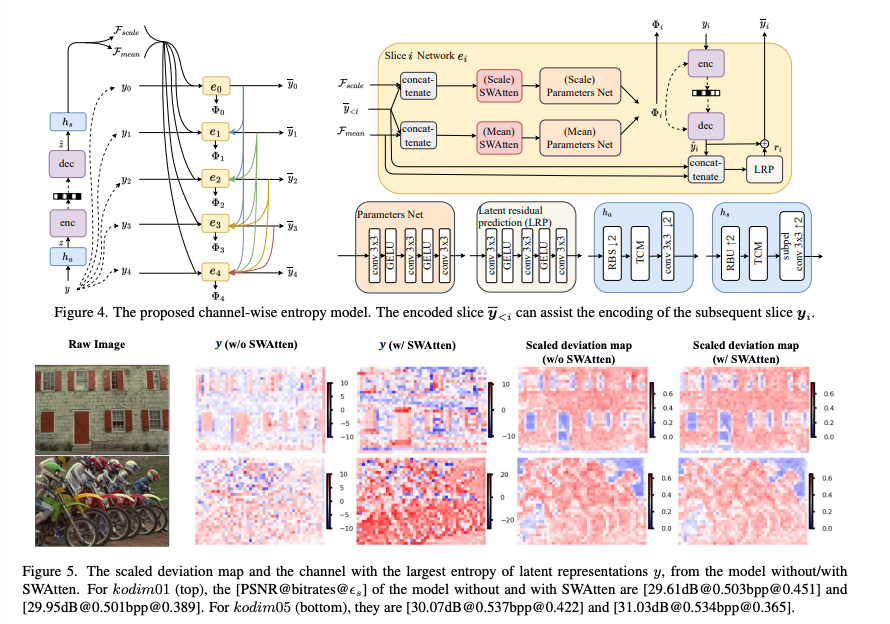
엔트로피 모델에서는 channel-wise auto-regressive entropy model을 base로 사용하였고,channel squeezing을 사용한 parameter-efficient swin-transformer-based attention module(SWAtten)을 제안했다.
SWAtten Module
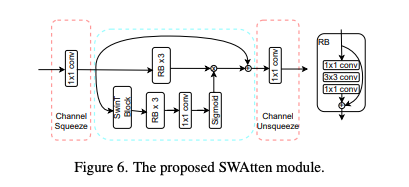
- 이전 연구(컨볼루션 기반 어텐션 등)으로 Attention Module이 이미지 압축 성능을 향상시키는 데 효과적임을 입증.
- 하지만 시간이 많이 소요되고, local 정보만 캡처한다는 문제가 있음. 해당 논문에서 인코더-디코더에 포함된 케이스가 있다.
연구에서 엡실론 (=mean absolute pixel deviation)을 통해 압축과정에서 정보 손실을 분석하는데 사용했다.
공식은 아래와 같다.
이 수식은 모델 간의 편차를 비교하데는 부정확할 수 있다고 한다. 왜냐하면 와 가 다른 범위를 가지기 때문이다. 이 편차는 y와 관련이 있기에
위 공식과 같은 스케일링 계수 감마를 도입했다.
이제 모델간의 mean absolute pixel deviation은 아래 수식으로 정의할 수 있다.
Figure 5를 보면 SWAtten 모듈을 사용했을 때와 사용하지 않았을 때의 Kodak이미지를 살펴보면, SWAtten을 사용하지 않은 모델은 가 0.451과 0.422이고, SWAtten을 사용한 모델은 가 0.389와 0.365로 줄어든 수치를 보였다.
즉, SWAtten이 deviation이 더 작기 때문에 정보 손실이 더 적고, 더 높은 품질의 이미지를 얻을 수 있다.
Result
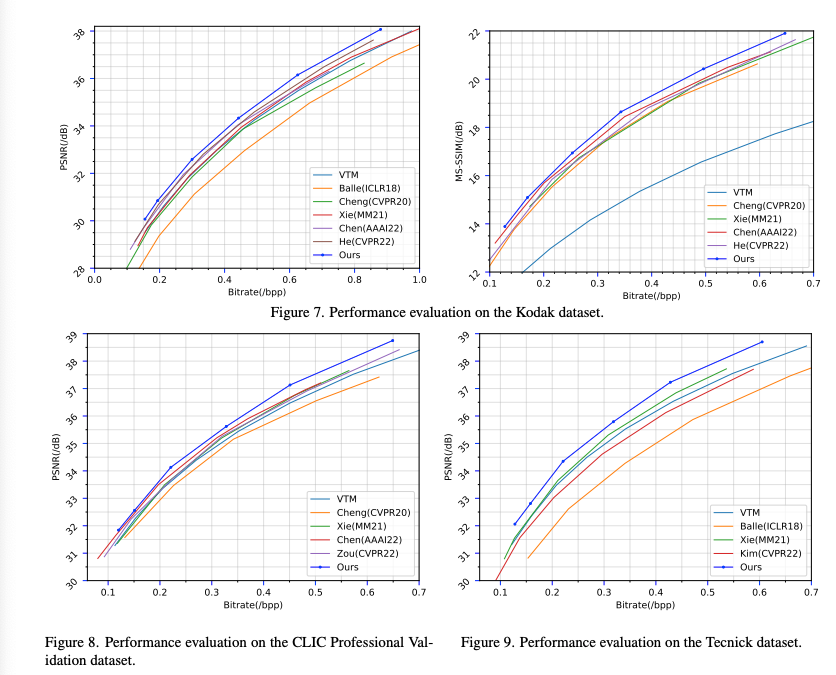
Rate-Distortion Performance에서 PSNR, MS-SSIM 두 손실함수에서 모두 RD-Curve가 비교 모델보다 높게 형성된 것을 확인할 수 있다.
이전. SOTA 모델보다 PSNR은 0.4dB, MS-SSIM은 0.5dB가 같은 bit-rate 기준에서 증가했다고 한다.
Conclusion
- Transformer + CNN으로 local, global modeling을 효율적으로 가능하게 함.
- channel-wise entropy model을 개선하기 위해 swin-transformer 기반의 어텐션 모듈을 제시.
- Transformer + CNN 혼합 모델이 CNN, Transformer을 단일로 사용했을 때 보다 성능이 좋음.
