논문 제목
D-FINE: Redefine Regression Task in DETRs as Fine-grained Distribution Refinement
URL: https://arxiv.org/abs/2410.13842
Github : https://github.com/Peterande/D-FINE
인용수 : 8회 (25.3.26 기준)

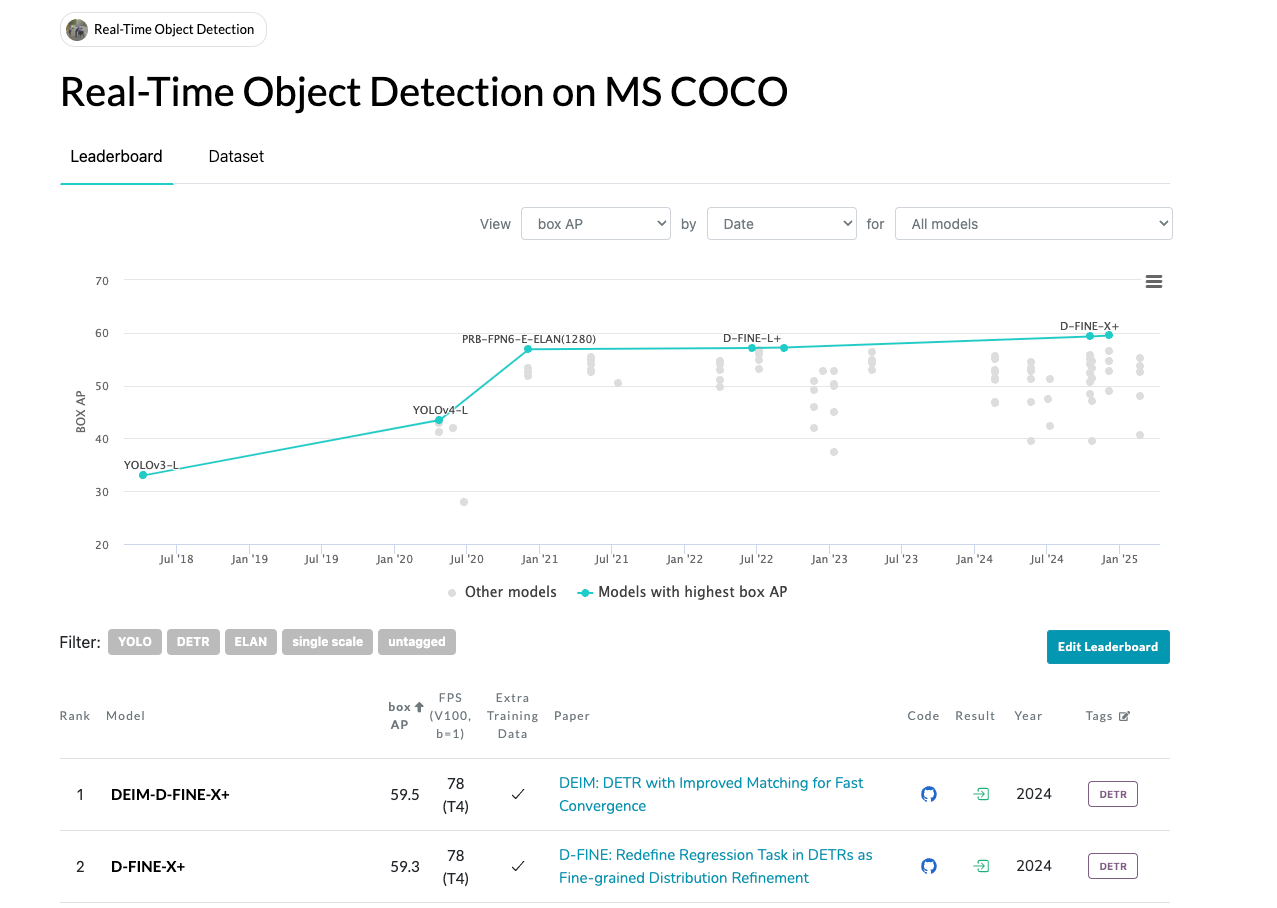
https://paperswithcode.com/sota/real-time-object-detection-on-coco

현재 MS COCO 벤치마크 데이터셋에서 SOTA인 D-FINE 모델에 대해 다뤄보려고 합니다. DETR 계열은 아무래도 YOLO보다는 실시간성에서 밀리는 경향이 있었는데 이제는 YOLO와 견줄정도로 실시간성이 뛰어난 모델들이 나오고 있네요..!

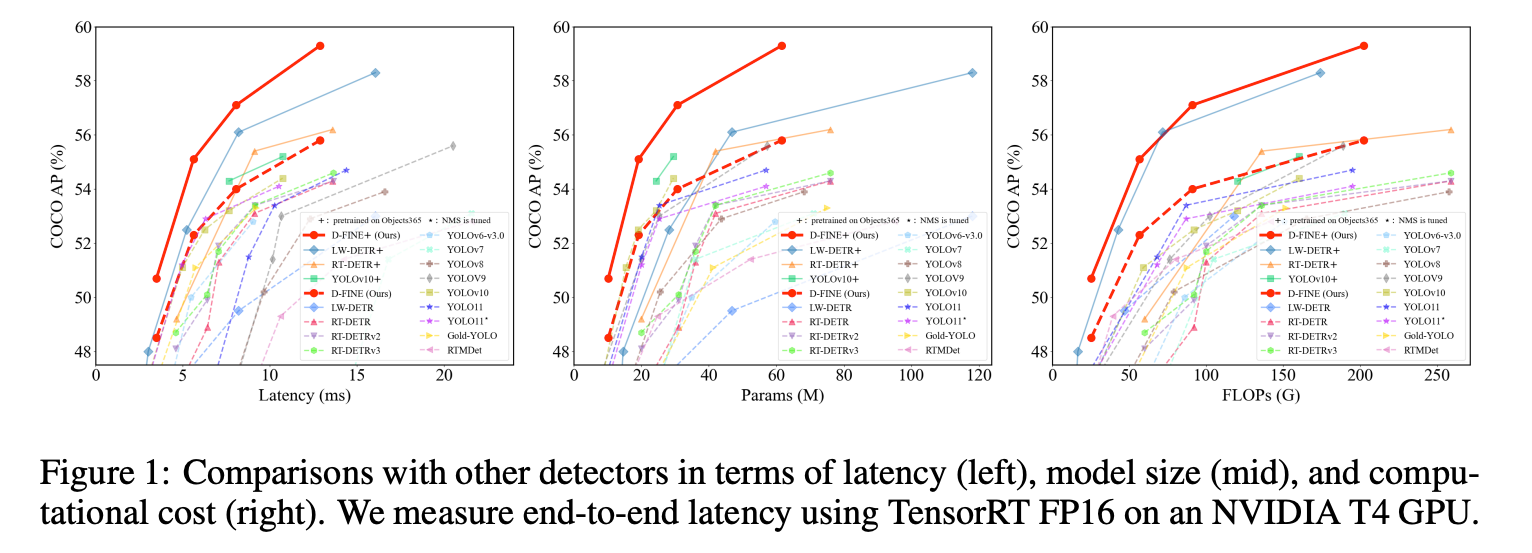
위 이미지를 보시면 YOLOv11과 유사한 수치를 보이고 있습니다. 하지만 COCO AP(%)와 Latency(ms)와는 trade-off 관계가 있어서 YOLOv11보다는 파라미터가 많아 좀 느리긴하지만 준수한 성능을 보입니다.

Abstract

• 본 논문에서는 bounding box regression task를 재정의함으로써 뛰어난 위치 정밀도를 달성하는 강력한 real-time object detector인 D-FINE을 제안.
• D-FINE은 두 가지 핵심 구성요소로 이루어짐. Fine-grained Distribution Refinement (FDR)과 Global Optimal Localization Self-Distillation (GO-LSD).
• FDR은 regression process을 고정된 좌표 예측에서 확률 분포를 반복적으로 정제하는 방식으로 변환하여 위치정확도를 크게 향상시키는 fine-grained intermediate representation 제공.
• GO-LSD는 정제된 분포로부터의 위치 정보를 shallow layers으로 self-distillation를 통해 전달하는 양방향 최적화 전략이며, deeper layers에 대한 residual prediction tasks를 단순화하는 역할.
• D-FINE은 computationally intensive modules 및 연산에서 lightweight optimization을 도입하여 속도와 정확도 간의 더 나은 균형을 달성함.

Introduction

실시간 객체 탐지에서는 YOLO 시리즈가 대표적인 효율적인 Detector로 활약하고 있고, DETR 계열 모델은 global context modeling을 활용하는 강점을 가지지만 높은 지연 시간과 연산 비용이 단점이다. 이를 해결하기 위해 실시간 DETR 변형 모델들이 제안되고 있다.

하지만 DETR은 두 가지 주요 문제가 존재함.
1. 바운딩 박스 회귀에서 고정 좌표 방식은 localization uncertainty을 반영하지 못하며 최적화에 어려움을 준다.
2. 전통적인 지식 증류 방식은 탐지 작업에 비효율적이며, 훈련 비용이 높고 anchor-free 모델과의 시너지가 좋지 않은 문제가 있다.

Related Work

Real-Time / End-to-End Object Detectors

YOLO 시리즈는 아키텍처, 데이터 증강, 훈련 기법에 대한 지속적인 혁신을 통해 실시간 객체 탐지 분야를 이끌었음. 효율적이긴 하지만 YOLO는 일반적으로 Non-Maximum Suppression(NMS)에 의존하며, 이는 속도와 정확도 간의 불안정성을 야기하고 latency을 증가시킴.
DETR은 NMS와 anchor 같은 수작업 구성 요소의 필요성을 제거함으로써 객체 탐지의 패러다임을 제시ㅎ뛰어난 성능을 달성하였지만, 높은 계산 비용으로 인해 실시간 응용에는 부적합했음. RT-DETR과 LW-DETR는 DETR을 실시간 Task에 적용할 수 있도록 만들었음.
YOLO 또한 v10에서 NMS를 제거함으로써 YOLO 시리즈 내에서도 end-to-end detection을 향한 중요한 전환점을 형성.

Distribution-Based Object Detection

기존의 bounding box regression 방식들은 Dirac delta distributions에 의존하여 바운딩 박스 에지를 고정되고 정확한 값으로 간주함. 이러한 방식은 localization uncertainty를 모델링하는 데 어려움이 있다. 이를 해결하기 위해 최근의 모델들은 Gaussian 또는 Discrete 확률 분포를 사용하여 바운딩 박스를 표현하고 있으나, anchor-based framework에 의존해서 YOLOX 또는 DETR과 같은 anchor-free detector와 호환성이 떨어짐.
또한, distribution representation은 coarse-grained 방식으로 설계되며, 효과적인 refinement가 부족하여 보다 정확한 예측을 달성하는 데 어려움이 있음.

Knowledge Distillation

지식 증류(KD)는 강력한 모델 압축 기법이며, 주로 Logit Mimicking을 통해 지식을 전달한다.
DETR를 위한 대부분의 KD 방식은 logit뿐만 아니라 다양한 intermediate representation을 혼합한 hybrid distillation를 주로 사용함.
최근에는 Localization Distillation (LD)가 탐지 작업에 있어 위치 정보를 전달하는 것이 더 효과적임을 보였음.
Self-distillation은 KD의 한 형태로, 모델이 자신의 정제된 출력으로부터 초기 계층이 학습하게 하며, 별도의 teacher 모델 학습이 필요 없어 추가 훈련 비용이 매우 적다는 특징이 있음.

Preliminaries

Bounding box regression

객체 탐지에서의 바운딩 박스 회귀는 전통적으로 Dirac delta distributions를 모델링하는 방식에 의존해왔음.
이 방식은 centroid-based {x,y,w,h} 또는 edge-distance {c,d} 형태로 구성되며 여기서 거리 d ={t,b,l,r}는 앵커 포인트 $c= \{{x_c,y_c}\}$로 부터의 거리로 측정됨.

그러나 바운딩 박스의 에지를 고정되고 정확한 값으로 간주하는 Dirac delta assumption은 특히 애매한 상황에서 localization uncertainty을 모델링하기 어렵게 만든다.

이러한 문제를 해결하기 위해, GFocal은 앵커 포인트로부터 네 개의 에지까지의 거리를 이산화된 확률 분포로 회귀하여 바운딩 박스를 보다 유연하게 모델링함. 바운딩 박스 거리 d ={t,b,l,r}은 다음과 같이 모델링됨.

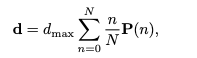
여기서 $d_{max}$는 앵커 중심으로부터 최대거리의 한계를 지정하는 스칼라 값이며, $P(n)$은 네 개의 에지 각각에 대해 후보거리 n의 확률을 나타낸다.

GFocal은 확률 분포를 통해 모호성과 불확실성을 처리하는 데 진전을 이뤘지만, 그 회귀 접근법에는 다음과 같은 구체적인 한계가 여전히 존재함.

1. Anchor Dependency : Regression이 앵커 박스 중심에 묶여 있어 예측 다양성 및 anchor-free frameworks와의 호환성이 제한.
2. No Iterative Refinement : 예측이 one-shot 방식으로 이뤄져서 iterative refinement가 없어서 회귀의 robustness가 떨어짐.
3. Coarse Localization : 고정된 거리 범위와 균등한 bin 간격은 작은 간격의 경우 각 bin이 너무 넓은 값을 대표하게 되어 coarse localization이 발생.

Localization Distillation (LD)

Localization Distillation(LD)는 유망한 접근법으로 탐지 태스크에 있어 위치 정보를 전달하는 것이 보다 효과적임을 보여줬음. LD는 단순히 분류 logit이나 feature map을 모방하는 대신, 교사 모델로부터 유용한 위치 정보를 증류함으로써 학생 모델을 향상시킨다. 하지만 이 방식 역시 앵커 기반 아키텍처에 의존하고, 추가적인 훈련 비용을 초래하는 단점이 존재함.

Method

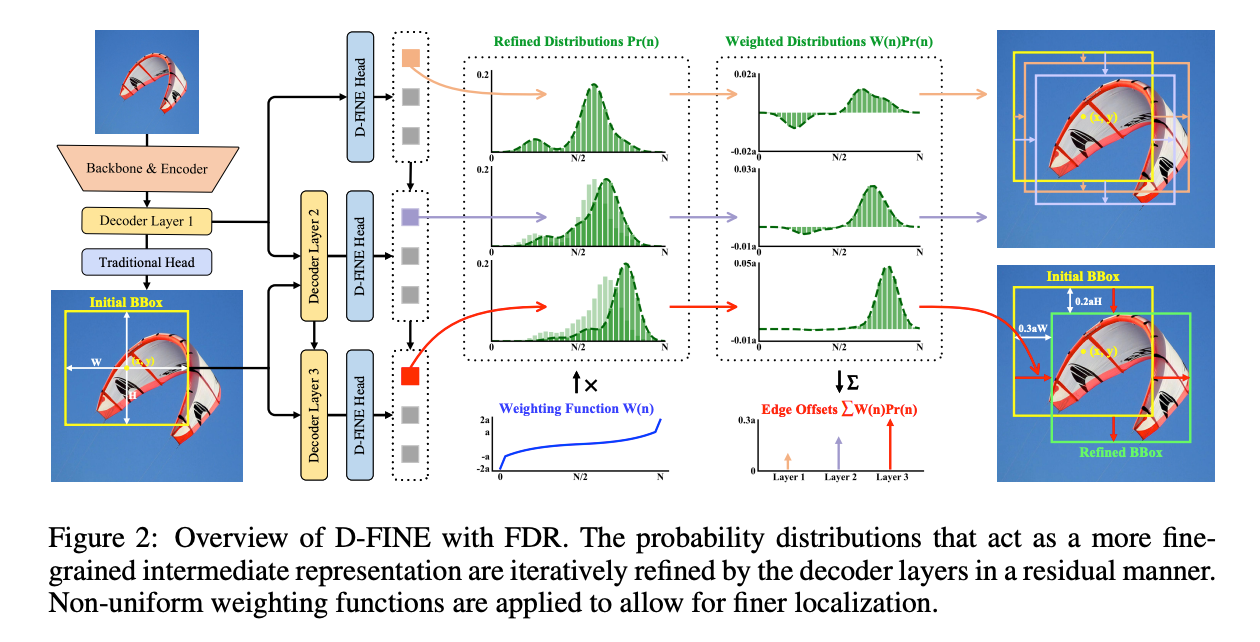
D-FINE은 FDR과 GO-LSD을 통해 추가 파라미터나 훈련 시간의 증가 없이 성능을 크게 향상시켰음.
FDR은 바운딩 박스 예측에 대한 보정을 제공하는 확률 분포를 반복적으로 최적화하며, 보다 정교한 중간 표현을 제공한다. 이 접근은 각 에지의 불확실성을 독립적으로 포착하고 최적화할 수 있음.
FDR은 non-uniform weighting 함수를 활용하여 각 디코더 층에서 보다 정밀하고 점진적인 조정을 가능하게 하며, 이는 위치 정확도를 향상시키고 예측 오류를 줄인다. 그리고 anchor-free,end-toend framework에 호환되어서 보다 유연하고 견고한 최적화 가능.

GO-LSD는 정제된 분포로부터 얻은 위치 정보를 초기 층에 증류함. 훈련이 진행됨에 따라 최종 계층은 점점 더 정밀한 소프트 레이블을 산출하게 된다. 초기 계층은 이 소프트 레이블에 맞춰 자신의 예측을 정렬하게 되어서 보다 정확한 예측을 하게 됨. 초기 예측의 정확도가 향상됨에 따라 이후 계층은 더 작은 잔차를 정제하는 데 집중. 이러한 mutual reinforcement은 시너지 효과를 만들어서 점진적으로 정밀한 위치 예측 가능하게함.

Fine-Grained Distribution Refinement

FDR은 디코더 계층에서 생성된 정교한 분포를 반복적으로 최적화함.
초기에, 첫 번째 디코더 계층은 전통적인 바운딩 박스 회귀 헤드와 D-FINE 헤드를 통해 이진 바운딩 박스와 예비 확률 분포를 예측한다 (두 헤드는 모두 MLP이며, 출력 차원만 다르다). 각 바운딩 박스는 각 에지마다 하나씩, 총 네 개의 분포와 연관되어 있다. 초기 바운딩 박스는 reference boxes로 사용되며 이후의 계층들은 분포를 residual manner로 조정하면서 정제함. 정제된 분포는 각 반복마다 초기 바운딩 박스의 네 에지를 조정하는 데 사용되며 반복할수록 정확도가 점진적으로 향상됨.

초기 바운딩 박스 예측을

라고한다면 여기서 {x,y}는 바운딩 박스의 예측 중심 {W,H}는 너비와 높이를 의미함.

$b^0$를 중심좌표 $c^0=\{x,y\}$와 중심으로부터의 에지 거리 $d^0=\{t,b,l,r\}$로 변환할 수 있다. 여기서 t,b,l,r은 위쪽, 아래쪽, 왼쪽 , 오른쪽 에지까지의 거리를 나타냄.

l번째 계층에서 정제된 에지 거리 $d^l=\{t^l,b^l,l^l,r^l\}$은 다음과 같이 계산됨.

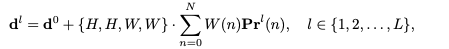
여기서 $Pr^l(n)$은 네 개의 에지 각각에 대한 분리된 확률 분포를 나타냄. 각 분포는 해당 에지의 후보 오프셋 값에 대한 확률을 예측한다.
이 후보들은 가중치 함수 $W(n)$을 통해 결정되며 n은 크기 N의 bin을 인덱싱하며 각 bin은 잠재적인 에지 오프셋 값을 나타냄.
분포들의 가중합은 에지 오프셋을 생성. 이 에지 오프셋들은 이후 초기 바운딩 박스의 높이 H와 너비 W로 스케일링되어서 조정된 값들이 박스크기에 비례할 수 있도록 보장함.

정제된 분포들은 잔차 조정(residual adjustments)을 사용하여 갱신되며 아래와 같다.

여기서 이전 계층의 로짓은 각 bin의 오프셋 값에 대한 confidence를 반영함. 현재 계층은 잔차 로짓($\Delta$~)을 예측하며 이전 로짓에 더해져서 새로운 로짓을 형성함. 갱신된 로짓들을 softmax함수로 정규화되어 정제된 확률 분포를 출력함.

정밀하고 유연한 조정을 가능하게 하기 위해, 가중치 함수는 다음과 같이 정의됨.

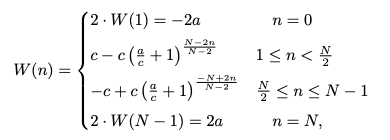
여기서 a와 c는 상한값 및 함수의 curvature를 제어하는 하이퍼파라미터임. W(n)의 형태는 바운딩 박스 예측이 부정확할 때 작은 curvature로 미세 조정을 가능하게함.
반대로 바운딩 박스 예측이 매우 부정확한 경우 에지 근처에서 더 큰 curvature와 경계에서의 급격한 변화는 W(n)이 큰 보정을 수행할 수 있는 충분한 유연성을 제공하도록 보장함.

우리의 분포 예측 정확도를 향상시키고, ground truth 값과의 정렬을 유도하기 위해,
Distribution Focal Loss (DFL)에서 영감 받아 Fine-Grained Localization (FGL) Loss를 제안함. 손실함수 수식은 아래와 같다.

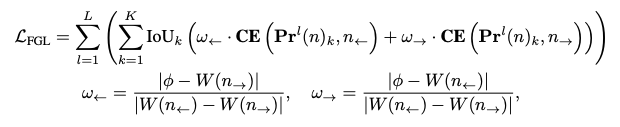
여기서 $Pr^l()$은 k번째 예측에 대한 확률분포를 나타냄. ϕ는 relative offset으로 아래와 같이 계산됨.

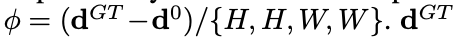
interpolation (오메가)은 GT 위치와 정확히 정렬된 분포 학습을 가능하게 함.
IoU 기반 가중치를 도입함으로써, FGL 손실은 예측 분포가 ground truth 주변에 집중되도록 유도하며 보다 정밀하고 신뢰도 높은 바운딩 박스 회귀를 가능하게 함.

Global Optimal Localization Self-Distillation

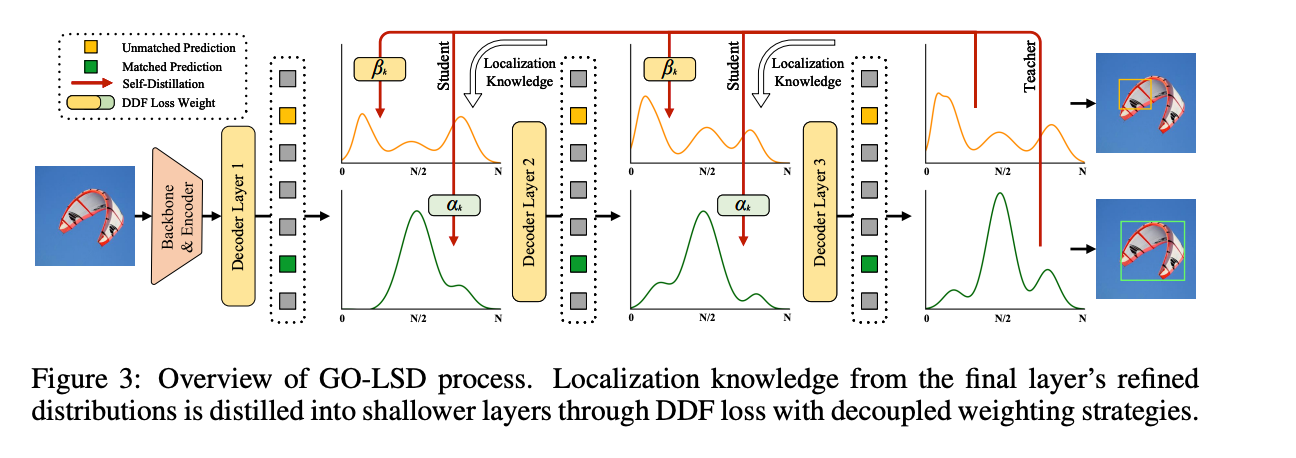
GO-LSD는 디코더의 최종 계층이 정제한 분포 예측을, 초기 계층에 위치 localization knowledge으로 전달하는 데 활용된다.
위 그림처럼 각 계층의 예측에 Hungarian Matching을 적용하여 수행되며 모델의 각 계층에서 바운딩 박스 매칭을 식별하여 전체 계층에 걸쳐 단일한 union set을 생성한다. 이 union set을 사용하면 가장 정확한 후보 예측을 다양한 계층에서 모두 공유할 수 있어서 증류 효과를 전체적으로 누릴 수 있게 된다.

이러한 글로벌 매칭을 정제하는 것 외에도, GO-LSD는 training 도중 매칭되지 않은 예측들까지 포함시켜 전체적인 안정성을 향상시키고 결과적으로 성능 개선으로 이어진다.

비록 localization은 예측을 통해 이루어지지만 classification 작업은 여전히 1:1 매칭 원칙을 따른다. 이러한 strict matching 은 union set에 포함된 일부 예측들이 정확하게 위치는 되었지만confidence score는 낮다는 것을 의미한다. 이러한 confidence가 낮은 예측들은 종종 정확한 위치 정보를 갖는 후보를 나타내며 여전히 효과적으로 증류될 필요가 있다.

이 문제를 해결하기 위해 본 논문에서는 Decoupled Distillation Focal (DDF) Loss를 제안했다.
이 손실 함수는 decoupled 가중치 전략을 적용하여 IoU는 높지만 confidence가 낮은 예측에 적절한 가중치를 부여할 수 있도록 설계되었다.
DDF Loss는 매칭된 예측 과 매칭되지 않은 예측의 개수에 따라 기여도와 개별 손실을 균형 있게 조정한다. 이러한 접근법은 더 안정적이고 효과적인 자기 증류를 가능하게 한다고함.
Decoupled Distillation Focal Loss는 아래와 같이 정의된다.

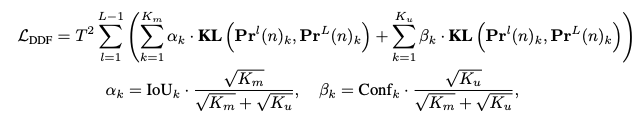
여기서 KL은 Kullback-Leibler divergence이며 T는 로짓의 smoothing을 조절하는 파라미터이다.

Experiments

Experiment Setup

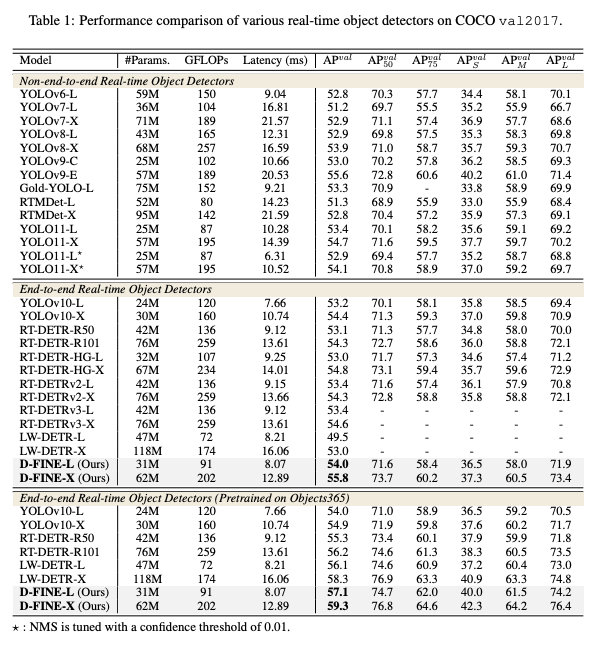
제안한 방법의 효과를 검증하기 위해 COCO 및 Objects365 데이터셋에서 실험을 수행하였음.
D-FINE은 COCO의 표준 평가 지표를 사용해 평가되며, 여기에는 IoU 임계값 0.50부터 0.95까지를 평균한 평균 정밀도(AP),특정 임계값에서의 AP (AP₅₀ 및 AP₇₅), 그리고 객체 크기별 AP (작은 객체: AP_S, 중간 크기: AP_M, 큰 객체: AP_L)가 포함된다.

Comparison with Real-Time Detectors

• D-FINE은 COCO 벤치마크에서 다양한 실시간 객체 탐지기(YOLO 시리즈, RT-DETR 등) 와 성능 및 속도를 비교함.
• 정확도(AP) 면에서 D-FINE은 대부분의 기존 모델보다 우수한 성능을 기록.

Effectiveness on Various DETR Models

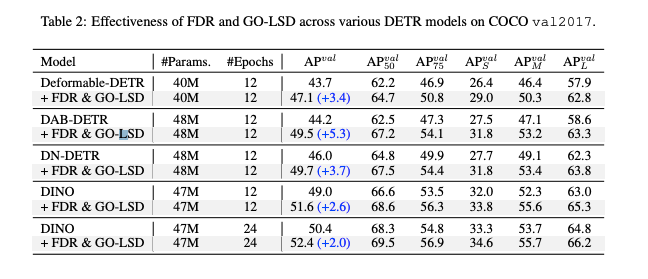
• 제안한 D-FINE의 핵심 구성요소인 FDR (Fine-grained Distribution Refinement) 과 GO-LSD (Global Optimal Localization Self-Distillation) 를 다양한 DETR 계열 탐지기들(예: Deformable-DETR, DAB-DETR, DN-DETR 등)에 적용해봄.
• 실험 결과, D-FINE 구성요소를 기존 DETR 아키텍처에 추가하면 모두 성능 향상을 보임

Visualization Analysis

D-FINE은 다음과 같은 강점을 보여줌

• 더 정밀한 바운딩 박스 위치
• 더 정확한 box 크기 및 형태 정렬

예측 분포 시각화에서도 D-FINE은 분포가 더 concentrated 되어 있으며 에지 위치에 대한 불확실성이 낮게 나타남. 이는 이는 FDR이 반복적으로 위치 분포를 정제하고, GO-LSD가 얕은 계층까지 정제된 정보를 전달해주기 때문임.

Conclusion

D-FINE은 Fine-grained Distribution Refinement (FDR) 와 Global Optimal Localization Self-Distillation (GO-LSD) 를 통해 DETR 모델에서의 바운딩 박스 회귀 과제를 재정의하는, 강력한 실시간 객체 탐지기임.
COCO 데이터셋에 대한 실험 결과는 D-FINE이 최첨단(state-of-the-art)의 정확도와 효율성을 달성하며 모든 기존 실시간 탐지기를 능가함을 보여줬음.

하지만 경량화된 D-FINE 모델과 다른 소형 모델들 간의 성능 격차는 여전히 존재하여서 한계점 및 향후 연구 방향을 시사함.