1. Introduction
이번엔 <Titanic Top 4% with ensemble modeling>이란 제목의 Kaggle 노트북에 대해 공부해보자. 이 노트북은 Yassine Ghouzam이 작성한 노트북으로 처음 kaggle에 작성한 노트북이라 한다.(부럽..)
이 노트북은 크게 세 개의 과정을 거친다.
- 피처 분석(Feature analysis)
- 피처 엔지니어링(Feature engineering)
- 모델링(Modeling)
Titanic 데이터는 아래와 같이 구성되어 있다.
- PassengerId: 탑승자 데이터 일련번호
- Survived: 생존여부, 0 = 사망, 1 = 생존
- Pclass: 티켓의 선실 등급, 1 = 일등석, 2 = 이등석, 3 = 삼등석
- Sex: 탑승자 성별
- Name: 탑승자 이름
- Age: 탑승자 나이
- SibSp: 같이 탑승한 형제, 자매 또는 배우자 인원 수
- Parch: 같이 탑승한 부모님 또는 자녀 인원 수
- Ticket: 티켓 번호
- Fare: 요금
- Cabin: 선실 번호
- Embarked: 탑승 항구, C = Cherbourg, Q = Queenstown, S = Southampton
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from collections import Counter
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier, ExtraTreesClassifier, VotingClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, learning_curve
import warnings
warnings.filterwarnings('ignore')
sns.set(style='white', context='notebook', palette='deep')sns.set(style='white', context='notebook', palette='deep')
- style: 배경색
- context: 그래프의 배율 조정으로, {paper, notebook, talk, poster}중에 설정 할 수 있다.
- palette: 어떤 색상 모음을 사용할지 선택하며, {deep, muted, pastel, bright, dark, colorblind}를 기본 팔레트로 제공한다.
2. Load and Check Data
2.1 Load Data
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
IDtest = test['PassengerId']2.2 Outlier Detection
여기서 사회조사분석사를 공부하면서 배웠던 개념인 이상치(Outlier)에 대해 나온다. 먼저 사분위수는 데이터 표본을 4개의 동일한 부분(25%, 50%, 75%)으로 나눈 값이고, 그 중 제 1 사분위수(Q1, 데이터 25%가 이 값보다 작거나 같음), 제 3 사분위수(Q3, 데이터 75%가 이 값보다 작거나 같음)로 IQR(Q3 - Q1)을 구한다. 이때 우리는 Q1 - 1.5 * IQR 보다 작거나 Q3 + 1.5 * IQR 보다 큰 값을 이상치라고 한다.
필자는 Tukey의 범위 검정 개념을 이용해서 Age, SibSp, Parch, Fare에 대한 이상치 분석을 통해 3개이상의 이상치를 가진 사람들을 알아본다.
from collections import Counter는 컨테이너에 동일한 값의 자료가 몇 개인지를 파악하는데 사용하는 객체로 collections.Counter()의 결과값은 딕셔너리 형태로 출력된다.
ex) lst = ['aa', 'cc', 'dd', 'aa', 'bb', 'ee']의 요소 개수를 collections.Counter()를 이용하여 구할 수 있다.
Output: Counter({'aa': 2, 'cc': 1, 'dd': 1, 'bb': 1, 'ee': 1})
features = ['Age', 'SibSp', 'Parch', 'Fare']
def detect_outliers(df, n, features):
outlier_indices = []
for col in features:
Q1 = np.percentile(df[col], 25)
Q3 = np.percentile(df[col], 75)
IQR = Q3 - Q1
outlier_step = 1.5 * IQR
outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
outlier_indices.extend(outlier_list_col)
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
return multiple_outliers
Outliers_to_drop = detect_outliers(train, 2, features)
train.loc[Outliers_to_drop]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.00 | C23 C25 C27 | S |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.00 | C23 C25 C27 | S |
| 159 | 160 | 0 | 3 | Sage, Master. Thomas Henry | male | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 180 | 181 | 0 | 3 | Sage, Miss. Constance Gladys | female | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 201 | 202 | 0 | 3 | Sage, Mr. Frederick | male | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 324 | 325 | 0 | 3 | Sage, Mr. George John Jr | male | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.00 | C23 C25 C27 | S |
| 792 | 793 | 0 | 3 | Sage, Miss. Stella Anna | female | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 846 | 847 | 0 | 3 | Sage, Mr. Douglas Bullen | male | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
| 863 | 864 | 0 | 3 | Sage, Miss. Dorothy Edith "Dolly" | female | NaN | 8 | 2 | CA. 2343 | 69.55 | NaN | S |
3개 이상의 이상치를 갖는 10개의 데이터는 볼 수 있다. 28, 89, 342번 승객은 높은 티켓 가격을, 다른 승객들은 높은 SibSp 값을 가지고 있다. 이 승객들을 제외하자.
reset_index는 인덱스를 리셋시키고 drop=True는 디폴트는 False로, True는 기존 인덱스를 버리고 재배열해준다.
train = train.drop(Outliers_to_drop, axis=0).reset_index(drop=True)2.3 Joining Train and Test Set
concat()은 데이터 속성 형태가 동일한 데이터 세트를 합칠 때 사용한다. axis 가 0이면 위, 아래로 합치고 1이면 좌, 우로 합친다.
train_len = len(train)
dataset = pd.concat(objs=[train, test], axis=0).reset_index(drop=True)2.4 Check for Null and Missing Values
dataset = dataset.fillna(np.nan)
dataset.isnull().sum()PassengerId 0
Survived 418
Pclass 0
Name 0
Sex 0
Age 256
SibSp 0
Parch 0
Ticket 0
Fare 1
Cabin 1007
Embarked 2
dtype: int64Age와 Cabin에 많은 양의 결측값이 있는 것을 알 수 있고, Survived의 결측값은 Test dataset에서 온 것으로 확인된다.(테스트 세트의 Survived열은 비어있어서 NaN으로 대체됨.)
train.info()
train.isnull().sum()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 881 entries, 0 to 880
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 881 non-null int64
1 Survived 881 non-null int64
2 Pclass 881 non-null int64
3 Name 881 non-null object
4 Sex 881 non-null object
5 Age 711 non-null float64
6 SibSp 881 non-null int64
7 Parch 881 non-null int64
8 Ticket 881 non-null object
9 Fare 881 non-null float64
10 Cabin 201 non-null object
11 Embarked 879 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 82.7+ KB
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 170
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 680
Embarked 2
dtype: int64train.head()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
train.dtypesPassengerId int64
Survived int64
Pclass int64
Name object
Sex object
Age float64
SibSp int64
Parch int64
Ticket object
Fare float64
Cabin object
Embarked object
dtype: objecttrain.describe()| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 881.000000 | 881.000000 | 881.000000 | 711.000000 | 881.000000 | 881.000000 | 881.000000 |
| mean | 446.713961 | 0.385925 | 2.307605 | 29.731603 | 0.455165 | 0.363224 | 31.121566 |
| std | 256.617021 | 0.487090 | 0.835055 | 14.547835 | 0.871571 | 0.791839 | 47.996249 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 226.000000 | 0.000000 | 2.000000 | 20.250000 | 0.000000 | 0.000000 | 7.895800 |
| 50% | 448.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.000000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 30.500000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 5.000000 | 6.000000 | 512.329200 |
3. Feature Analysis
3.1 Numerical values
서수형 값들에 대해 상관관계 분석을 진행한다.
annot=True 파라미터는 각 박스 안에 상관계수를 표시하는지를 결정한다.
g = sns.heatmap(train[['Survived', 'SibSp', 'Parch', 'Age', 'Fare']].corr(), annot=True, fmt='.2f', cmap='coolwarm')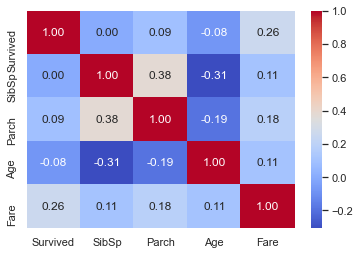
Fare 만이 생존에 대해 상관관계를 가지지만 이것이 다른 피처들이 쓸모없다는 것을 의미하진 않는다. 각 특징들에 대해 분석해 보자.
SibSp
g = sns.factorplot('SibSp', 'Survived', data=train, kind='bar', size=6, palette='muted')
# despine은 y축의 선을 없앨 것인지를 결정한다.
g.despine(left=True)
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedf1ade520>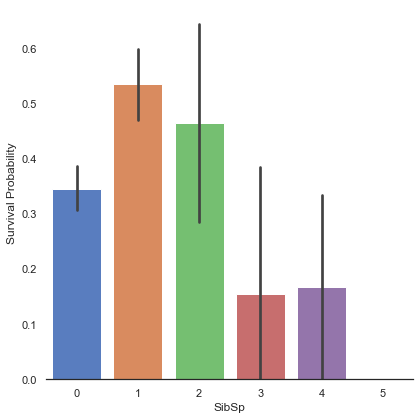
형제/자매의 수가 적은 사람들(1, 2)의 생존률이 더 높은 것으로 관찰된다.
Parch
g = sns.factorplot('Parch', 'Survived', data=train, kind='bar', size=6, palette='muted')
g.despine(left=True)
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedf377be80>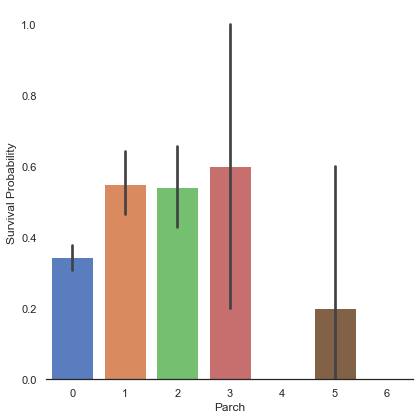
부모/자식의 수가 3인 사람의 생존률이 가장 높게 나타났고, 아예 없거나 5명인 대가족은 생존률이 낮게 나타났다.
Age
sns.FacetGrid를 사용하면 여러 개의 그래프를 그릴 수 있다. 여기선 Survived가 0과 1일때의 히스토그램을 그렸다.
g = sns.FacetGrid(train, col='Survived')
g = g.map(sns.distplot, 'Age')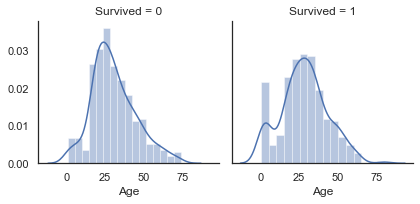
Age의 분포는 가우스 분포(정규분포)의 형태를 띄며, 60-80세의 생존률이 낮고, 어린 승객의 생존률이 높은 것을 알 수 있다.
비록 Age와 Survived는 상관관계가 없지만, 연령별 승객의 생존률 차이가 존재하는 것을 알 수 있다. 좀 더 확실하게 비교하기위해 데이터의 분포를 확인하는 커널밀도추정(Kernel Density Estimater) 그래프를 그려보자.
g = sns.kdeplot(train['Age'][(train['Survived'] == 0) & (train['Age'].notnull())], color='Red', shade=True)
g = sns.kdeplot(train['Age'][(train['Survived'] == 1) & (train['Age'].notnull())], ax=g, color='Blue', shade=True)
g.set_xlabel('Age')
g.set_ylabel('Frequency')
g.legend(['Not Survived', 'Survived'])<matplotlib.legend.Legend at 0x7fedef636820>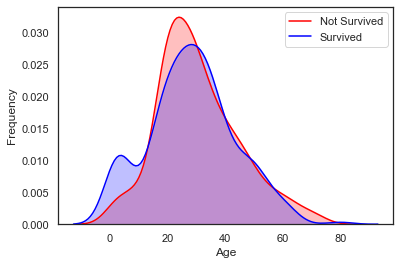
두 밀도 그래프를 겹쳐본 결과 0-5세의 아이들의 생존률이 높게 나타나는 것을 알 수 있다.
Fare
dataset['Fare'].isnull().sum()1코드 실행 결과 Fare의 결측값은 1개이므로 그 값은 중간값으로 대체
dataset['Fare'] = dataset['Fare'].fillna(dataset['Fare'].median())skew()는 비대칭도(왜도)인 skewness를 뜻한다.
일반적으로 왜도는 첨도와 같이 얘기하는데 첨도는 뾰족한 정도, 왜도는 비대칭 정도를 의미한다.
왜도의 기준은 0, 첨도의 기준은 3으로 정규분포와 비교한다.
- 왜도가 0보다 크면 오른쪽으로 긴 꼬리를 갖는다.
- 왜도가 0보다 작으면 왼쪽으로 긴 꼬리를 갖는다.
- 첨도가 3보다 크면 peak점이 뾰족하다.
- 첨도가 3보다 작으면 peak점이 덜 뾰족하다.
g = sns.distplot(dataset['Fare'], color='m', label='Skewness : %.2f'%(dataset['Fare'].skew()))
g.legend(loc='best')<matplotlib.legend.Legend at 0x7fedf1eb98e0>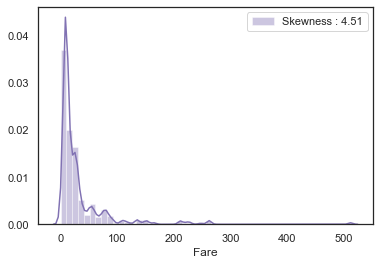
Fare의 분포가 매우 비대칭인 것을 알 수 있는데, 만약 이대로 모델에 넣어준다면 모델이 몇 개 없는 outlier에 민감하게 반응하면, 잘못 학습할 수도 있다. 그래서 Fare에 log 를 취한 후 다시 확인해보도록 하자.
dataset['Fare'] = dataset['Fare'].map(lambda i: np.log(i) if i > 0 else 0)g = sns.distplot(dataset['Fare'], color='m', label='Skewness : %.2f'%(dataset['Fare'].skew()))
g.legend(loc='best')<matplotlib.legend.Legend at 0x7fedf1466f10>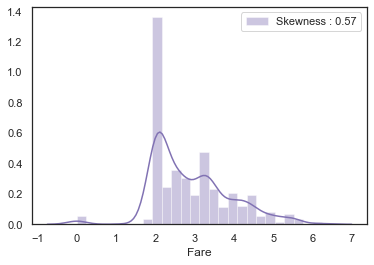
왜도의 값이 4.51 에서 0.57 로 눈에 띄게 줄어든 것을 알 수 있다.
3.2 Categorical Values
Sex
위에서 서수형 데이터들을 보았으니 이번엔 카테고리형 데이터들에 대해 알아보자.
g = sns.barplot('Sex', 'Survived', data=train)
g.set_ylabel('Survival Probability')Text(0, 0.5, 'Survival Probability')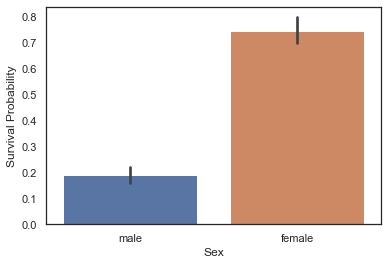
train[['Sex', 'Survived']].groupby('Sex').mean()| Survived | |
|---|---|
| Sex | |
| female | 0.747573 |
| male | 0.190559 |
남성의 생존률보다 여성의 생존률이 확연하게 높은 것을 알 수 있다. Sex는 생존 예측의 중요한 피처가 될 것이라고 생각할 수 있다.
Pclass
g = sns.factorplot('Pclass', 'Survived', data=train, kind='bar', size=6, palette='muted')
g.despine(left=True)
g.set_ylabels('Survivial Probability')<seaborn.axisgrid.FacetGrid at 0x7fedef2c32b0>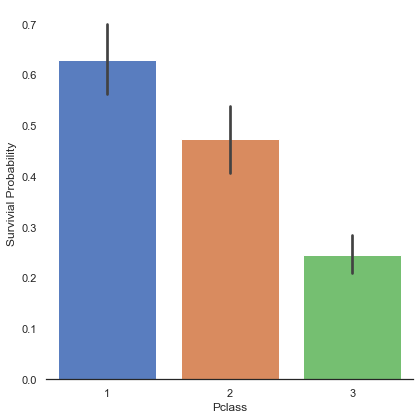
Pclass가 낮을수록, 즉 좋은 일등석에 가까울수록 생존률이 높아지는 것을 알 수 있다. 이번엔 성별별, 각 클래스별 생존률을 알아보자.
g = sns.factorplot('Pclass', 'Survived', hue='Sex', data=train, kind='bar', size=6, palette='muted')
g.despine(left=True)
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedefdda820>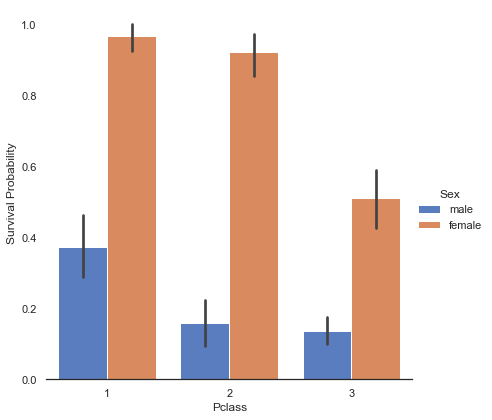
남성, 여성에 상관없이 1등석과 2등석의 생존률이 3등석에 비해 높다는 것을 알 수 있다.
Embarked
dataset['Embarked'].isnull().sum()2Embarked의 Null 값이 2개밖에 없고 대부분 Southampton 에서 탑승했으므로 Null 값을 "S"로 대체한다.
dataset['Embarked'] = dataset['Embarked'].fillna('S')g = sns.factorplot('Embarked', 'Survived', data=train, size=6, kind='bar', palette='muted')
g.despine(left=True)
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedd589cd30>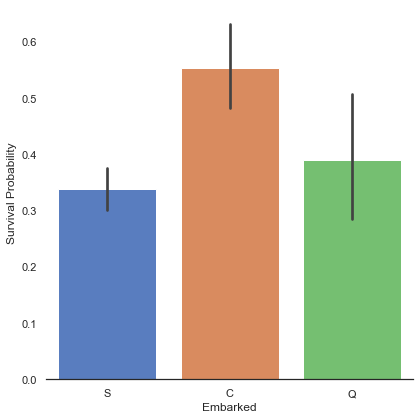
Cherbourg(C)에서 탑승한 승객의 생존률이 높게 나타났다. 필자는 여기서 C에서 탑승한 승객의 생존률이 높은 이유를 1등석 승객이 많아서 일것으로 가정하고 아래 비교 그래프를 그린다.
g = sns.factorplot('Pclass', col='Embarked', data=train, size=6, kind='count', palette='muted')
g.despine(left=True)
g.set_ylabels('Count')<seaborn.axisgrid.FacetGrid at 0x7fedf3474e80>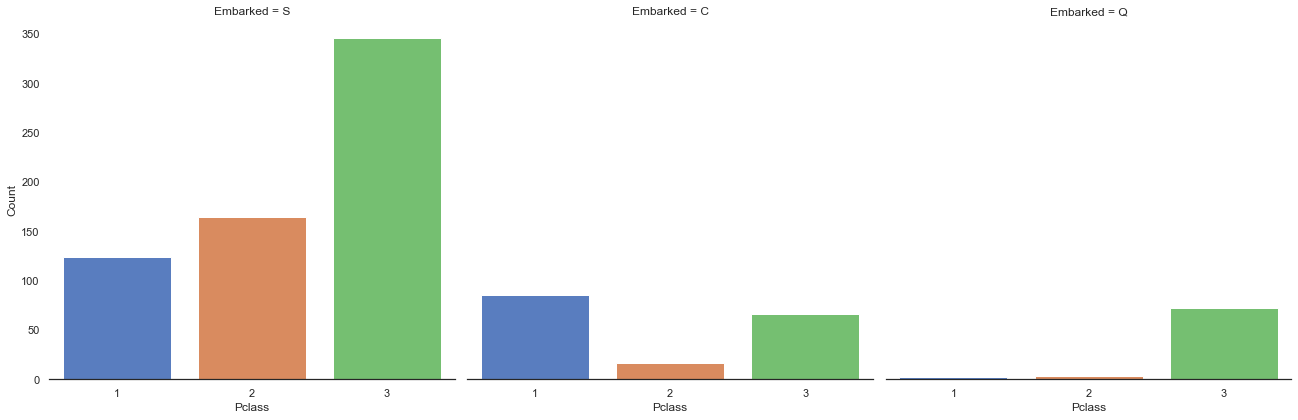
Southampton(S)와 Queenstown(Q)에서 탑승한 승객들은 대부분 3등석 승객이지만, Cherbourg(C)에서 탑승한 승객은 1등석 승객이 더 많았다.
4. Filling Missing Values
4.1 Age
위에서 Age에는 256개의 Null 데이터가 존재하는 것을 확인하였다. 존재하는 Null 값들을 채우기위해 Sex, Parch, Pclass, SibSp 중 어떤 변수가 가장 상관관계가 있는지 확인해보자.
sns.factorplot('Sex', 'Age', data=dataset, kind='box')
sns.factorplot('Sex', 'Age', hue='Pclass', data=dataset, kind='box')
sns.factorplot('Parch', 'Age', data=dataset, kind='box')
sns.factorplot('SibSp', 'Age', data=dataset, kind='box')<seaborn.axisgrid.FacetGrid at 0x7fedf3956df0>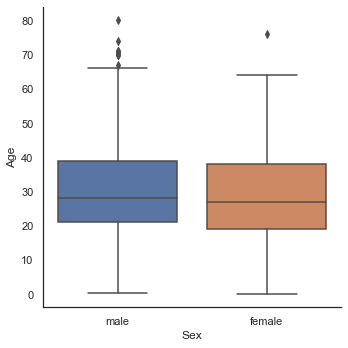
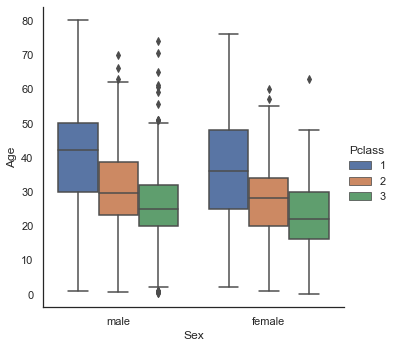
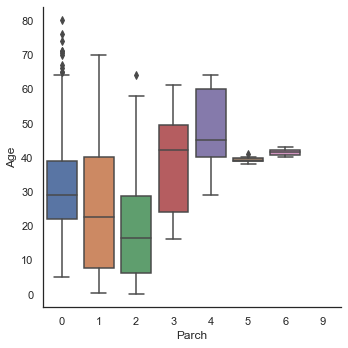
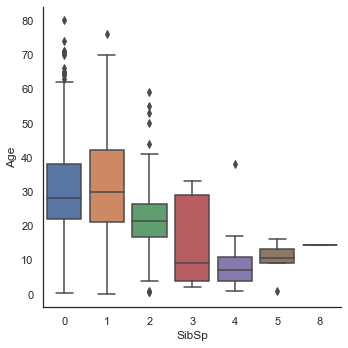
- Sex는 남, 녀 모두에서 비슷한 양상을 보여 Age를 예측하기 중요한 정보는 아니라고 판단된다.
- 1등급 승객이 2등급 승객보다 나이가 많고, 2등급 승객이 3등급 승객보다 나이가 많은 것으로 나타난다.
- 부모/자식을 많이 가진 승객일수록 나이가 많다.
- 형제/자매를 많이 가진 승객일수록 나이가 어리다.
성별이 문자형 데이터이므로 숫자형으로 변환하고 상관관계 분석을 해보자.
dataset['Sex'] = dataset['Sex'].map({"male": 0, "female": 1})
sns.heatmap(dataset[['Age', 'Sex', 'SibSp', 'Parch', 'Pclass']].corr(), cmap='BrBG', annot=True)<matplotlib.axes._subplots.AxesSubplot at 0x7fedf30df7c0>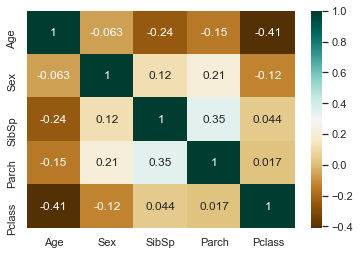
상관관계 분석에 따르면 Age는 Sex 와 상관관계가 없고, SibSp, Parch, Pclass 와 부정적 상관관계를 갖는다. 위에서 부모/자식을 많이 가진 승객일수록 나이가 많다고 나타났는데 일반적인 상관관계는 부정적이다.
상관관계가 있다고 나온 SibSp, Parch, Pclass 를 이용해서 Age의 Null 값을 채우자.
index_NaN_age = list(dataset['Age'][dataset['Age'].isnull()].index)
for i in index_NaN_age:
age_med = dataset['Age'].median()
age_pred = dataset['Age'][((dataset['SibSp'] == dataset.iloc[i]['SibSp']) & (dataset['Parch'] == dataset.iloc[i]['Parch']) & (dataset['Pclass'] == dataset.iloc[i]['Pclass']))].median()
if np.isnan(age_pred):
dataset['Age'].iloc[i] = age_med
else:
dataset['Age'].iloc[i] = age_predsns.factorplot('Survived', 'Age', data=train, kind='box')
sns.factorplot('Survived', 'Age', data=train, kind='violin')<seaborn.axisgrid.FacetGrid at 0x7fedd869c160>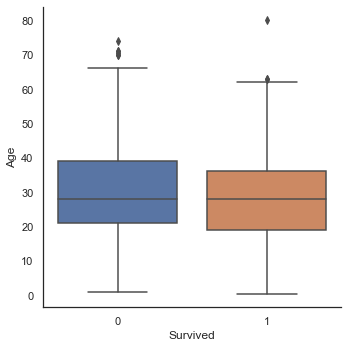
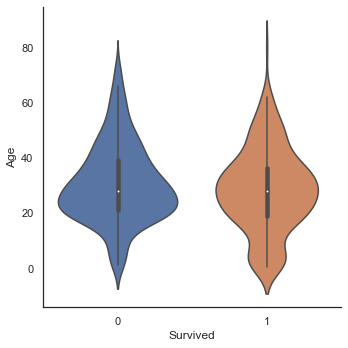
생존하지 못한 승객과 생존한 승객의 연령의 중간값은 거의 차이가 없다. 하지만 violin 그래프에서 여전히 아이들의 생존률은 높은 것으로 나타났다.
5. Feature Engineering
5.1 Name/Title
dataset['Name'].head()0 Braund, Mr. Owen Harris
1 Cumings, Mrs. John Bradley (Florence Briggs Th...
2 Heikkinen, Miss. Laina
3 Futrelle, Mrs. Jacques Heath (Lily May Peel)
4 Allen, Mr. William Henry
Name: Name, dtype: object이름은 Mr, Mrs, Miss 등의 정보를 담고있고, 이 정보를 추출해내어서 모델에 추가해보는 것도 가능할 것 같다.
dataset_title = [i.split(',')[1].split('.')[0].strip() for i in dataset['Name']]
dataset['Title'] = pd.Series(dataset_title)
dataset['Title'].head()0 Mr
1 Mrs
2 Miss
3 Mrs
4 Mr
Name: Title, dtype: objectg = sns.countplot('Title', data=dataset)
g = plt.setp(g.get_xticklabels(), rotation=45)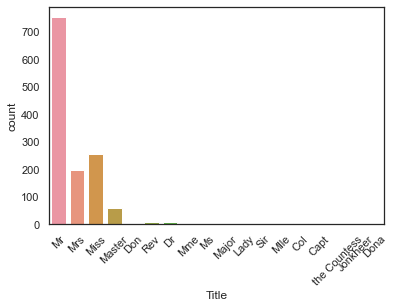
17개의 Title 이 나왔는데 이것들을 4가지 카테고리(Master, Miss~Mrs, Mr, Rare)로 바꿀 수 있다.
dataset["Title"] = dataset["Title"].replace(['Lady', 'the Countess','Countess','Capt', 'Col','Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset["Title"] = dataset["Title"].map({"Master":0, "Miss":1, "Ms" : 1 , "Mme":1, "Mlle":1, "Mrs":1, "Mr":2, "Rare":3})
dataset["Title"] = dataset["Title"].astype(int)g = sns.countplot(dataset['Title'])
g = g.set_xticklabels(['Master', 'Miss~Mrs', 'Mr', 'Rare'])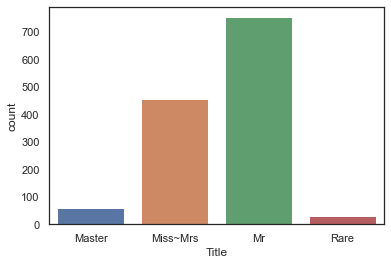
g = sns.factorplot('Title', 'Survived', data=dataset, kind='bar')
g = g.set_xticklabels(['Master', 'Miss~Mrs', 'Mr', 'Rare'])
g = g.set_ylabels('Survival Probability')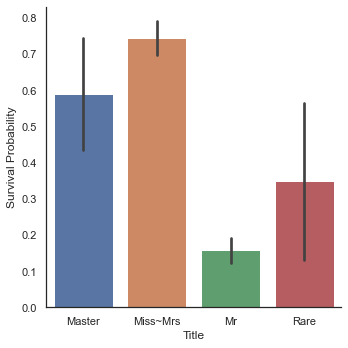
여성의 생존률이 역시 가장 높으며 Rare로 분류한 승객들의 생존률도 꽤나 높은 것을 볼 수 있다. 이제 이름은 필요없으니 삭제한다.
dataset.drop(labels=['Name'], axis=1, inplace=True)5.2 Family Size
필자는 대가족의 경우 대피가 더 힘들 것이라 생각해서 SibSp, Parch, 1(자기자신) 을 합친 Fsize(Family Size) 피처를 만든다.
dataset['Fsize'] = dataset['SibSp'] + dataset['Parch'] + 1g = sns.factorplot('Fsize', 'Survived', data=dataset)
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedd86fd4c0>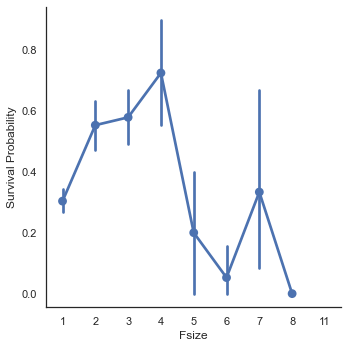
필자의 예상대로 대가족인 경우 생존률이 낮아짐을 알 수 있다. 그리고 여기서 4개의 카테고리로 나누기로 한다.
dataset['Single'] = dataset['Fsize'].map(lambda s: 1 if s == 1 else 0)
dataset['SmallF'] = dataset['Fsize'].map(lambda s: 1 if s == 2 else 0)
dataset['MedF'] = dataset['Fsize'].map(lambda s: 1 if 3 <= s <= 4 else 0)
dataset['LargeF'] = dataset['Fsize'].map(lambda s: 1 if s >= 5 else 0)f, ax = plt.subplots(2, 2, figsize=(18, 8))
sns.barplot('Single', 'Survived', data=dataset, ax=ax[0, 0])
ax[0, 0].set_ylabel('Survival Probability')
sns.barplot('SmallF', 'Survived', data=dataset, ax=ax[0, 1])
ax[0, 1].set_ylabel('Survival Probability')
sns.barplot('MedF', 'Survived', data=dataset, ax=ax[1, 0])
ax[1, 0].set_ylabel('Survival Probability')
sns.barplot('LargeF', 'Survived', data=dataset, ax=ax[1, 1])
ax[1, 1].set_ylabel('Survival Probability')Text(0, 0.5, 'Survival Probability')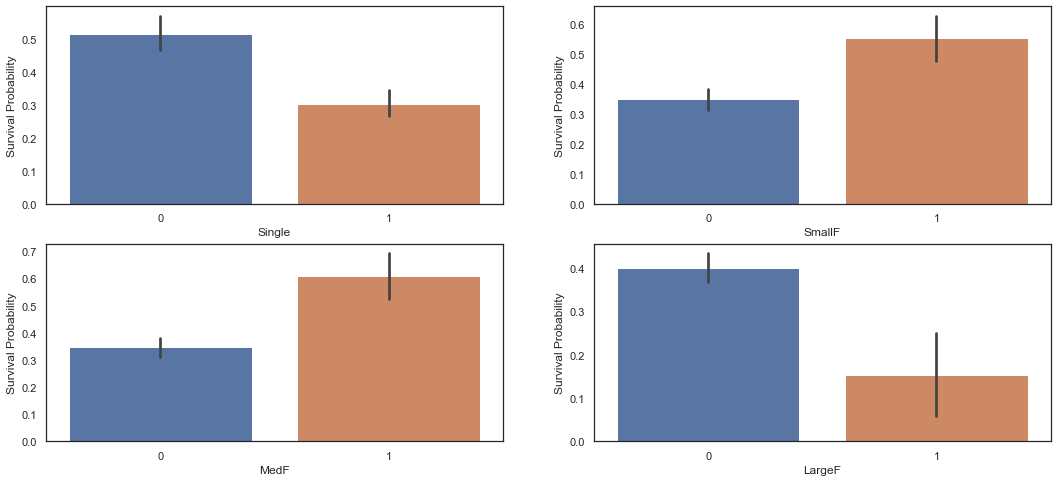
Small, Medium Family 의 생존률이 Single, Large Family 의 생존률보다 높은 것을 알 수 있다.
Title 과 Embarked 에 One-Hot Encoding을 하자
dataset = pd.get_dummies(dataset, columns=['Title'])
dataset = pd.get_dummies(dataset, columns=['Embarked'], prefix='Em')
dataset.head()| PassengerId | Survived | Pclass | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | ... | SmallF | MedF | LargeF | Title_0 | Title_1 | Title_2 | Title_3 | Em_C | Em_Q | Em_S | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.0 | 3 | 0 | 22.0 | 1 | 0 | A/5 21171 | 1.981001 | NaN | ... | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 2 | 1.0 | 1 | 1 | 38.0 | 1 | 0 | PC 17599 | 4.266662 | C85 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 2 | 3 | 1.0 | 3 | 1 | 26.0 | 0 | 0 | STON/O2. 3101282 | 2.070022 | NaN | ... | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 3 | 4 | 1.0 | 1 | 1 | 35.0 | 1 | 0 | 113803 | 3.972177 | C123 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 4 | 5 | 0.0 | 3 | 0 | 35.0 | 0 | 0 | 373450 | 2.085672 | NaN | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
5 rows × 22 columns
5.3 Cabin
dataset['Cabin'].head()0 NaN
1 C85
2 NaN
3 C123
4 NaN
Name: Cabin, dtype: objectdataset['Cabin'].describe()count 292
unique 186
top G6
freq 5
Name: Cabin, dtype: objectdataset['Cabin'].isnull().sum()1007Cabin에 292개의 값이 있고 Null 값이 1007개 있는 것으로 확인된다. 여기서 필자는 Cabin의 앞 글자(알파벳)에 따른 생존률을 알아보려한다.
dataset['Cabin'][dataset['Cabin'].notnull()].head()1 C85
3 C123
6 E46
10 G6
11 C103
Name: Cabin, dtype: objectdataset['Cabin'] = pd.Series([i[0] if not pd.isnull(i) else 'X' for i in dataset['Cabin']])sns.countplot(dataset['Cabin'], order=['A', 'B', 'C', 'D', 'E', 'F', 'G', 'T', 'X'])<matplotlib.axes._subplots.AxesSubplot at 0x7fedd8ae80d0>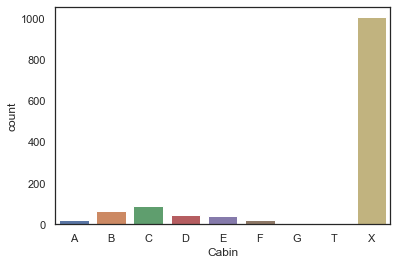
g = sns.factorplot('Cabin', 'Survived', data=dataset, kind='bar', size=6, palette='muted', order=['A', 'B', 'C', 'D', 'E', 'F', 'G', 'T', 'X'])
g.set_ylabels('Survival Probability')<seaborn.axisgrid.FacetGrid at 0x7fedd72f6760>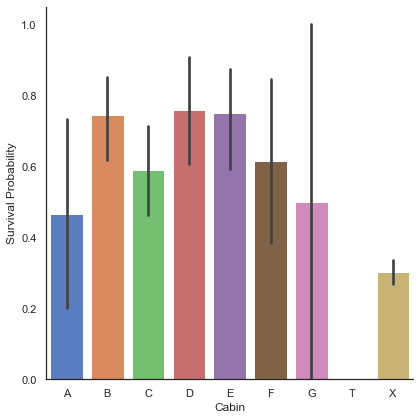
여기서 우리는 선실이 미확인된 승객(X)보단 B, C, D, E, F 선실 승객의 생존률이 더 높은 것을 알 수 있다. Cabin 에 대해서도 One-Hot encoding을 한다.
dataset = pd.get_dummies(dataset, columns=['Cabin'], prefix='Cabin')5.4 Ticket
dataset['Ticket'].head()0 A/5 21171
1 PC 17599
2 STON/O2. 3101282
3 113803
4 373450
Name: Ticket, dtype: object필자는 Ticket의 숫자부분보다 앞부분이 더 많은 정보를 가지고 있을 것이라 판단하고 앞글자만 잘라내기로 한다.
- isalpha: 문자열인지 아닌지를 True, False로 리턴
- isdigit: 숫자인지 아닌지를 True, False로 리턴
- strip: 양쪽의 공백 제거
Ticket = []
for i in list(dataset.Ticket):
if not i.isdigit():
Ticket.append(i.replace('.','').replace('/','').strip().split(' ')[0])
else:
Ticket.append('X')
dataset['Ticket'] = Ticket
dataset['Ticket'].head()0 A5
1 PC
2 STONO2
3 X
4 X
Name: Ticket, dtype: objectTicket 과 Pclass 에 대해 One-Hot encoding을 진행한다. Pclass 는 그 전에 categorical value 로 바꿔준다. 그리고 필요없는 정보인 PassengerId 를 삭제한다.
dataset = pd.get_dummies(dataset, columns=['Ticket'], prefix='T')
dataset['Pclass'] = dataset['Pclass'].astype('category')
dataset = pd.get_dummies(dataset, columns=['Pclass'], prefix='Pc')dataset.drop(labels=['PassengerId'], axis=1, inplace=True)dataset.head()| Survived | Sex | Age | SibSp | Parch | Fare | Fsize | Single | SmallF | MedF | ... | T_STONO | T_STONO2 | T_STONOQ | T_SWPP | T_WC | T_WEP | T_X | Pc_1 | Pc_2 | Pc_3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0 | 22.0 | 1 | 0 | 1.981001 | 2 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1.0 | 1 | 38.0 | 1 | 0 | 4.266662 | 2 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 1.0 | 1 | 26.0 | 0 | 0 | 2.070022 | 1 | 1 | 0 | 0 | ... | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 1.0 | 1 | 35.0 | 1 | 0 | 3.972177 | 2 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0.0 | 0 | 35.0 | 0 | 0 | 2.085672 | 1 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
5 rows × 67 columns
이것으로 모든 데이터 처리는 끝났다.
6. Modeling
train = dataset[:train_len]
test = dataset[train_len:]
test.drop(labels=['Survived'], axis=1, inplace=True)train['Survived'] = train['Survived'].astype(int)
Y_train = train['Survived']
X_train = train.drop(labels=['Survived'], axis=1)6.1 Simple Modeling
6.1.1 Cross Validate Models
유명한 10개의 분류기를 비교하고 Stratified KFold로 교차 검증을 진행한다.
- SVC
- Decision Tree
- AdaBoost
- Random Forest
- Extra Trees
- Gradient Boosting
- Multiple layer perceptron(neural network)
- KNN
- Logistic Regression
- Linear Discriminant Analysis
kfold = StratifiedKFold(n_splits=10)
random_state = 2
classifiers = []
classifiers.append(SVC(random_state=random_state))
classifiers.append(DecisionTreeClassifier(random_state=random_state))
classifiers.append(AdaBoostClassifier(DecisionTreeClassifier(random_state=random_state), random_state=random_state, learning_rate=0.1))
classifiers.append(RandomForestClassifier(random_state=random_state))
classifiers.append(ExtraTreesClassifier(random_state=random_state))
classifiers.append(GradientBoostingClassifier(random_state=random_state))
classifiers.append(MLPClassifier(random_state=random_state))
classifiers.append(KNeighborsClassifier())
classifiers.append(LogisticRegression(random_state=random_state))
classifiers.append(LinearDiscriminantAnalysis())
cv_results = []
for classifier in classifiers:
cv_results.append(cross_val_score(classifier, X_train, y=Y_train, scoring='accuracy', cv=kfold, n_jobs=4))
cv_means = []
cv_std = []
for cv_result in cv_results:
cv_means.append(cv_result.mean())
cv_std.append(cv_result.std())
cv_res = pd.DataFrame({'CrossValMeans': cv_means, 'CrossValerrors': cv_std, 'Algorithm': ["SVC","DecisionTree","AdaBoost",
"RandomForest","ExtraTrees","GradientBoosting","MultipleLayerPerceptron","KNeighboors","LogisticRegression","LinearDiscriminantAnalysis"]})
# **kwargs의 의미는 어떤 값을 넣을진 모르는데 변수가 딕셔너리 형태로 입력되는 것, *args는 변수가 튜플 형태로 입력되는 것
g = sns.barplot('CrossValMeans', 'Algorithm', data=cv_res, palette='Set3', orient='h', **{'xerr':cv_std})
g.set_xlabel('Mean Accuracy')
g = g.set_title('Cross Validation Scores')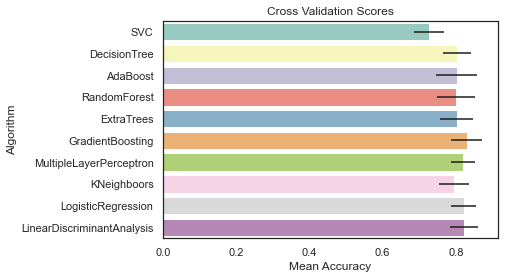
필자는 여기서 SVC, AdaBoost, RandomForest, ExtraTrees, GradientBoosting 을 앙상블 모델링을 위해 선택한다.
6.1.2 Hyperparameter Tunning for Best Models
# AdaBoost
DTC = DecisionTreeClassifier()
adaDTC = AdaBoostClassifier(DTC, random_state=7)
ada_param_grid = {'base_estimator__criterion': ['gini', 'entropy'],
'base_estimator__splitter': ['best', 'random'],
'algorithm': ['SAMME', 'SAMME.R'],
'n_estimators': [1, 2],
'learning_rate': [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3, 1.5]}
# verbose=0(default)면 메시지 출력 안함, 1이면 간단한 메시지 출력, 2면 하이퍼 파라미터별 메시지 출력
gsadaDTC = GridSearchCV(adaDTC, param_grid=ada_param_grid, cv=kfold, scoring='accuracy', n_jobs=4, verbose=1)
gsadaDTC.fit(X_train, Y_train)
ada_best = gsadaDTC.best_estimator_
gsadaDTC.best_score_Fitting 10 folds for each of 112 candidates, totalling 1120 fits
[Parallel(n_jobs=4)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=4)]: Done 280 tasks | elapsed: 1.0s
[Parallel(n_jobs=4)]: Done 1120 out of 1120 | elapsed: 3.3s finished
0.8241317671092953# ExtraTrees
ExtC = ExtraTreesClassifier()
ex_param_grid = {"max_depth": [None],
"max_features": [1, 3, 10],
"min_samples_split": [2, 3, 10],
"min_samples_leaf": [1, 3, 10],
'bootstrap': [False],
'n_estimators': [100, 300],
'criterion': ['gini']}
gsExtC = GridSearchCV(ExtC, param_grid=ex_param_grid, cv=kfold, scoring='accuracy', n_jobs=4, verbose=1)
gsExtC.fit(X_train, Y_train)
ExtC_best = gsExtC.best_estimator_
gsExtC.best_score_Fitting 10 folds for each of 54 candidates, totalling 540 fits
[Parallel(n_jobs=4)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=4)]: Done 42 tasks | elapsed: 3.7s
[Parallel(n_jobs=4)]: Done 192 tasks | elapsed: 11.4s
[Parallel(n_jobs=4)]: Done 442 tasks | elapsed: 27.6s
[Parallel(n_jobs=4)]: Done 540 out of 540 | elapsed: 33.9s finished
0.8308733401430031# RandomForest
RFC = RandomForestClassifier()
rf_param_grid = {'max_depth': [None],
'max_features': [1, 3, 10],
'min_samples_split': [2, 3, 10],
'min_samples_leaf': [1, 3, 10],
'bootstrap': [False],
'n_estimators': [100, 300],
'criterion': ['gini']}
gsRFC = GridSearchCV(RFC, param_grid=rf_param_grid, cv=kfold, scoring='accuracy', n_jobs=4, verbose=1)
gsRFC.fit(X_train, Y_train)
RFC_best = gsRFC.best_estimator_
gsRFC.best_score_Fitting 10 folds for each of 54 candidates, totalling 540 fits
[Parallel(n_jobs=4)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=4)]: Done 42 tasks | elapsed: 4.2s
[Parallel(n_jobs=4)]: Done 192 tasks | elapsed: 12.8s
[Parallel(n_jobs=4)]: Done 442 tasks | elapsed: 30.6s
[Parallel(n_jobs=4)]: Done 540 out of 540 | elapsed: 37.6s finished
0.8354315628192033# GradientBoosting
GBC = GradientBoostingClassifier()
gb_param_grid = {'loss': ['deviance'],
'n_estimators': [100, 200, 300],
'learning_rate': [0.1, 0.05, 0.01],
'max_depth': [4, 8],
'min_samples_leaf': [100, 150],
'max_features': [0.3, 0.1]}
gsGBC = GridSearchCV(GBC, param_grid=gb_param_grid, cv=kfold, scoring='accuracy', n_jobs=4, verbose=1)
gsGBC.fit(X_train, Y_train)
GBC_best = gsGBC.best_estimator_
gsGBC.best_score_Fitting 10 folds for each of 72 candidates, totalling 720 fits
[Parallel(n_jobs=4)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=4)]: Done 42 tasks | elapsed: 2.2s
[Parallel(n_jobs=4)]: Done 336 tasks | elapsed: 11.7s
[Parallel(n_jobs=4)]: Done 720 out of 720 | elapsed: 24.3s finished
0.8297497446373849# SVC
SVMC = SVC(probability=True)
svc_param_grid = {'kernel': ['rbf'],
'gamma': [0.001, 0.01, 0.1, 1],
'C': [1, 10, 50, 100, 200, 300, 1000]}
gsSVMC = GridSearchCV(SVMC, param_grid=svc_param_grid, cv=kfold, scoring='accuracy', n_jobs=4, verbose=1)
gsSVMC.fit(X_train, Y_train)
SVMC_best = gsSVMC.best_estimator_
gsSVMC.best_score_Fitting 10 folds for each of 28 candidates, totalling 280 fits
[Parallel(n_jobs=4)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=4)]: Done 42 tasks | elapsed: 2.5s
[Parallel(n_jobs=4)]: Done 192 tasks | elapsed: 13.3s
[Parallel(n_jobs=4)]: Done 280 out of 280 | elapsed: 23.1s finished
0.83313329928498476.1.3 Plot Learning Curves
Learning Curve 는 훈련 세트에 대한 과적합 효과와 훈련 크기가 정확도에 미치는 영향을 확인하기 좋은 방법이다.
# np.linspace(시작값, 끝값, 갯수) 갯수 안쓰면 50개
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=-1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel('Training Examples')
plt.ylabel('Score')
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
# 그래프에 격자 표시 넣기
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color='r')
plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color='r', label='Traing Score')
plt.plot(train_sizes, test_scores_mean, 'o-', color='g', label='Cross-Validation Score')
plt.legend(loc='best')
return plt
plot_learning_curve(gsRFC.best_estimator_, 'RF Mearning Curves', X_train, Y_train, cv=kfold)
plot_learning_curve(gsExtC.best_estimator_,"ExtraTrees Learning Curves", X_train, Y_train, cv=kfold)
plot_learning_curve(gsSVMC.best_estimator_,"SVC Learning Curves", X_train, Y_train, cv=kfold)
plot_learning_curve(gsadaDTC.best_estimator_,"AdaBoost Learning Curves", X_train, Y_train, cv=kfold)
plot_learning_curve(gsGBC.best_estimator_,"GradientBoosting Learning Curves", X_train, Y_train, cv=kfold)<module 'matplotlib.pyplot' from '/Users/andylee/opt/anaconda3/lib/python3.8/site-packages/matplotlib/pyplot.py'>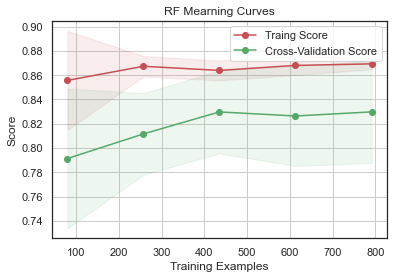
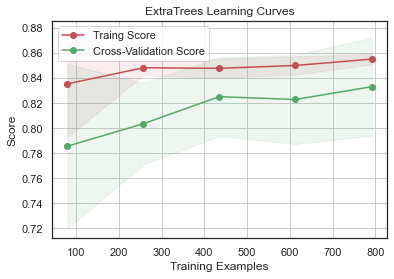
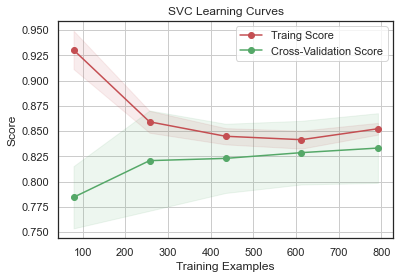
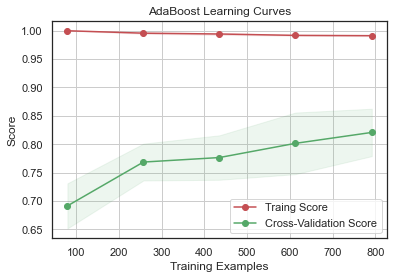
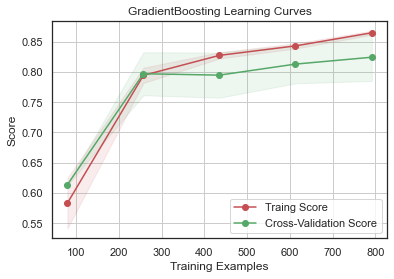
GradientBoosting 과 AdaBoost 에서 과적합의 경향을 보이고 SVC 와 ExtraTrees 는 Training Score 와 Cross-Validation Score 가 가까워서 예측을 더 일반화하는 것으로 보인다.
6.1.4 Feature importance of tree based classifiers
4개의 분류기에 대해 각각 어떠한 피쳐가 중요했는지에 대해 알아보자.
# sharex: 모든 서브플롯이 같은 x축 눈금을 사용하도록 함.
nrows = ncols = 2
f, ax = plt.subplots(nrows=nrows, ncols=ncols, sharex='all', figsize=(15, 15))
names_classifiers = [('AdaBoosting', ada_best), ('ExtraTrees', ExtC_best), ('RandomForest', RFC_best), ('GradientBoosting', GBC_best)]
nclassifier = 0
for row in range(nrows):
for col in range(ncols):
name = names_classifiers[nclassifier][0]
classifier = names_classifiers[nclassifier][1]
indices = np.argsort(classifier.feature_importances_)[::-1][:40]
g = sns.barplot(y=X_train.columns[indices][:40], x=classifier.feature_importances_[indices][:40], orient='h', ax=ax[row][col])
g.set_xlabel('Relative Importance', fontsize=12)
g.set_ylabel('Features', fontsize=12)
g.tick_params(labelsize=9)
g.set_title(name + ' Feature Importance')
nclassifier += 1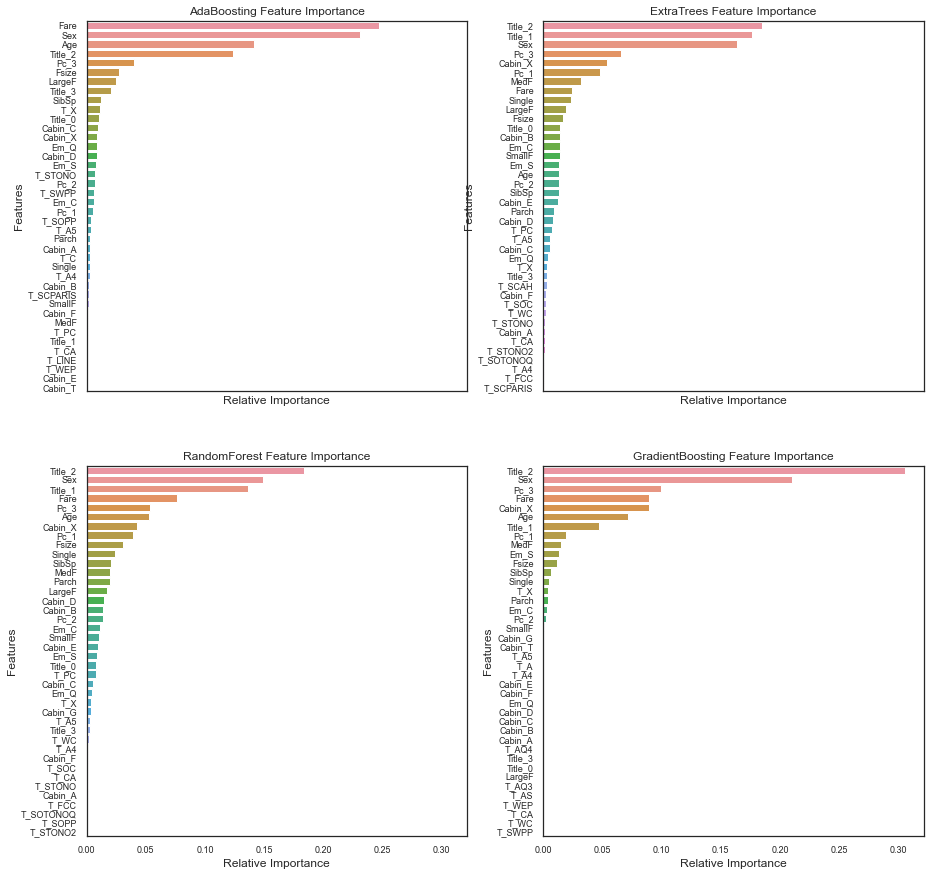
4 종류의 분류기는 각기 다른 특징(Fare, Title_2)을 중요하게 생각한다. 하지만 모든 분류기에서 Fare, Title_2(Miss~Mrs), Age, Sex 등은 모두 높은 중요도를 가진다.
여기까지 정리하면:
- Pc_1, Pc_2, Pc_3, Fare 는 승객들의 사회적 지위를 나타낸다.
- Sex, Title_2(Miss~Mrs), Title_3(Mr)는 성별을 나타낸다.
- Age, Title_1(Master)는 나이를 나타낸다.
- Fsize, LargeF, MedF, SmallF, Single은 가족의 크기를 나타낸다.
위 4 종류 분류기의 중요성에 따르면 생존률은 선박 안의 위치보다 연령, 성별, 가족 규모, 사회적 지위와 더 연관이 있다.
test_Survived_RFC = pd.Series(RFC_best.predict(test), name='RFC')
test_Survived_ExtC = pd.Series(ExtC_best.predict(test), name="ExtC")
test_Survived_SVMC = pd.Series(SVMC_best.predict(test), name="SVC")
test_Survived_AdaC = pd.Series(ada_best.predict(test), name="Ada")
test_Survived_GBC = pd.Series(GBC_best.predict(test), name="GBC")
ensemble_results = pd.concat([test_Survived_RFC,test_Survived_ExtC,test_Survived_AdaC,test_Survived_GBC, test_Survived_SVMC],axis=1)
sns.heatmap(ensemble_results.corr(), annot=True, cmap='summer_r')<matplotlib.axes._subplots.AxesSubplot at 0x7fedd491f910>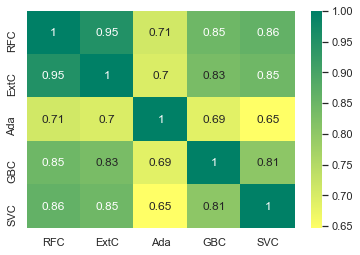
AdaBoost 를 제외한 나머지 분류기들은 매우 큰 상관관계가 있다. AdaBoost 의 상관관계도 많이 낮은 것은 아니기에 다수결 분석을 진행할만 하다.
6.2 Ensemble modeling
VotingClassifier 는 다수결 분류로 두가지 방법이 가능하다.(5가지 분류기가 있을때를 가정)
- hard voting: 1이라고 예측한 분류기가 3개, 0이라고 예측한 분류기가 2개라면 1을 채택한다. -> 과반수 투표
- soft voting: 각 분류기의 예측을 평균내어 예측 확률에 대한 평균이 높게 나오는 클래스를 최종 예측 클래스로 정한다.
여기선 soft voting 방식을 사용한다.
votingC = VotingClassifier(estimators=[('rfc', RFC_best), ('extc', ExtC_best), ('svc', SVMC_best), ('adac', ada_best), ('gbc', GBC_best)], voting='soft', n_jobs=4)
votingC = votingC.fit(X_train, Y_train)6.3 Prediction
test_Survived = pd.Series(votingC.predict(test), name='Survived')
results = pd.concat([IDtest, test_Survived], axis=1)
results.to_csv('titanic_with_ensemble_modeling.csv', index=False)