추천시스템의 종류

1. Collaborative Filtering
□ 메모리 기반 접근 (Neighborhood-based)
☑ 모델 기반 접근 Explicit
□ 모델 기반 접근 Implicit, MF-based
□ 모델 기반 접근 Implicit, Metric / Deep learning-based
2. Side Information-based Recommendation
□ 컨텐츠 기반 추천
□ 컨텐츠 기반 Collaborative Filtering

지난 컨텐츠에서는 메모리 기반 CF 모델들을 살펴봤다. 메모리 기반 CF의 가장 큰 단점은 추정을 위해 실제 값들을 활용하기 보다는, 유저/아이템 간의 유사도라는 Heuristic을 사용한다는 단점이 있었다. 이번 글에서는 이와 달리 직접적으로 평점 추정을 위해 직접적으로 Implicit/Explicit 데이터를 활용하는 Model-based CF 방법에 대해 알아본다.

Explicit Feedback의 Model-based 접근

1. MF (Matrix Factorization)

Explicit Feedback은 사용자가 아이템에 대한 선호도를 직접적으로 밝힌 데이터셋이다. Matrix Factorization의 기본 가정은; 관찰할 수는 없지만 유저와 아이템에게도 각각 내재된 요인들이 있다는 것이다. 가령 Leo가 Titanic에 대해 내린 평점이 5라고 할때, Leo에게 장르별 선호도가 있고, Titanic이라는 영화에도 장르별 속성이 있을 것이며, 이 두 행렬을 element-wise하게 곱한 값이 평점인 '5'라는 것이다.

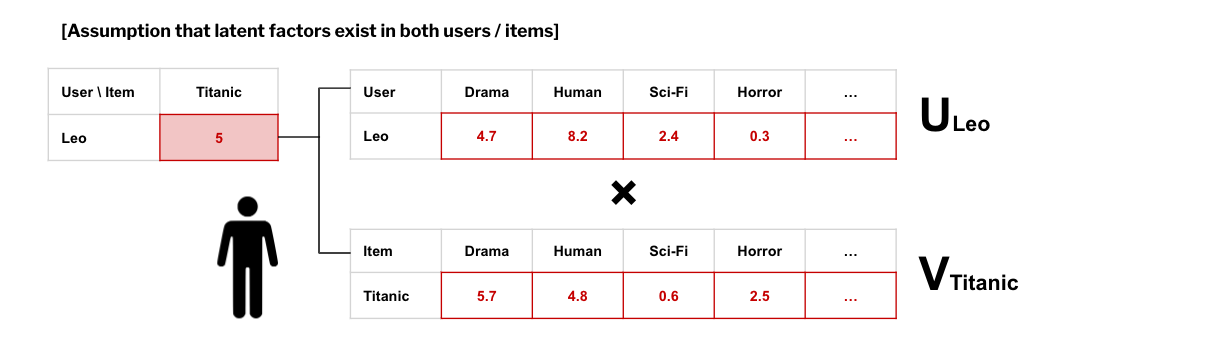
Leo와 Titanic가 각각 잠재된 속성 행렬로 분해될 수 있다면, 모든 유저와 아이템에 대해서도 분해된 행렬로 표현할 수 있을 것이다. 이것이 추천시스템에서 Matrix Factorization이다. MF를 통해 $U$와 $V$행렬을 알아낼 수 있다면, $R*$를 추정할 수 있게 된다.

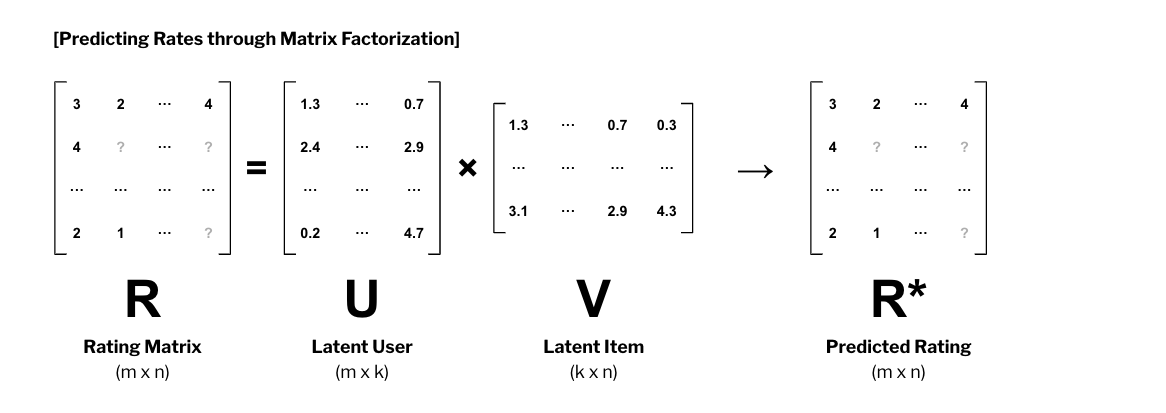
2. SVD++ (Singular Value Decomposition)

행렬 분해는 여러가지 방식으로 할 수 있지만, 그 중 가장 널리 활용되는 방법은 SVD(Singular Value Decomposition)이다. SVD는 행렬 $X$를 두 개의 Orthogonal Matrix와 하나의 Rectangular Matrix로 분리한다.

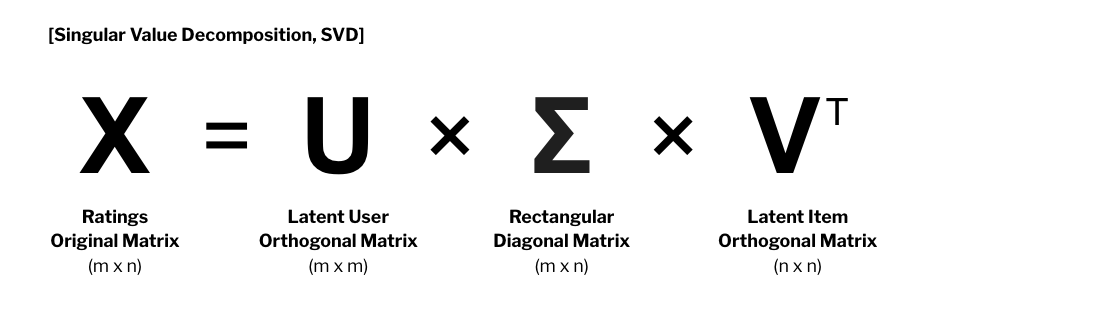
SVD 사용 이유

SVD를 사용하는 이유는 이것을 분해하는 과정보다 분해된 것을 다시 조합하는 데 있다. $U,V,\Sigma$로 분리된 행렬은 $\Sigma$의 특이값 $k$개만을 이용해 같은 크기의 행렬 $X$로 부분 복원 할 수 있기 때문이다. 따라서 결정적인 최대값 몇 개만으로도 $X$와 유사한 $X'$을 추정할 수 있게 된다. 그렇게 되면 $X$에서는 미지수였던, 아직 평점이 매겨지지 않은 항목들을 추정할 수 있게 된다.

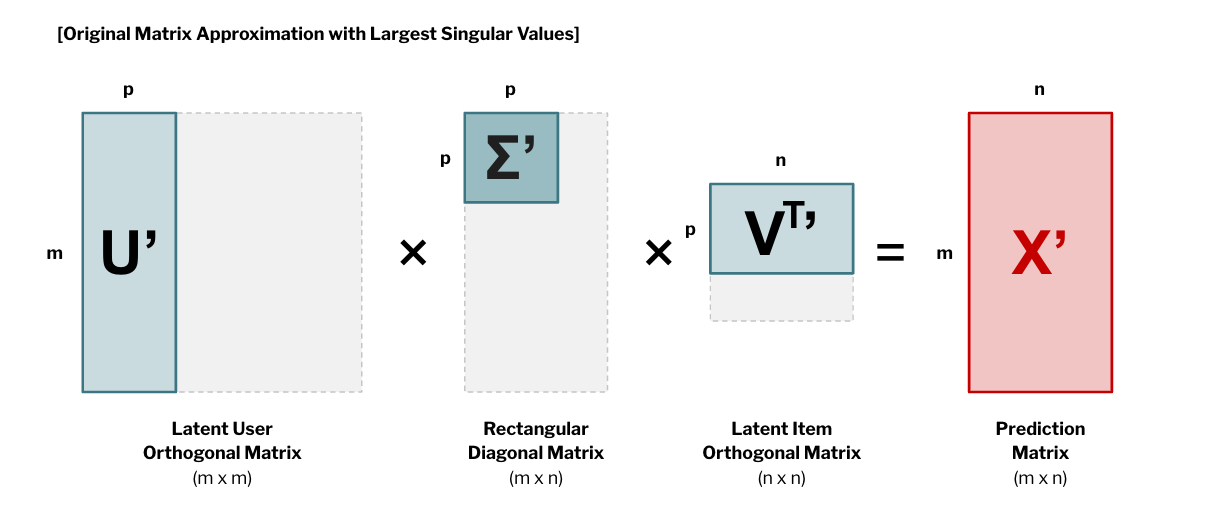
SVD의 단점

• 미지의 평점을 0 처리하게 되면 예측 성능이 떨어진다.
  SVD를 단순 적용한다고 하면, 모르는 값들을 '0'처리해 행렬에 반영하게 된다. 대부분의 경우 $X$는 Sparse하기 때문에 행렬의 대부분이 0으로 채워지게 된다.
• 예측값이 범위를 넘어서는 케이스가 많다.
  SVD는 평점의 범위(e.g. 0~5)를 감안해 계산하지 못한다. 따라서 음수나, 5이상의 값이 등장하기도 한다.

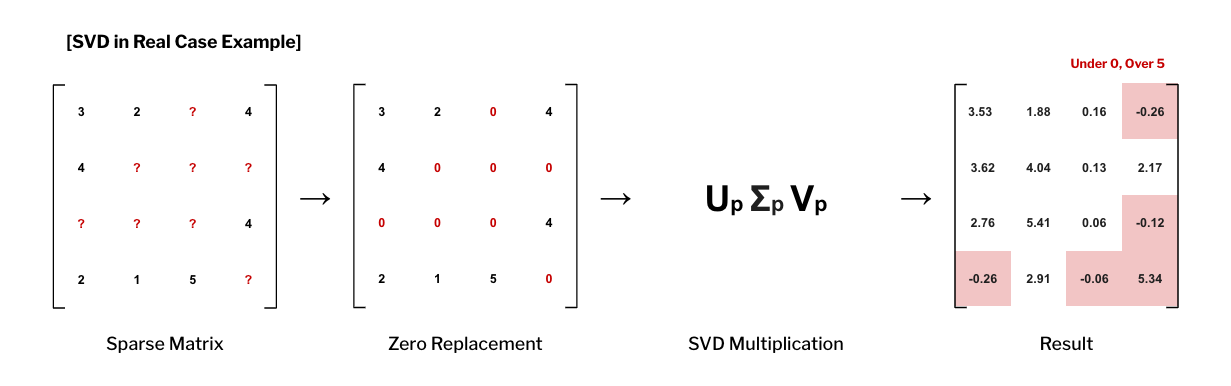
SVD++으로 극복

위 문제를 Optimization을 통해 해결하고자 SVD를 개선해 등장한 것이 SVD++다. 이전에는 Matrix안에 있는 모든 값을 사용했다면, 이번에는 유저 $u$가 아이템 $i$에 대해 평점을 매긴 항목에 한정해 계산한다. 실제 평점 $r_{ui}$와 유저 $u$의 latent vector $p_u$, 아이템 $i$의 latent vector $q_i$의 차이를 최소화 하는 $p_u$와 $q_i$ 찾도록 한다.

Target Optimization Fuction

• $L = min\frac{1}{2}\sum_{(u,i)\in R}(r_{ui}-p_uq_i^T)^2 +\lambda(|p_u|^2+|q_i|^2)$

Solved by Stochastic Gradient Descent

• $p_u \leftarrow p_u-\eta(-(r_{ui}-p_uq_i^T)q_i)+\lambda p_u$
• $q_i \leftarrow q_i-\eta(-(r_{ui}-p_uq_i^T)p_u)+\lambda q_i$

3. PMF (Probabilistic Matrix Factorization)

위에서 설명한 MF나 SVD++와 달리 데이터의 확률적 분포를 고려해 개발한 Matrix Factorization도 있다. 바로 PMF다. PMF는 각 유저와 아이템의 latent vector을 곱한 값을 평균으로, $\sigma^2$를 분산으로 가진 정규분포의 곱으로 구성된다고 가정하고 있다. $R_{ij}$의 구성요소인 $U$와 $V$또한 평균이 0, 분산이 $\sigma^2_U,\sigma^2_V$인 정규분포로 구성되어 있다고 가정하고 있다. 이러한 가정들에 따라 각각의 확률 변수를 정의한다. 이 알고리즘도 마찬가지로 관찰값이 있는 데이터에 대해서만 적용한다.

Joint PDF for rating vector R

$p(R|U,V, \sigma^2)=\Pi^N_{i=1}\Pi^M_{j=1}[\Nu(R_{ij}|U_i^TV_j,\sigma^2)]^{l_{ij}}$

Joint PDF for user vector U, item vector V

(i) $\;\;\;p(U|\sigma^2_U)=\Pi^N_{i=1}N(U_i|0,\sigma^2_UI)$

(ii) $\;\;\;p(U|\sigma^2_V)=\Pi^M_{j=1}N(V_i|0,\sigma^2_VI)$

Notations

Variable	Note
$U$	User Latent Matrix
$V$	Item Latent Matrix
$\sigma^2$	Variable (Hyperparameter)
$R_{ij}$	유저i의 아이템j에 대한 점수
$U^T_i$	유저 i의 Latent Vector, Transposed
$V_j$	아이템 j의 Lantent Vector
$I_{ij}$	Identity Function,i의 j에 대한 점수가 있으면 1, 없으면 0
$N$	유저 수
$M$	아이템 수
$D$	Latent 변수 개수

위에서 정의한 확률 변수들을 베이즈 정리($p(A|B)=P(B|A)P(A)P(B)$)에 따라 다음과 같이 목적함수 $E$를 정리할 수 있다. 그리고 위 SVD++와 같이 목적함수를 최소화시키는 Stochastic Gradient Descent로 푼다.

Target Optimization Fuction

(1) $\;\;\;p(U,V|R,\sigma^2,\sigma^2_U,\sigma^2_V) \propto p(R|U,V,\sigma^2)p(U|\sigma^2_U)p(V|\sigma^2_V)$

(2) $\;\;\;ln\,p(U,V|R,\sigma^2,\sigma^2_U,\sigma^2_V)= ln\,p(R|U,V,\sigma^2)+ln\,p(U|\sigma^2_U)+ln\,p(V|\sigma^2_V)$

(3) $\;\;\;ln\,p(U,V|R,\sigma^2,\sigma^2_U,\sigma^2_V)=E$

(4) $\;\;\;E=\frac{1}{2}\sum^N_{i=1}\sum^M_{j=1}I_{ij}(R_{ij}-U^T_iV_j)^2+\frac{\lambda_U}{2}\sum^N_{i=1}||U_i||^2_{Fro}+\frac{\lambda_V}{2}\sum^M_{j=1}||V_j||^2_{Fro}$

Solved by Stochastic Gradient Descent

• $\frac{\partial E}{\partial U_i}=\sum^M_{j=1}(I_{ij}(R_{ij}-U_i^TV_j))V_j+\lambda_UU_i$

• $\frac{\partial E}{\partial V_j}=\sum^N_{i=1}(I_{ij}(R_{ij}-U_i^TV_j))U_i+\lambda_VV_j$

---

Reference
특이값 분해, 공돌이의 수학정리노트 https://angeloyeo.github.io/2019/08/01/SVD.html
PMF, Hwani https://hwa-a-nui.tistory.com/27