해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/입니다.
이번에는, 모델의 출력이 연속적인 값으로 나오는 Regression에 대해 알아본다.
Linear Models
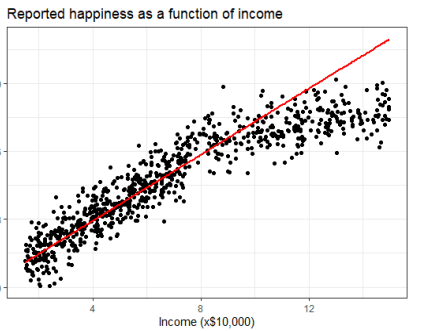
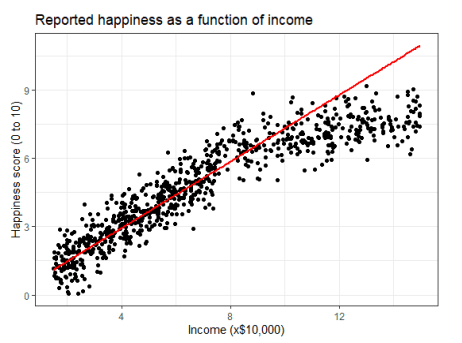
아래 그림은 수입에 따른 행복도를 조사한 결과 그래프이다.
많은 사람들이 수입이 증가함에 따라 행복도 증가할 것으로 예상하지만, 실제로는 그렇지 않다.
선형모델에서의 Hypothesis set H는 input feature와 model parameter의 linear combination으로 구성된다.
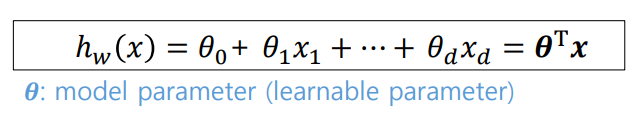
해당 식에서 θ (세타)는 모델의 파라미터를 나타내며, 학습가능한 파라미터라는 의미인 learnable parameter다.
linear model의 장점은 다음과 같다.
Simplicity: 모델이 단순하여 사용과 해석이 간단함Generalization: 모델이 결과값 도출에 있어 안정적 -> 변동이 심하지 않음
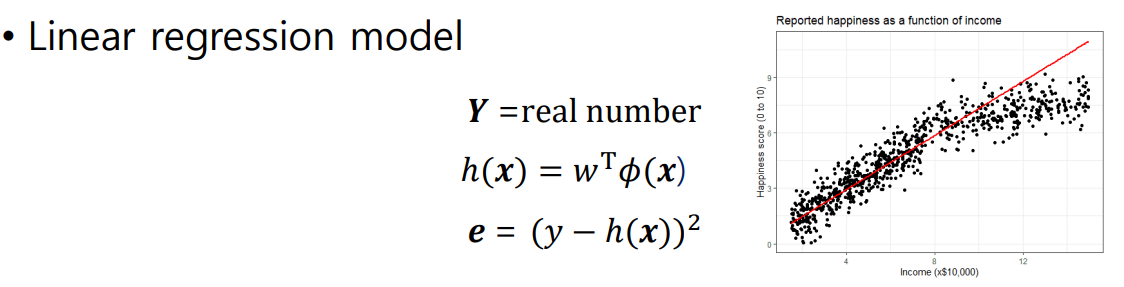
Feature Organization
인공지능 학습에 있어 feature를 추출하는 과정도 매우 중요하다. 별 의미 없는 feature를 사용할 경우, 인공지능 학습의 의미가 없을 수 있기 때문이다.
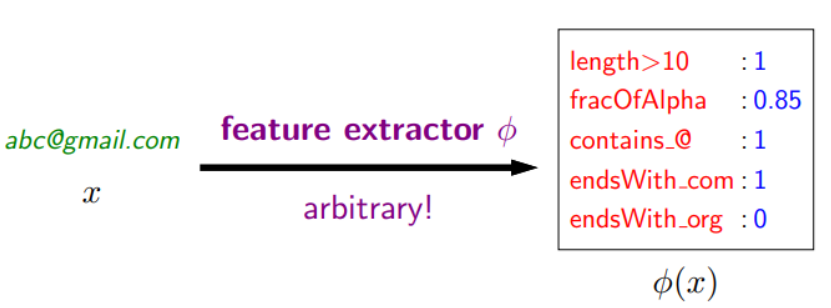
만약 위 그림과 같이 모델의 입력으로 이메일 주소가 들어온다고 가정할 경우, feature extractor를 통해 오른쪽 박스와 같이 입력의 다양한 특징을 추출할 수 있다.
위와 같이 입력 변수가 1개인 문제는 Univariate Problem이라고 하고,
입력 변수가 1개 이상인 문제는 Multivariate Problem이라고 한다.
Regression이 사용하는 데이터 샘플의 구성은 입력 X와 출력 Y로 구성되며, Y는 연속적인 값이 들어온다.
Linear Regression Framework
linear regression은, 주어진 입력에 대해 출력과의 선형적인 관계를 추론하는 문제다.
그에 대한 과정으로, 아래의 요소들을 고려해야 한다.
- 어떤 Predictor를 이용할 것인가? -
h(x) = θ_0 + θ_1X - Predictor의 성능은 어떠한가? -
MSE (Mean Square Error) 최소화 - 최고의 Predictor를 만드려면 어떻게 해야하는가? -
Gradient Descent,Normal Equation
Parameter Optimazation
파라미터를 최적화하는 것은 모델의 좋은 성능을 위해서 당연하다.
또한, 모델 파라미터 값에 따라 주어진 데이터에 fitting 하는 과정에서 오차가 발생할 수 있다.
아래는 파라미터 값에 따른 모델을 나타낸다. h(x) = θ_0 + θ_1X
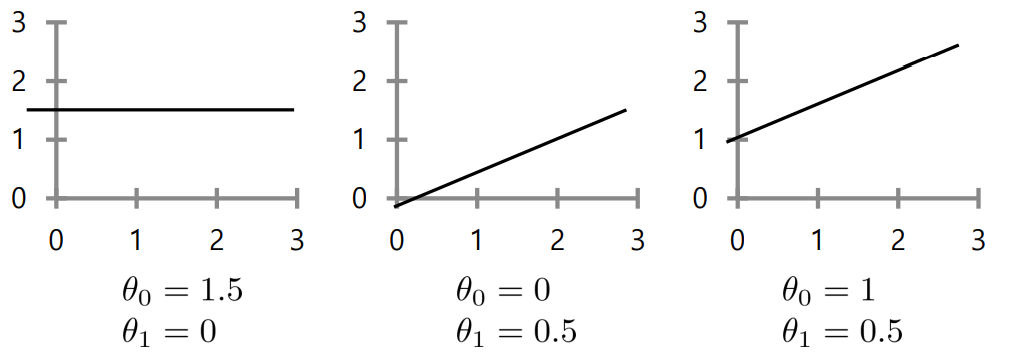
이 때 θ_0는 offset 으로 칭한다.
L2 Cost Function (Goal : minimizing MSE)
선형모델의 목적은 cost function을 최소화하는 θ_0, θ_1을 찾는 것이다.
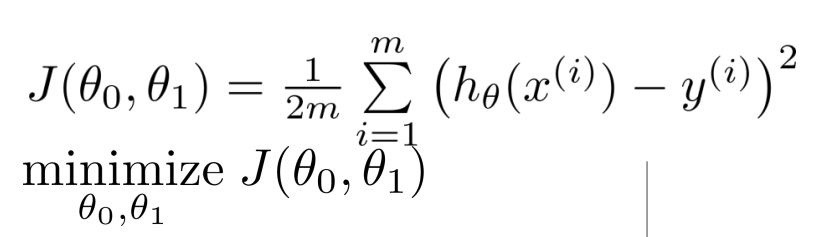
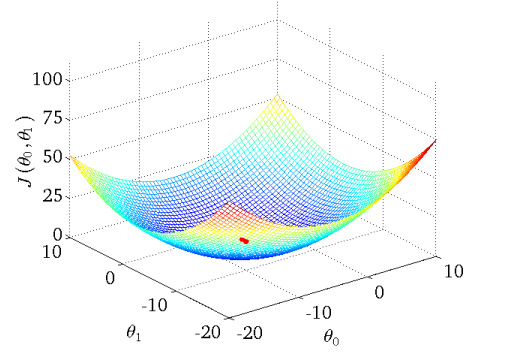
아래 그래프의 중심점에 있는, 세타들에 의해 cost function이 0이 되는 값의 확보가 목표다.
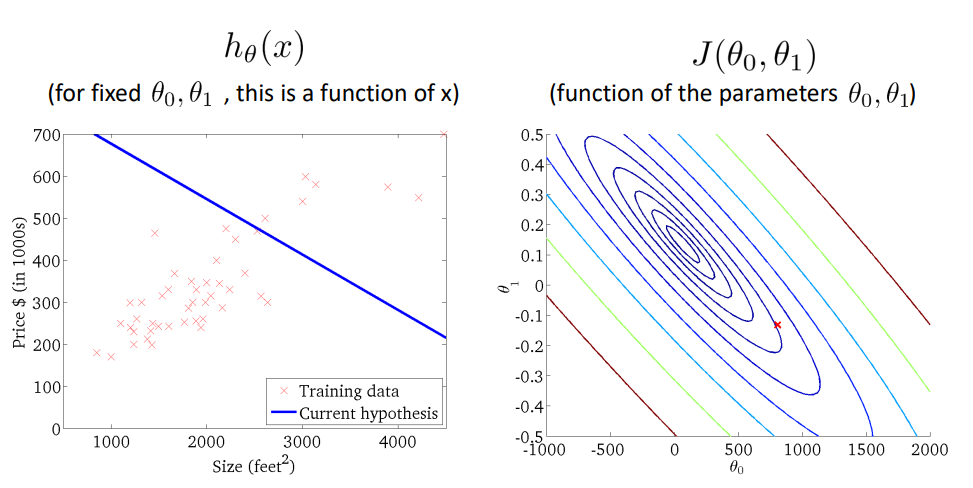
선형 모델의 학습과정에서 cost가 줄어드는 모습도 확인할 수 있다.
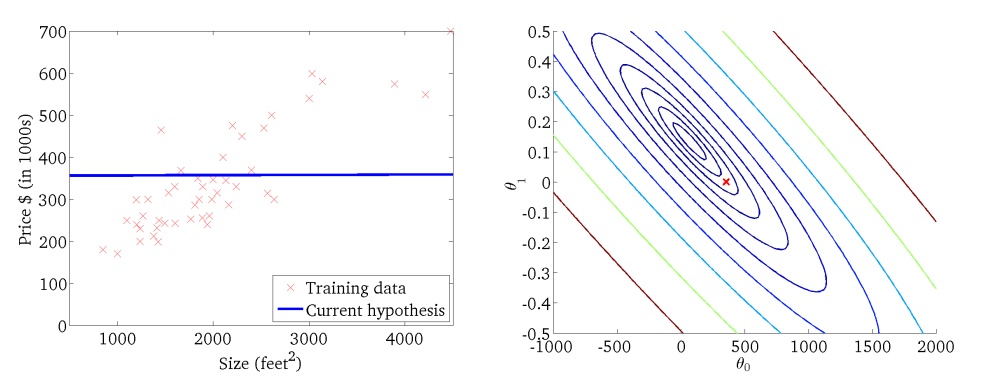
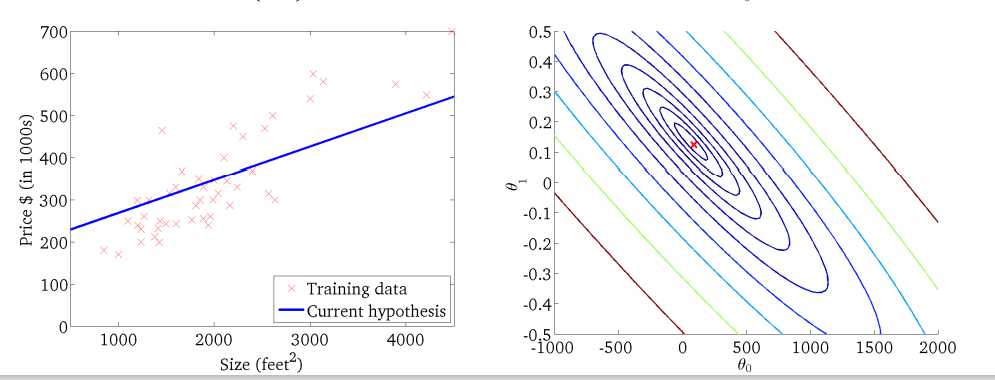
모델이 주어진 데이터의 패턴을 학습하며, 점점 cost function을 최소화하는 파라미터 세타를 찾아간다.
즉, cost function을 최소화 하는 세타를 구하는 과정이 Parameter Optimization 이다.
-
Y - Xθ에서,Xθ는score값으로 정의하며,(모델 출력 - 정답)^2을 평균내어In-sample error를 구한다. -
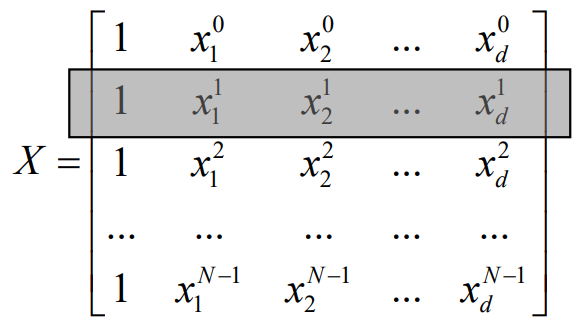
Target Vector y는 N차원의 벡터로, N개의 샘플마다 정답이 존재하기 때문에R^N으로 표현한다. -
Weight Vector θ는 θ_0가 존재하기 떄문에,R^(N+1)으로 표현한다.
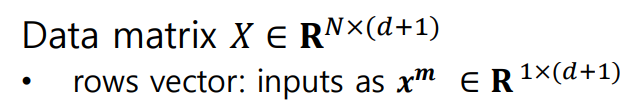
최적화가 완료된 파라미터 θ는 θ^*로 표현한다.
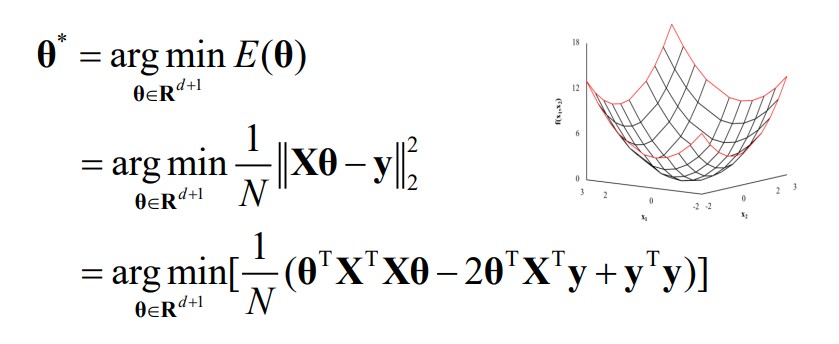
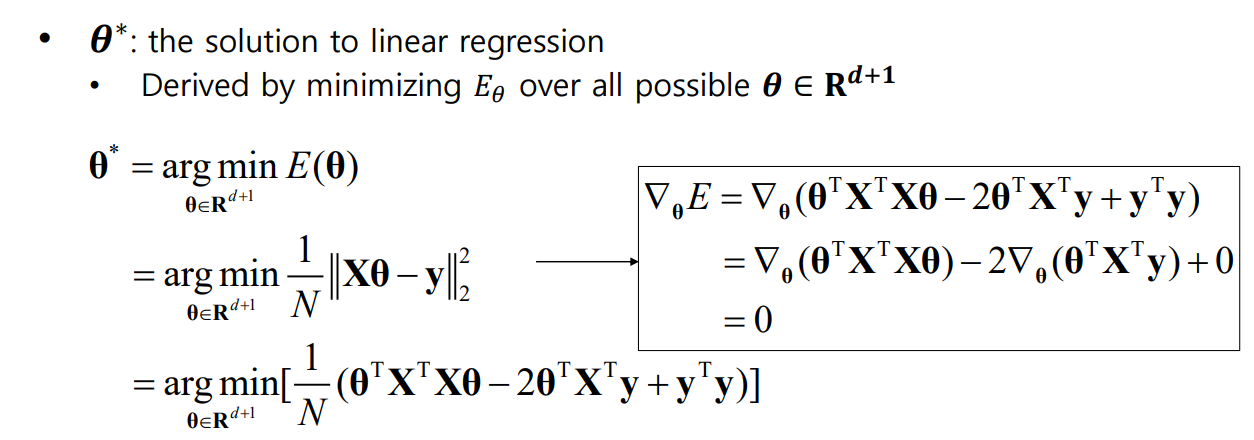
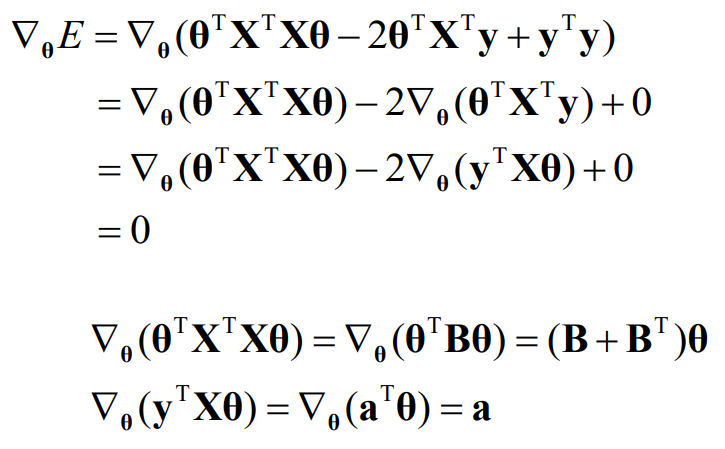
아래 수식 두 줄을 이용해 식을 전개하여, 정리한다.
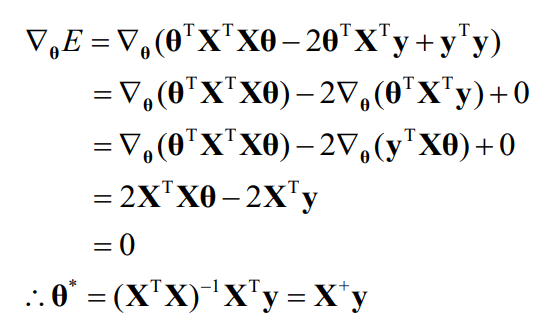
결론적으로, Normal Equation을 이용해 최적의 파라미터를 결정할 수 있는 식이 생성된다.
하지만, Normal Equation의 문제점은 데이터 샘플 숫자가 늘어나는 경우 전치행렬 등을 구하는 과정에서 너무 큰 오버헤드가 발생하여 효율적이지 못하며 전치행렬이 없는 데이터 샘플도 존재하기도 한다.
n이 증가 -> dimension 증가 -> metric 연산 중 큰 오버헤드 발생
이러한 문제점에 보다 잘하기 위해 Gradient Descent 방법을 도입한다.
Gradient는 함수를 미분하여 얻는 지표로, 해당 함수의 변화하는 정도를 표현하는 값이다.
gradient descent 방법에서는 반복과정을 통해 파라미터 θ를 바꾸며 gradient가 0인 지점을 찾아나선다.
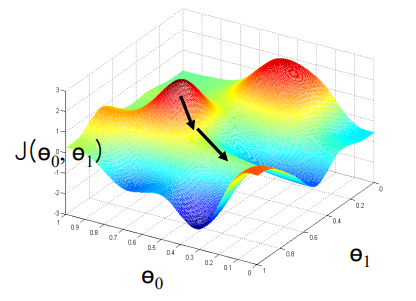
즉, 본 그림의 화살표와 같이 어떤 한 지점에서 하강 기울기가 가장 큰 쪽으로 반복적으로 내려가며,
error surface에서 가장 낮은 지점을 찾아가도록 하는 방법이다.
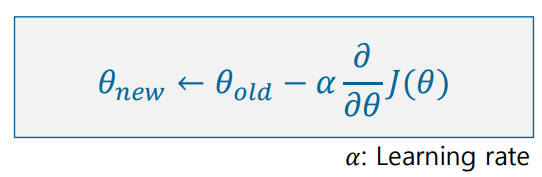
파라미터의 변경은 위의 식처럼 이루어지며, 이전 파라미터를 대체할 때, α값은 학습률을 뜻하며 파라미터 업데이트의 속도를 조절한다.
α가 크면 최소 지점에 수렴이 어렵고, 작으면 최소 지점에 수렴하기까지 오랜 시간이 걸린다.
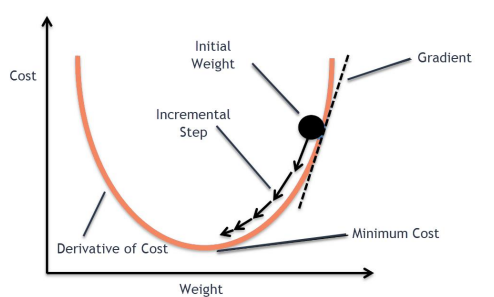
하지만, graient descent 방법에서 주의해야 할 부분이 있다.
아래 그림의 error surface의 두 라인 처럼 각 파라미터가 생각하는 최소 지점이 다를 수 있다.
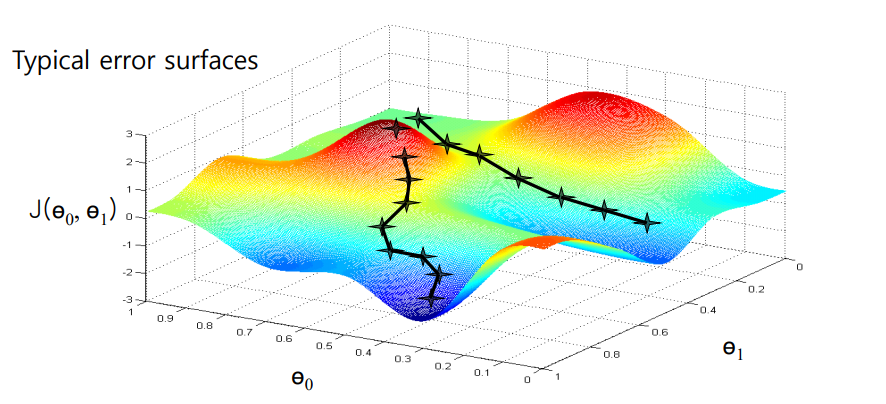
여기엔 global optimum, local optimum의 개념이 필요하다.
global optimum:error suface전체에서 가장 낮은 지점local optimum: 일정 지역에서는 최소 값이지만,global optimum보다 높은 지점
항상 local optimum에 빠지지 않도록 주의해야한다.
이를 해결하기 위한 방법으로, 데이터 샘플의 크기를 조정하는 stochastic gradient descent 방법이나, mini batch 등의 방법이 있으며, gradient descent 방법의 예로는 AdaGrad, RMSProp, Adam 등이 있다.
gradient descent의 수행 과정은 다음과 같다.
- 최적화하고자 하는
loss function정의 α와 같이 항상 양수의 값을 갖는hyperparameter정의loss function이 최소가 될 때까지 파라미터 업데이트 및 조정
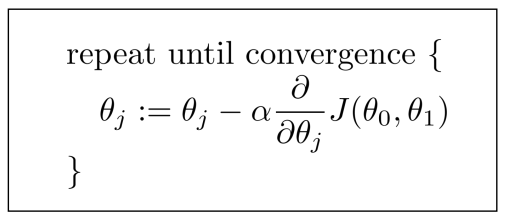
목적함수 J를 θ_J에 대해 미분한 결과와, θ_0, θ_1에 대해 미분한 결과다.
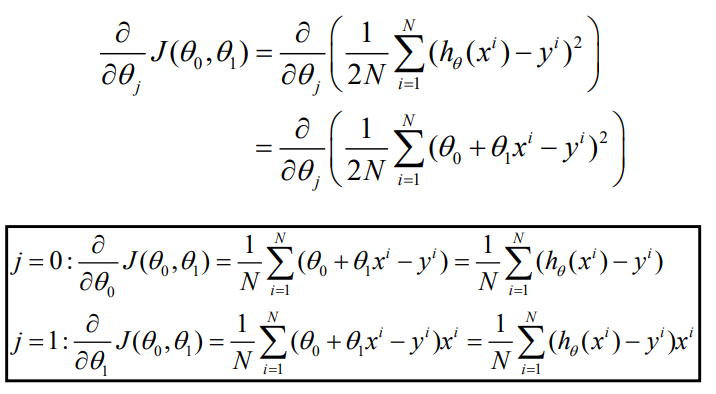
θ_0의 경우, 샘플들의 모든 에러를 측정한 후 더한뒤hyperparameter α를 통해 업데이트를 진행한다.θ_1의 경우,θ_0와 유사하지만, 에러 외에도 샘플을 곱하여 모두 더한뒤 업데이트를 진행한다.
