해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다.
이번에는 Gradient Descent 방법의 문제점을 보완한 기법들을 살펴본다.
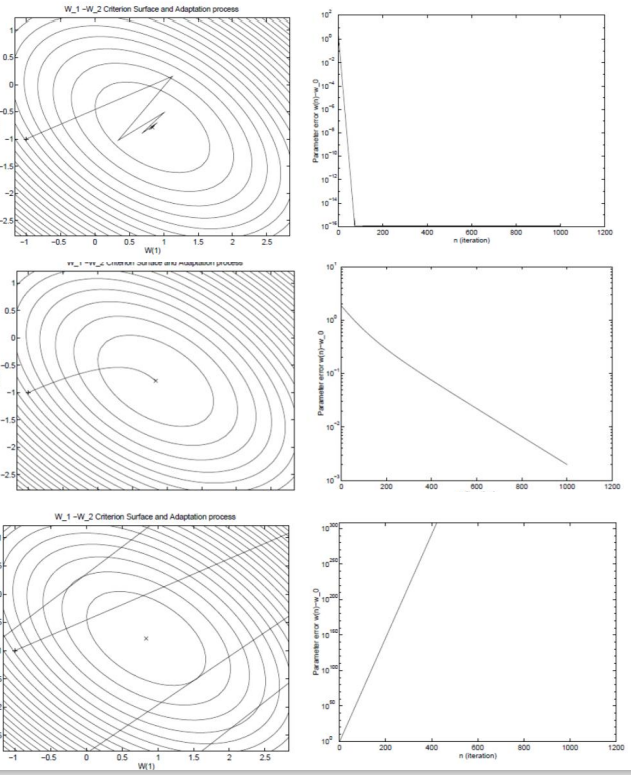
위 그림은 gradient descent의 학습률 α에 따른 학습 과정을 보인다.
위에서 부터 적당한 학습률, 작은 학습률, 큰 학습률이다.
- 적당한
α: 적절한 시간 내에error를 최소화하는 지점을 찾음 - 작은
α: 오랜 시간이 걸려error가 최소화되는 지점을 찾지만, 안정적으로 학습을 진행 - 큰
α: 시간과 관계없이error가 줄지않고, 오히려 늘어나는 형상을 보임
Batch Gradient Descent
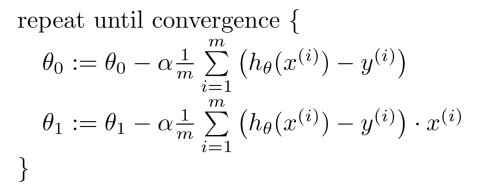
일반적인 gradient descent 방법으로, 파라미터가 업데이트 되며 점차 모델이 fitting한다.
해당 기법은 수식에도 나와있는 것 처럼 θ_0, θ_1의 업데이트 과정에서 전체 샘플 m개를 모두 고려해야 하기에 m이 증가할수록 복잡도 및 오버헤드가 크게 증가한다는 단점이 있다.
Stochastic Gradient Descent
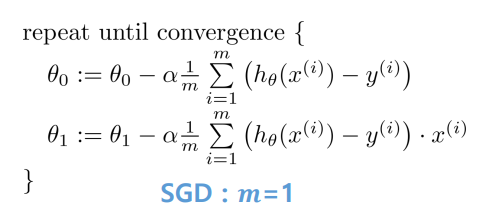
앞서 말한 일반적인 gradient descent 방법에서 m의 크기를 1로 고정시켜 놓은 방식으로, 빠르게 주기를 갱신할 수 있는 장점이 있다. 하지만 샘플 1개 1개 각각을 통해 파라미터를 계산하기 때문에, Noise의 영향을 잘 받는다.
m의 크기를 1 < m < N 으로 정해놓은 SGD를 mini-batch SGD라고 한다.
Gradient Descent Limitaion : Local Optimum
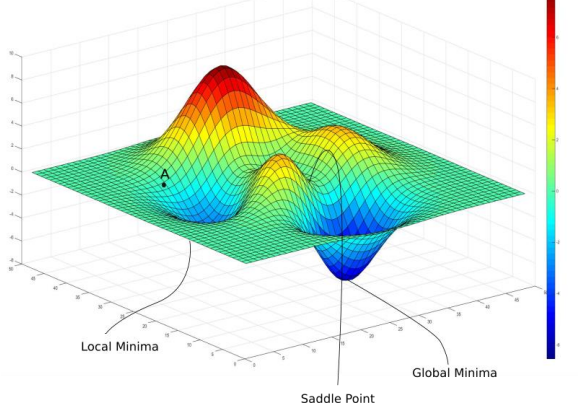
지난 시간에도 얘기 했지만, global optimum이 아닌, local optimum에 빠짐으로써 적절한 파라미터 세팅이 불가할 수 있다.
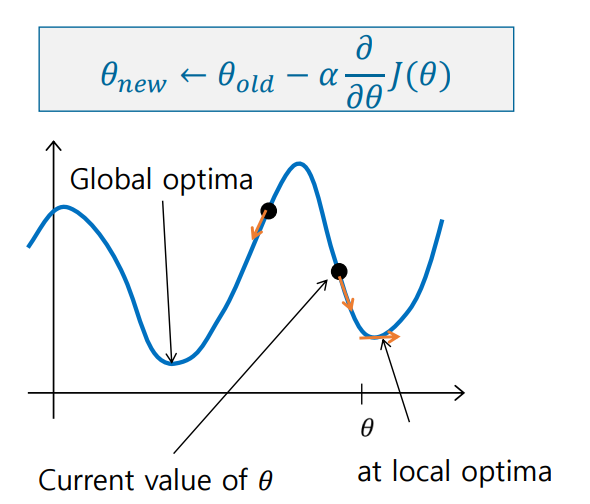
또한, 위 그림과 같이 시작 포인트의 위치에 따라 local optimum에 빠질 수 있다. 주로 이런 문제는 모델이 매우 복잡한 딥러닝 모델에서 주로 발생하며, 아래의 그림과 같이 Saddle Point라고 하는 gradient가 0인 구간도 존재한다.
Method of Momentum
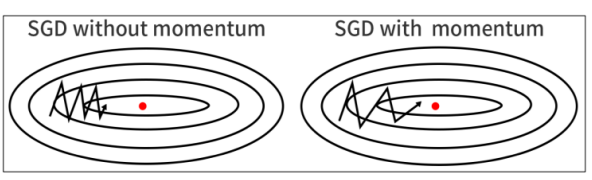
Momentum은 과거에 gradient가 업데이트 되던 방향 및 속도를 어느정도 반영해서 현재 포인트가 0이더라도 계속해서 학습을 진행할 수 있는 동력을 제공하는 것으로, gradient descent 방식을 보완해준다.
이와 같은 방식을 Exponentially Weighted Moving Average 방식으로 칭하며, saddle point나 작은 noise gradient 값에 영향을 크게 받지 않고 안정적으로 수렴할 수 있도록 한다.

momentum의 계산은 위의 식처럼 이루어지며, 현재 값은 과거값에 ρ를 곱하고, 과거에 나오는 gradient를 누적해서 계산한다. 여기서 ρ는 1보다 작은 값이기 때문에 연속적으로 곱할 경우 계속 작아진다. 즉, 이 과정에서 먼 과거의 값의 영향이 작아진다.
momentum을 사용할 경우, gradient가 0인 지점이 발생하더라도, 계속 학습을 진행할 수 있게 도와준다.
Nesterov Momentum
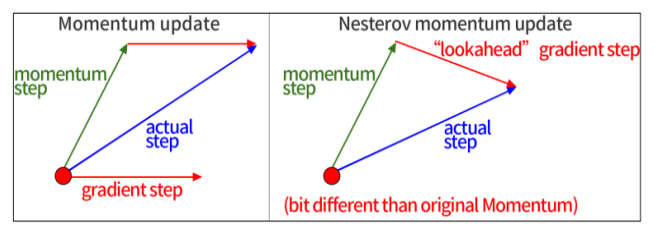
nesterov momentum은 gradient를 먼저 평가하고 파라미터를 업데이트 하는 방식이며, 이를
lookahead gradient step이라고 칭한다.
기존 방식의 경우 벡터의 합으로 계산 했지만, 본 방식의 경우 momentum step으로 이동 후
lookahead gradient step을 계산한다.
AdaGrad
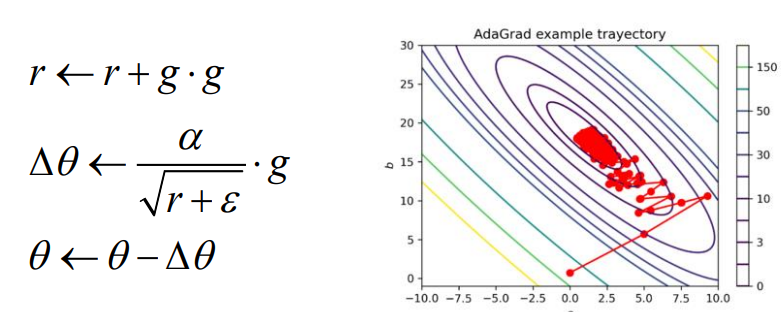
adagrad는 각 방향으로의 learning rate를 적응적으로 조절해 학습 효율을 올리는 방식이다.
gradient가 큰 경우 그 방향으로의 학습이 많이 진행되었음을 알 수 있고, learning rate를 조절해 적절한 값에 수렴할 수 있도록 한다.
식에서 처럼, r은 기존 r 값에 gradient의 제곱을 더하고, 학습과정에서 gradient 제곱 값이 누적되어 r은 계속 커진다. 두번째 수식의 r값을 보면, r이 커질 수록 θ가 작아짐을 알 수 있다.
만약, 학습과정이 진행이 더뎌 r값이 작으면 그 방향의 θ는 커져 수렴속도가 증가한다.
하지만, gradient 값이 누적됨에 따라 learning rate가 너무 작아질 경우 그 지점에서 학습이 진행되지 않을 수도 있다.
RMSProp
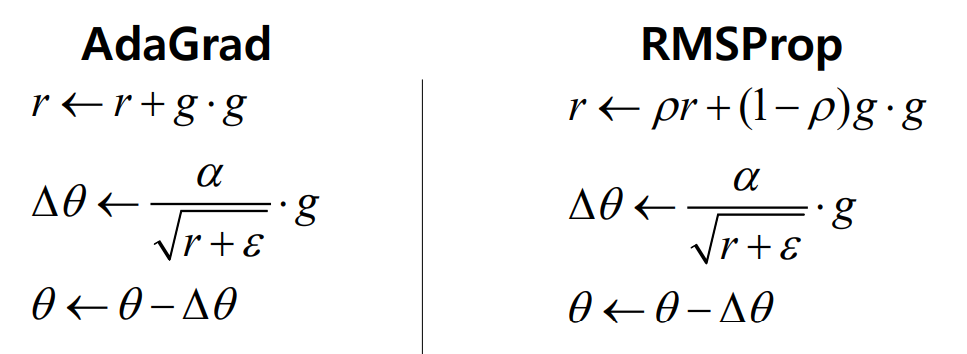
앞서 설명한 AdaGrad를 보완하여 나온 방법으로, r의 값이 극단적으로 커지거나 작아지는 문제를 보완했다.
r의 값을 과거 r만큼의 factor를 곱해 어느정도 조절하여 완충된 속도로 늘어나거나 줄어든다.
Adam (Adaptive Moment Estimation)
adam은 RMSProp + momentum의 구조를 가진 방식으로, 다음과 같은 프로세스를 따른다.
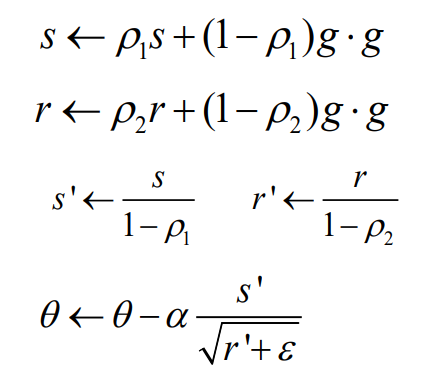
- 첫 번째
momentum계산 RMSProp momentum계산bias보정- 파라미터 업데이트
현존하는 gradient descent 기법 중 에서 가장 많이 사용된다.
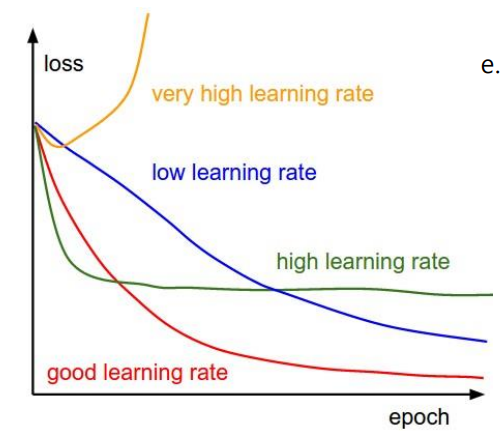
학습 전략도 고려하면 더 좋은 모델을 만들 수 있다.
그림에서와 같이 낮은 학습률과 높은 학습률을 비교하면, 낮은 학습률의 경우 속도는 느리지만, 더 낮은 error를 나타낸다. 높은 학습률의 경우 속도는 빠르지만, 조금 더 큰 error를 나타낸다.
이를 융합하여 수렴단계마다 적응적으로 학습률을 조정하는 방식을 통해 속도와 error 둘 다 잡을 수 있다.
Avoid Overfitting
overfitting은, 모델이 지나치게 복잡하여 학습 파라미터의 숫자가 증가해 제한된 학습 샘플에 너무 과하게 학습되는 것을 말한다.
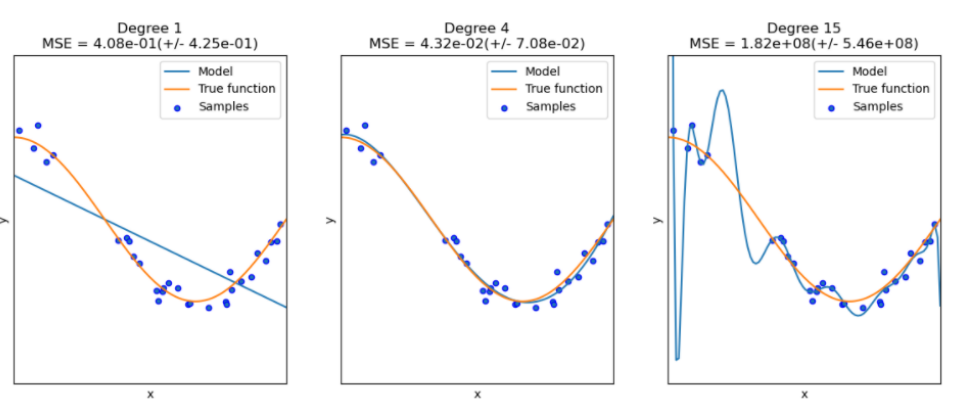
그림 속 주황색 선이 Target Function이고, 초록샌 선이 모델이다. 가운데에 있는 그림이 가장 적합하게 학습을 잘한 경우이며, 오른쪽 그림의 경우 모든 데이터 샘플에 fitting 되어 overfitting이 발생함을 알 수 있다.
이와 같은 경우 error는 적지만, 실질적인 Target Function을 따르기는 쉽지 않다.
입력변수가 많을 경우에도 파라미터의 수가 증가하는 문제로 인해 overfitting이 발생하기 쉽다.
그럴 경우, 모델의 파라미터 개수를 줄여 복잡도를 줄이는 방식을 택한다.
Regualization
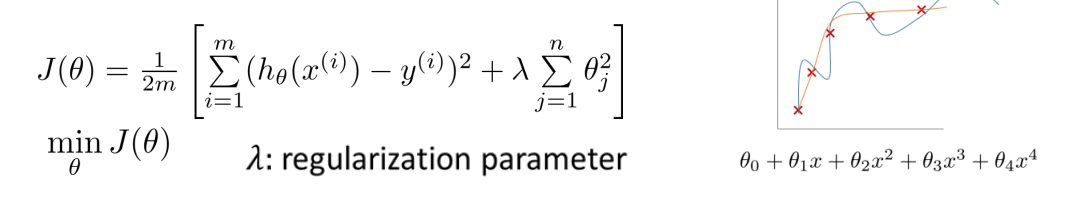
regualization은 학습 과정에서 모델의 복잡도에 대해 패널티를 주어 모델이 overfitting 되지 않도록 한다.
이로 인해, 모델은 적은 수의 파라미터를 사용해 주어진 문제의 샘플들을 fitting 하고자 할 것이며 overfitting을 예방한다.
수식에서 θ_J가 커지면 error의 값이 늘어나는 식의 λ를 사용해 모델에게 패널티를 부여한다.