해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다
오늘은, 모델의 출력이 이산 값을 가지는 Classification을 알아본다.
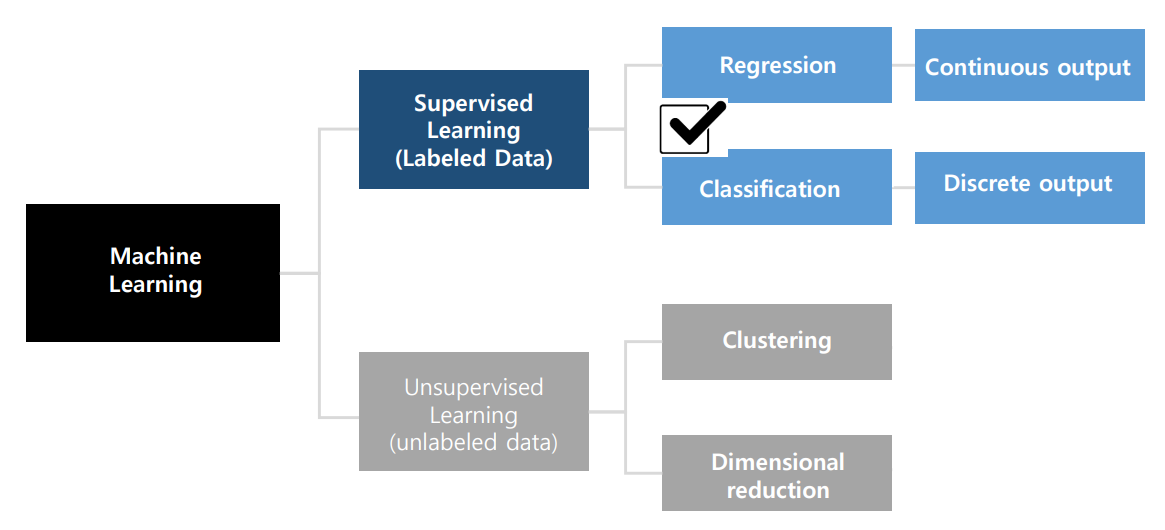
Classification은 입력의 category를 결정하고 분류하기 위해 데이터셋에서 입력과 정답으로 구성된 label이 있는 데이터 쌍을 사용한다.
Linear Classification
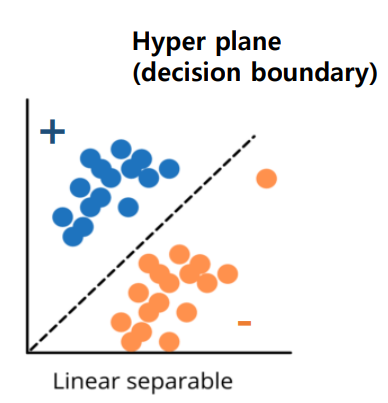
linear classification은 hyper plane을 구해 데이터셋에 있는 Positive Sample과 Negative Sample을 linear combination을 기준으로 구분하는 작업이다.
그림 속 hyper plane은 두 그룹을 분류하는 decision boundary로 사용하며, h(x) = 0으로 나타낸다.
positive sample은 h(x) > 0의 그룹이고 negative sample은 h(x) < 0의 그룹이다.

수식 속 w는 모델의 파라미터이며, x는 입력값 feature다.
Multi-Class Classification
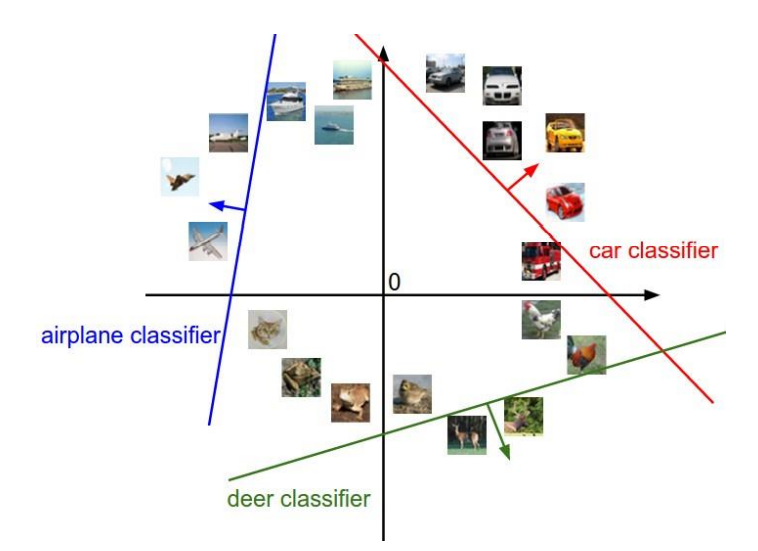
multi-class classification은 하나의 hyper plane을 사용하는 일반적인 classification과 달리 입력신호공간에서 여러 개의 hyper plane을 사용해 classification을 수행한다.
Linear Classification Framework
linear classification은 decision boundary의 정확한 추정을 통해 주어진 입력에 대해 출력의 분류를 수행하며 학습 데이터의 입력과 출력상으로 linear boundary를 학습하고, 그로부터 입력 feature가
hyper plane으로부터 어느 위치에 있는지 결정한다.
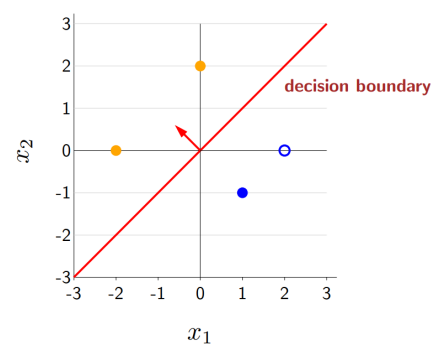
classification을 진행할 때 고려해야할 것은 다음과 같다.
- 어떤
predictor를 이용할 것인가? ->h(x) = sign(w^Tx) - 어떤
loss function을 이용할 것인가? ->Zero-one loss,Hinge loss,Cross-entropy loss - 어떤 기법을 통해
parameter optimization을 진행할 것인가? ->Gradient descent algorithm
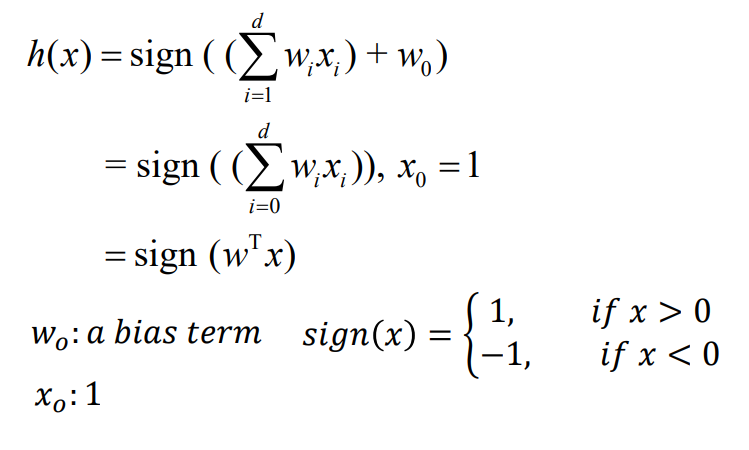
위의 수식에서 w_0는 bias, offset을 나타내며, 입력변수 * 파라미터는 score 값으로 생각한다. 여기서 입력변수와 파라미터는 d+1 dimentional vector다.
sign(x)는 x의 값에 따라 x가 0보다 클 경우 1의 값을, 작을 경우 -1의 값을 나타낸다.
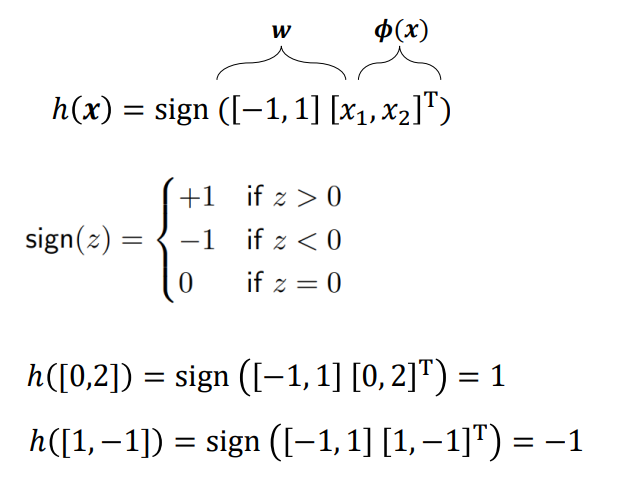
입력 score W^Tx의 값은 좌표상에서 함수h(x)로부터 해당 점까지의 거리를 뜻하며 값이 커질 수록 거리도 늘어난다.
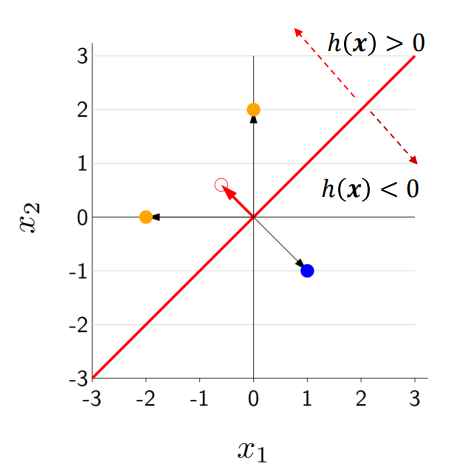
2개 점의 score 값이 동일한 경우 좌표상 각 점들과 h(x)와의 거리는 똑같다.
Hypothesis class
classification은 w값에 따라 decision bounadry의 형상도 달라진다.
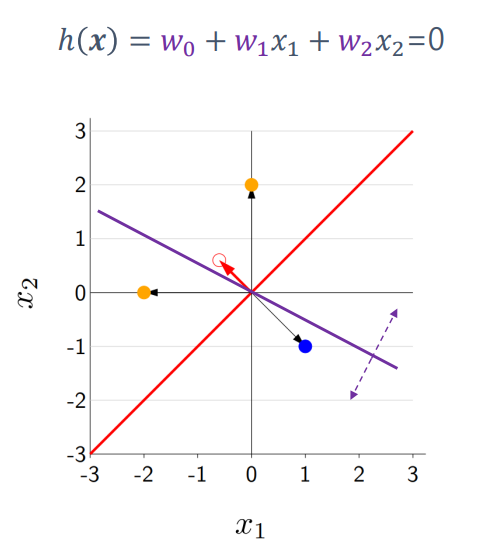
빨간색 hyper plane은 [-1, 1] 의 형태
보라색 hyper plane은 [0.5, 1]의 형태다.
classification에서의 문제는 parameter w를 학습하는 것이다.
학습을 진행하려면 error 값이 필요한데, classification에서 error를 어떻게 판단할까?
그에 대한 방법으로 zero-one loss가 있다.
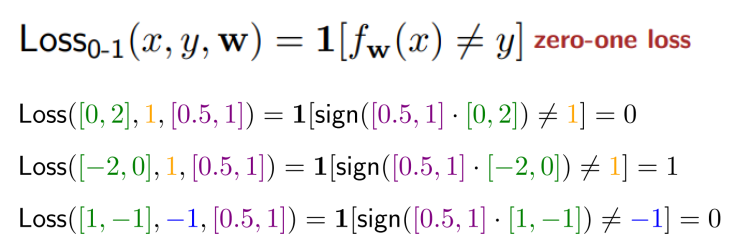
해당 방법은 내부의 로직을 판별해 맞으면 0, 틀리면 1의 결과를 출력한다.
앞전에 설명했던 Sign(x) 함수를 사용하여 내부 로직을 판별한 결과는 위와 같다.
Score and Margin
score 값은 결정과정에서 model이 얼마나 confident한지 측정가능한 지표다.
margin 값은 score 값에 y를 곱해 계산하여, 모델이 얼마나 정확한지 측정가능한 지표다.
이 둘의 관계를 이용해 모델의 학습이 잘 되어가고 있는지를 확인할 수 있다.
-
score +y = 1인 경우, 모델이 정답을 맞추었다고 생각하여margin이 양의 값으로 증가 -
score -y = -1인 경우, 위와 같음 -
score +y = -1인 경우, 모델이 정답을 맞추지 못했다고 생각하여margin이 음의 값으로 감소 -
score -y = 1인 경우 위와 같음
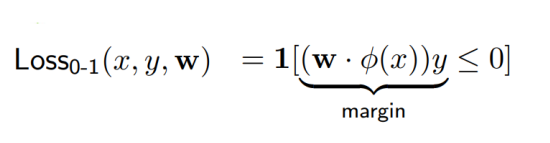
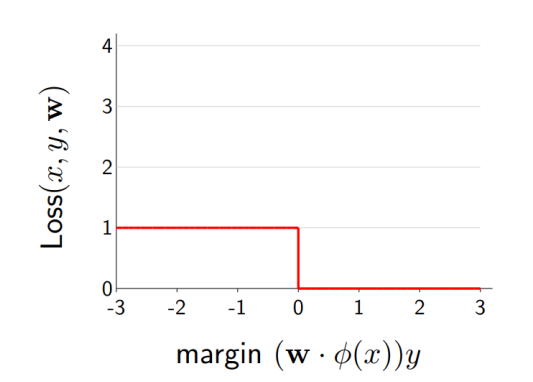
zero-one loss의 경우 gradient가 0이 되는 경우가 발생해 학습을 제대로 진행할 수 없다
Hinge loss
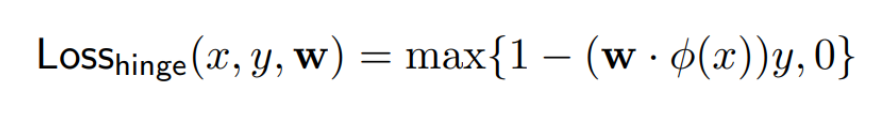
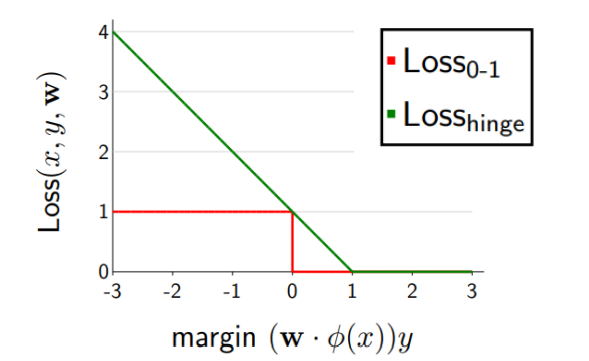
hinge loss의 경우 [1-margin, 0] 중 큰 값을 선택하는 loss function으로, 모델이 정답을 잘 맞추는 경우에는 margin이 큰 양의 값을 가져 [1-margin, 0]에서 1-margin이 음의 값을 가질 것이므로 loss는 0이 된다. 반대로 정답을 잘 못맞출 경우에는 1-margin의 값이 양의 값을 가져 loss가 발생하게 된다.
즉, margin이 1보다 작으면 error가 발생하고, 1보다 클 경우 error가 없는 것으로 여긴다.
Cross-Entropy Loss
cross-entropy loss는 classification 모델 학습에 가장 많이 사용하는 loss function이다.
p와 q의 값이 유사한지에따라 error의 정도가 바뀌는 특징을 가진다. 유사할 경우 loss가 감소하고, 유사하지 않을 경우 loss가 증가한다.
classification에서 fitting을 하고자하는 label은 1아니면 0인 값이 되는데,cross-entropy 방식은 확률 값이고 모델의 score 값은 실수 값이므로 해당 실수를 확률 값으로 매핑하는 확률함수가 필요하다. 이때 사용되는 함수가 바로 sigmoid 함수다.
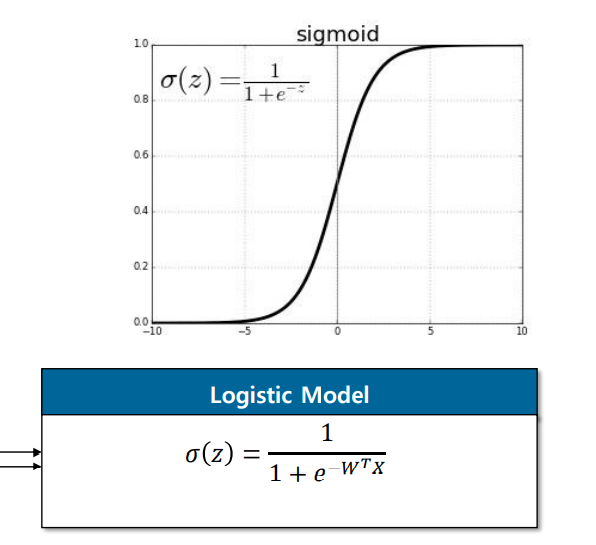
sigmoid 함수의 경우 0일 때 0.5의 값을, 양의 값으로 다다르면 1에 가까워지고 음의 값으로 다다르면 -1에 가까워지는 특징의 함수다. 즉, score 값을 sigmoid 함수에 넣어 0~1 사이로 매핑한다.
이런 형태를 logistic model이라고 한다.
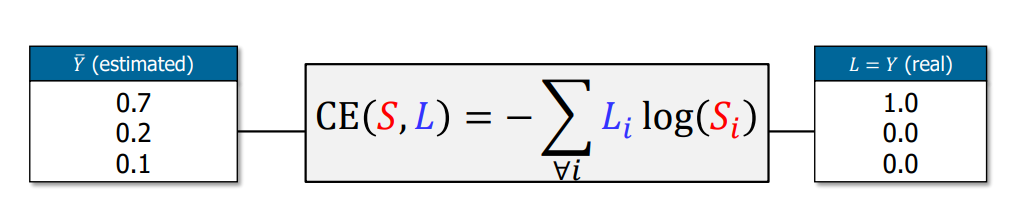
실제 classification은 위 그림과 같이 수행될 것이다. 양 측의 총합은 1로 확률 값을 나타내며 왼쪽 y hat의 경우 예측한 값으로, 모델의 출력값이다. 오른쪽 Y는 class에 따른 정답이므로, 모델의 예측에 error가 발생함을 알 수 있다.
이 때 모델이 loss값을 이용해 잘 학습한다면, 추후에 오른쪽 Y의 값처럼 [1.0, 0.0, 0.0]에 점점 가까워질 것이다.
만약 예측한 값이 [1.0, 0.0, 0.0] 이면, error는 0에 수렴한다.
Training a Linear Classifier
linear classifier의 학습 단계는 다음과 같다.
weight을 initialization 한다.gradient를 계산한다.- 첫 움직임의 방향을 설정한다.
weight을 업데이트한다.- 완료될 때 까지 반복한다.
Multiclass Classification - One vs All
특정 classification 모델의 경우 multiclass classification 문제에서 class-id를 출력하는 경우도 있지만, 보통의 경우 binary classification 문제를 multiclass classification으로 확장한 경우가 많다.
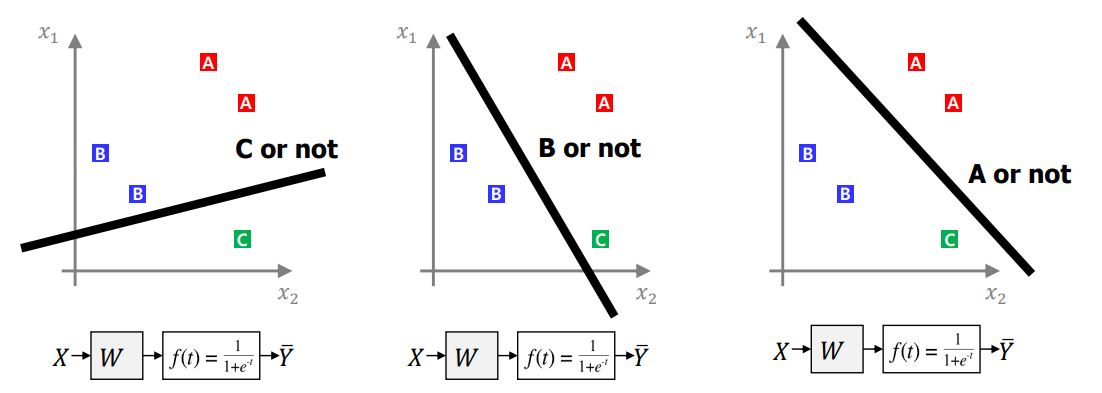
이는 즉, 그림에서와 같이 C 거나 아니거나, B거나 아니거나 A거나 아니거나 와 같은 형태로 진행된다.
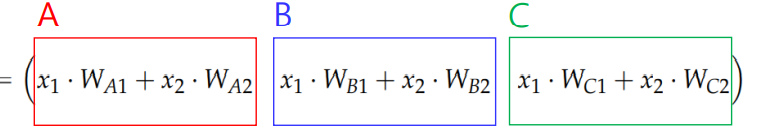
수식으로부터 score 값을 획득하여, sigmoid 함수를 사용하면 확률 값으로 값을 mapping해
multiclass classification을 완료한다.

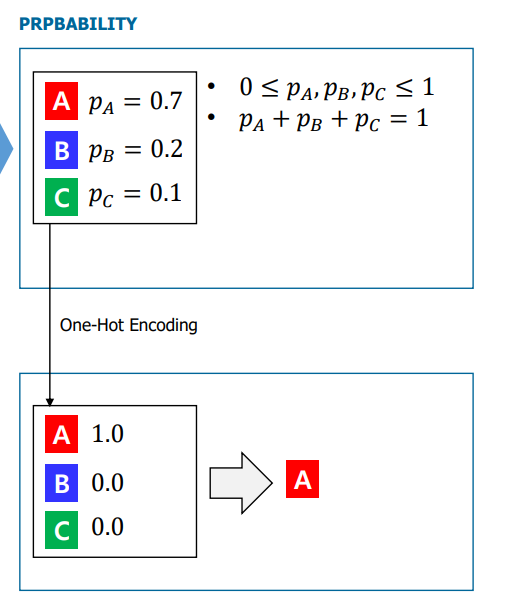
One-Hot Encoding
one-hot encoding은 2개의 서로 다른 표 사이의 거리를 가깝게 하여 학습하게끔 하는 방식으로, label을 지정할 때 사용한다.
그림에서와 같이 one-hot encoding 된 label의 값과 sigmoid 모델이 출력하는 확률 값을 서로 비교하여 loss function을 통해 error를 계산하여 학습을 진행한다.
Advantage of Linear Classification
- 모델의 구조가 단순하고 간단하여 구현 및 테스트가 쉽다.
- 해석가능성이 증가하여
decision boundary등의 작업이 수월하다.
-> 요소별로 요소가 1단위 씩 증가할 때마다 전체score값이 어떻게 변하는지를 추정함으로써 해석 가능성을 제공한다.