해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다.
이번 시간에는 대표적인 Classification 모델 몇가지와 관련 지식을 알아본다.
linear classification의 경우 hyper plane을 구성하는 모델의 파라미터가 w일때, hyper plane의 normal한 방향으로 hyperparameter w vector를 구성한다.
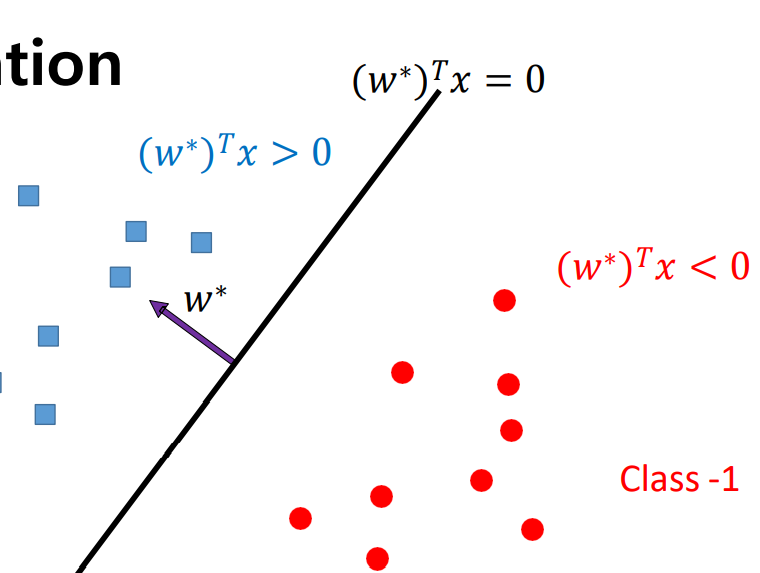
하지만 위와 같은 상황에서 서로 다른 hyper plane을 그렸을 떄 그림 속의 데이터 샘플들에 대해서는 비슷한 loss를 제공하게 될 것이지만, 실제 세상의 데이터 샘플에서는 보이지 않는 다양한 샘플이 존재하여 서로 다른 hyper plane들은 각기각색의 성능을 제공할 수 있다.
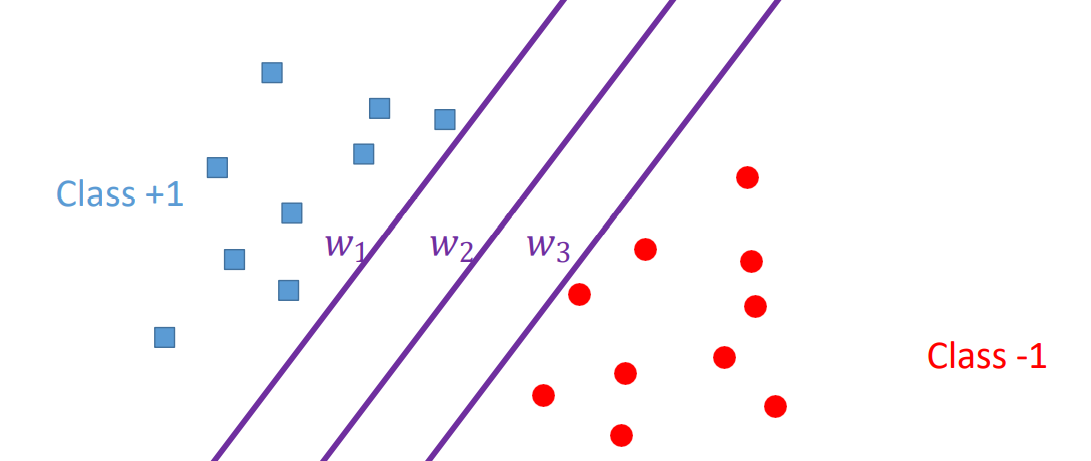
위 그림의 W1 W2 W3 중 가장 적절한 hyper plane은 W2다.
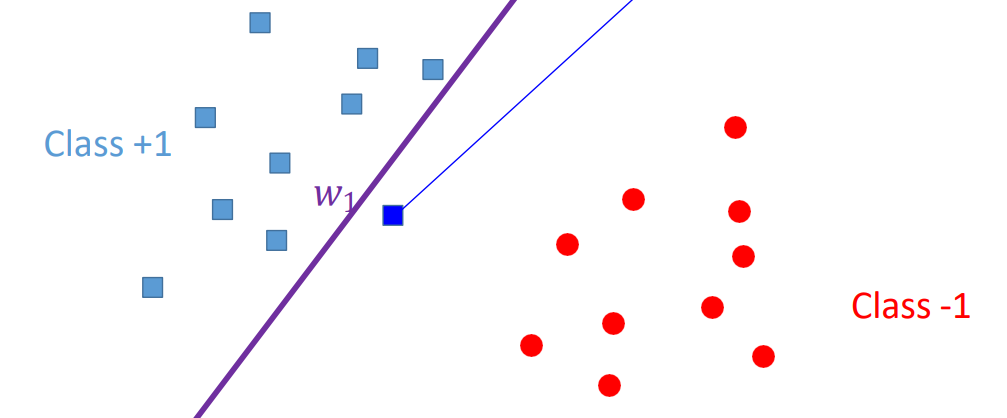
W1의 경우 잘 분류했지만, 위 그림처럼 새로운 데이터 샘플이 뒤쪽에 나타나버린 경우 오류가 발생하게 된다.
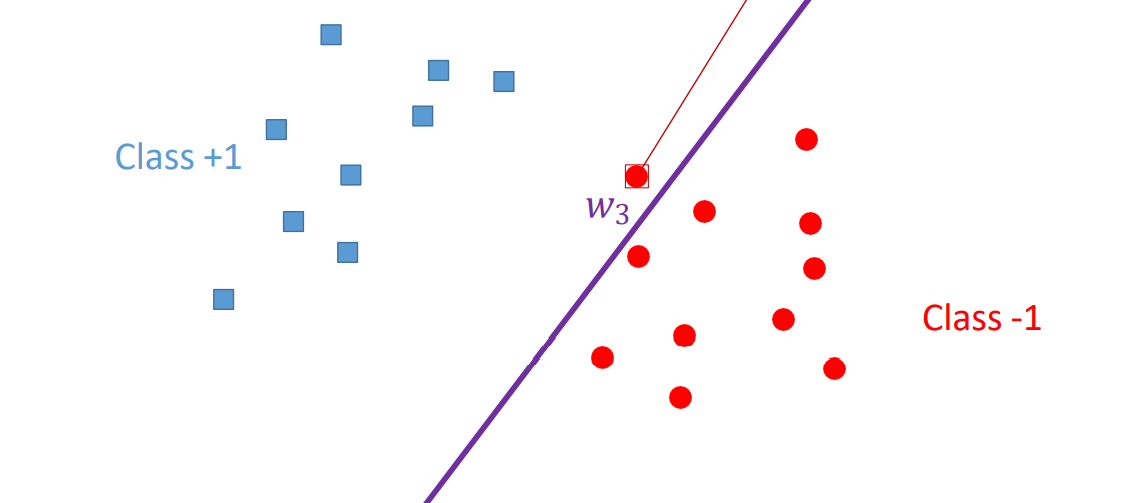
W3의 경우도 마찬가지로, 잘 분류했지만 새로운 데이터 샘플이 위 그림처럼 존재하는 경우 오류가 발생한다.
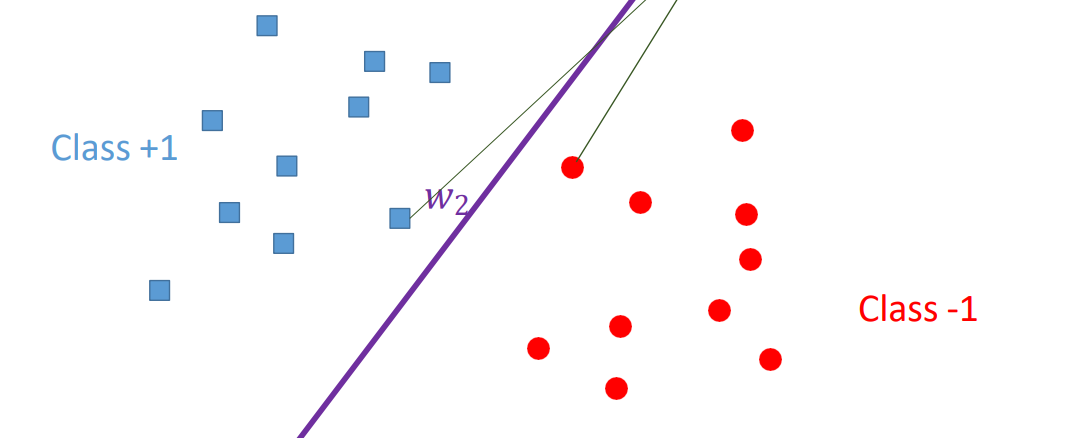
하지만 W2의 경우 적절한 중간 공간에 배치되어 새로운 데이터 샘플이 만들어져도, 잘 분류하는 것을 알 수 있다.
즉, hyper plane의 가장 적절한 위치는 positive sample와 negative sample의 중간위치다.
margin
Support Vector Machine의 핵심 아이디어는 hyper plane을 결정하는 margin이다.
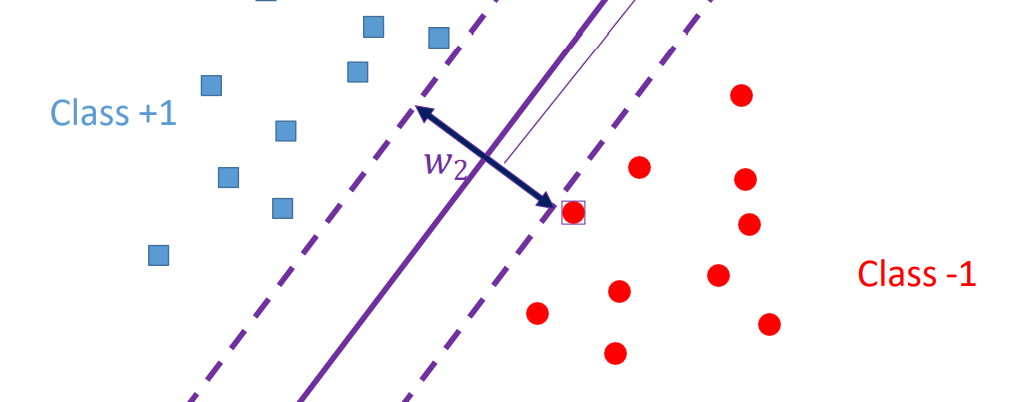
위 그림과 같이 가장 가까운 positive sample과 negative sample을 기준으로 최대 margin 폭을 갖는 최적화 방법을 생각한다.
Support Vector Machine : SVM
svm은 support vector로 칭하는 포인트 간의 거리를 최대화 하는 최적화 전략이다.
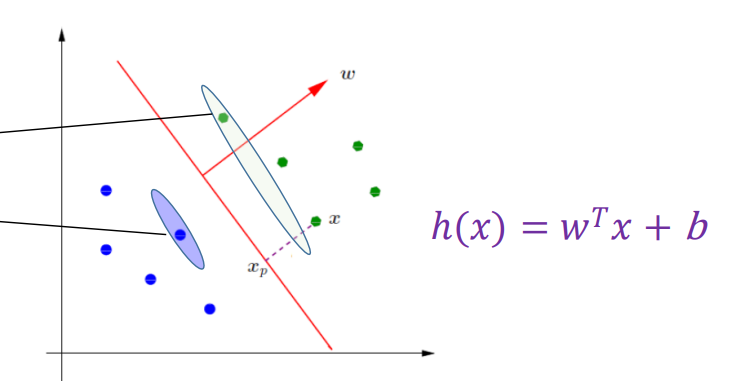
support vector는 positive sample과 negative sample 중 hyper plane과의 거리가 더 짧은 sample을 의미한다.
해당 포인트는 모델 classification의 성능을 좌지우지하는 민감한 데이터 포인트다.
이런 특성으로 인해 outlier가 발생해도 견고하게 잘 대처할 수 있다.
margin은 support vector와 h(x)와의 거리를 2배하여 구한다.
수식으로 나타낼 경우 다음과 같다.
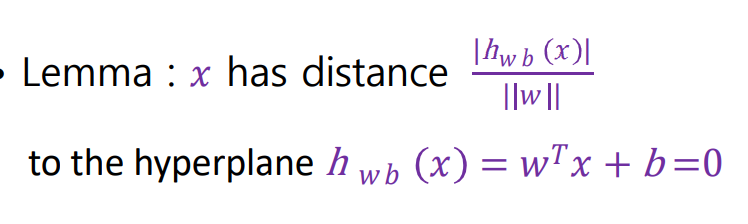
Optimization
떨어져 있는 support vector 간 거리를 최소화하기 위해 svm에서 다양한 최적화 방식을 이용한다.
Hard margin SVM:linear separability를 가정하여h(x)와support vector사이의 영역에는 어떠한 샘플도 존재하지 않을 것으로 생각Soft margin SVM: 어느정도의error는 용인하는 방식의 최적화 방법Nonlinear transform & Kernel trick:SVM이linear separable한hyper plane을 이용해 수행하기 때문에linear한 경우에만 사용할 수 있다는 단점을 극복하기 위해 만들어졌다. 이를 이용할 경우 아래의 그림과 같이 2차원의 샘플을 보다 고차원의 샘플로 맵핑하는 함수를 이용해 수행한다.
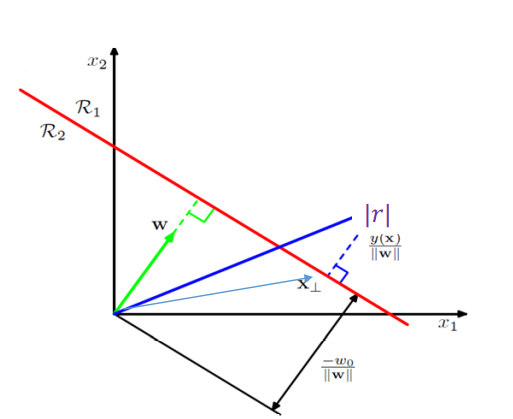
hard-margin linear SVM에서는, h(x) = 0 hyper plane을 두고 margin을 다음과 같이 계산한다.
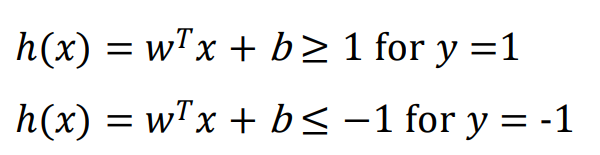
positive sample을 지나는 h(x)를 위의 수식, negative sample을 지나는 h(x)를 아래 수식으로 나타낸다.
SVM에서의 모든 샘플은 다음과 같이 나타낸다.
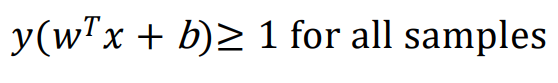
margin에 대한 식을 정리하면, 아래와 같이 정리된다.

즉, 결론적인 SVM에서 풀고자하는 문제는 ||w||를 최소화하여 margin을 극대화하는 것이다. 이를 SVM Primal Problem이라고 여긴다.
nonlinearly separable; Kernel Trick
kernel fucntion은 linearly separable하지 않은 데이터 샘플이 있다고 할 때, 차수를 높여 linear separable 하게 만드는 과정에 사용한다.
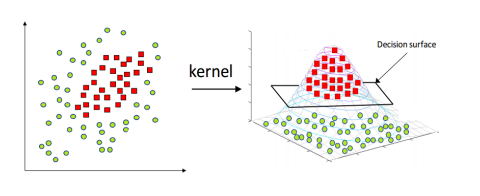
아래의 그림과 같이 2차원의 좌표상에서 표현되는 정보를 kernel trick 과정을 통해 사과와 체리를 정확하게 구분하는 decision surface를 정의한다.
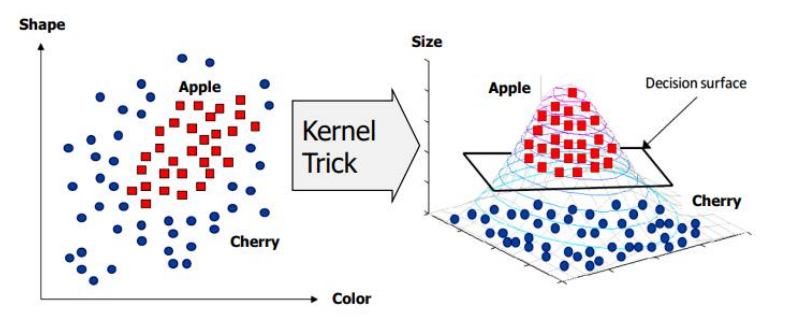
kernel에서 주로 사용하는 기법들은 다음과 같다.
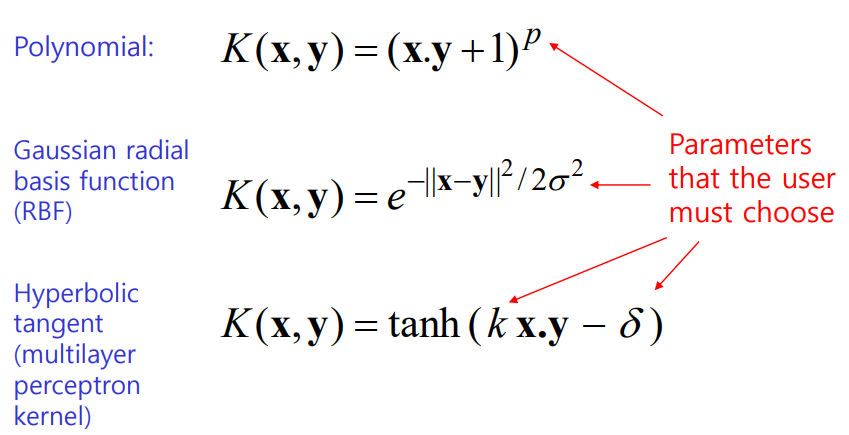
이들은 각각 고유한 파라미터가 있어 사용자가 선택해야하며, 선택한 값에 의해 서로 다른 형식의 plane으로 매핑하게 된다.
Artificial Nerual Network (ANN)
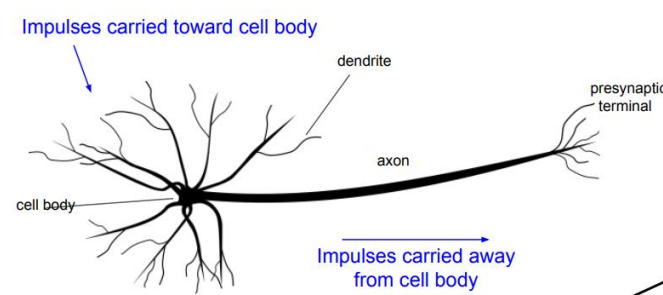
Deep Nurual Network의 기본 개념인 ANN은 non-linear classification model이다. 이는 인간의 뇌신경망을 모사한 Perceptron 개념이다. 우리 뇌에서 일어나는 작업과 유사하게 수행된다.
먼저 이전의 노드 x0 등을 통해 각각의 고유 파라미터 W0 W1 W2를 곱해 linear combination으로 만든 score 값을 이용한다.
Activation Functon은 linear combination으로 만든 score 값을 입력으로 삼아 sigmoid와 같은 함수를 통해 non-linear 관계로 매핑한다.
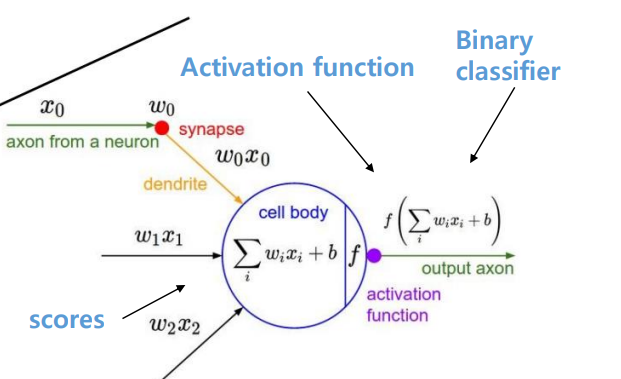
Activation Functions
sigmoid도 activation function의 한 종류지만, Z 값이 크거나 작을 경우 gradient가 너무 작아 학습을 진행함에 따라 학습량이 계속 작아지는 문제가 있다.
이를 보완하기 위해 만든 activation function으로 ReLU, Leaky ReLU, tanh 등이 있다.
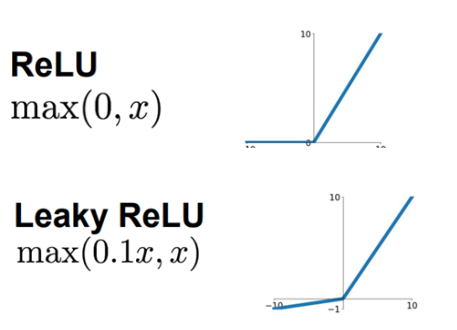
해당 함수들은 미분을 하더라도 gradient가 1로 수렴하게끔 설계되어 학습이 멈추지 않는다.
Deep Nerual Network
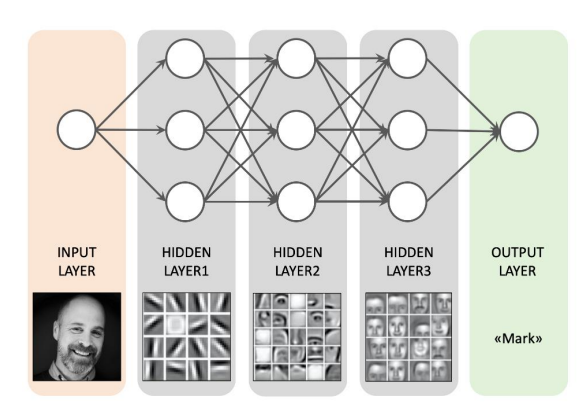
DNN의 자세한 연산과정을 알 수 없지만, 각각의 계층을 따라서 학습하게 되는 feature의 어떤 형태가 달라진다고 알려져 있으며, non-linear 함수들이 계층적으로 쌓여감에 따라 signal space에서 복잡한 신호들의 패턴을 조금 더 정확하게 분류할 수 있다.
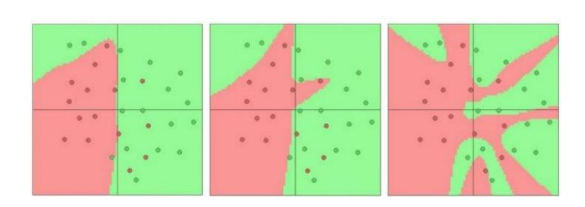
위 그림처럼, 정확한 분류를 위한 linear plane의 구성이 어려운 경우, 여러 개의 계층으로 이루어진 DNN에서 계층을 통과하며 복잡한 모델을 구성해 잘 분류한다.
Multilayer Perceptron
linear plane을 통해서 해결할 수 없는 대표적인 문제로, XOR 문제가 있다.
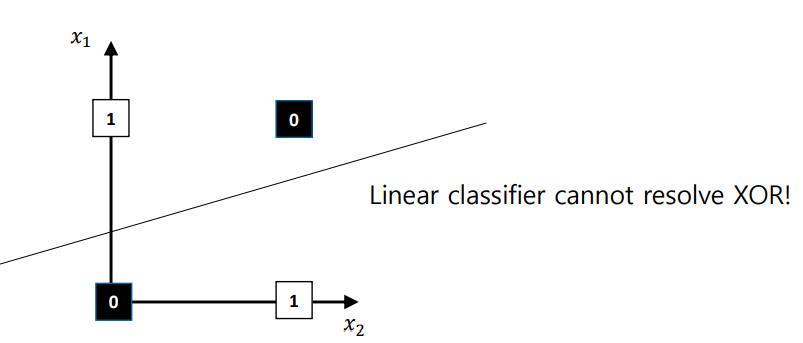
어떤 방향으로 plane을 그려도 0과 1을 정확히 구별할 수 없다.
하지만, multilayer perceptron을 이용하면 XOR 문제도 간단히 해결할 수 있다.
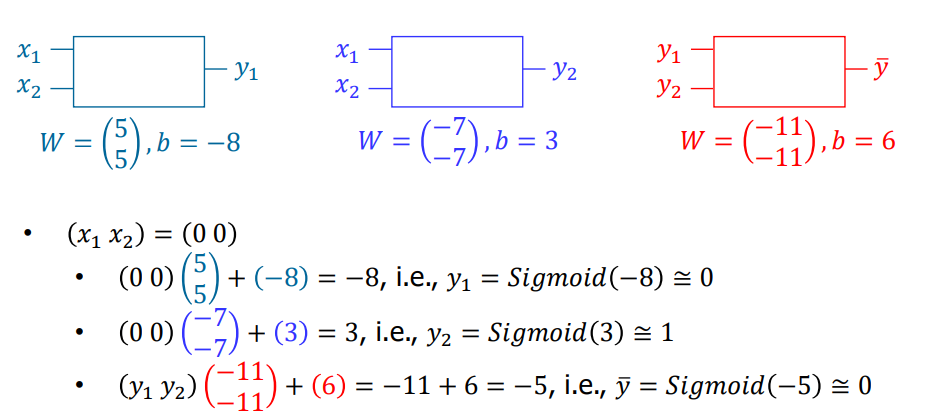
위 그림과 같이, 단순한 2계층으로 구성된 함수가 있다.
y1 y2를 구하고, 이를 이용해 최종 답인 y-를 내놓는다.
사전에 정의된 W와 입력 값 X1 X2를 곱해 각 Y의 출력을 생성하고 sigmoid 함수를 통해 0이나 1에 매핑한다.
sigmoid를 통해 도출된 Y1 Y2를 정의된 W와 곱해 출력을 생성하고, 다시 sigmoid 함수를 통해 최종 결과를 도출한다.
위와 같은 과정을 입력 (0, 0) (0, 1), (1, 0), (1, 1)에 대해 수행하면, XOR 문제가 해결된다.
결론적으로 nerual network는 linear classification 문제에서 수행할 수 없는 non-linear한 문제들을 잘 해결하며, 고차원의 신호나 이미지와 데이터에 더 정확하게 동작한다.
Gradient Vanishing Problem
모델학습 과정에서 학습 파라미터의 학습은 Chain rule을 통해 진행하는데, DNN의 계층이 커질수록 Gradient가 줄게되어 깊은 레이어에서 학습효과가 없어지는 현상이 발생한다.

해당 문제는 Back Propagation 과정, Pre-training, fine-tuning 등으로 극복한다.
Supervised Learning의 기본원리는, 입력을 넣고 결과 값 쌍으로부터 에러를 추정하여 해당 에러를 최소화하는 과정으로 최적화를 통해 모델 피팅을 수행하는 것이다.