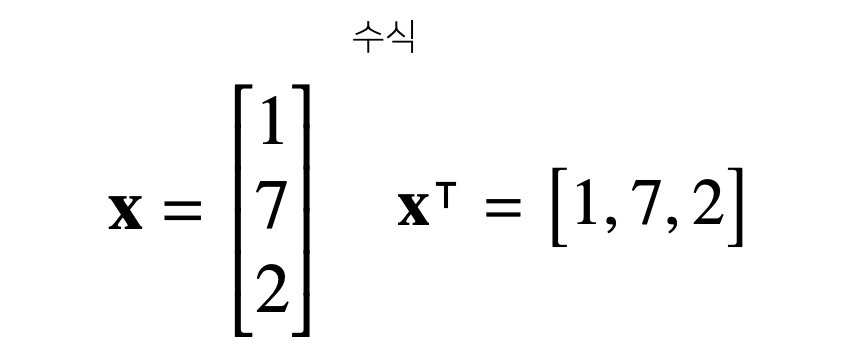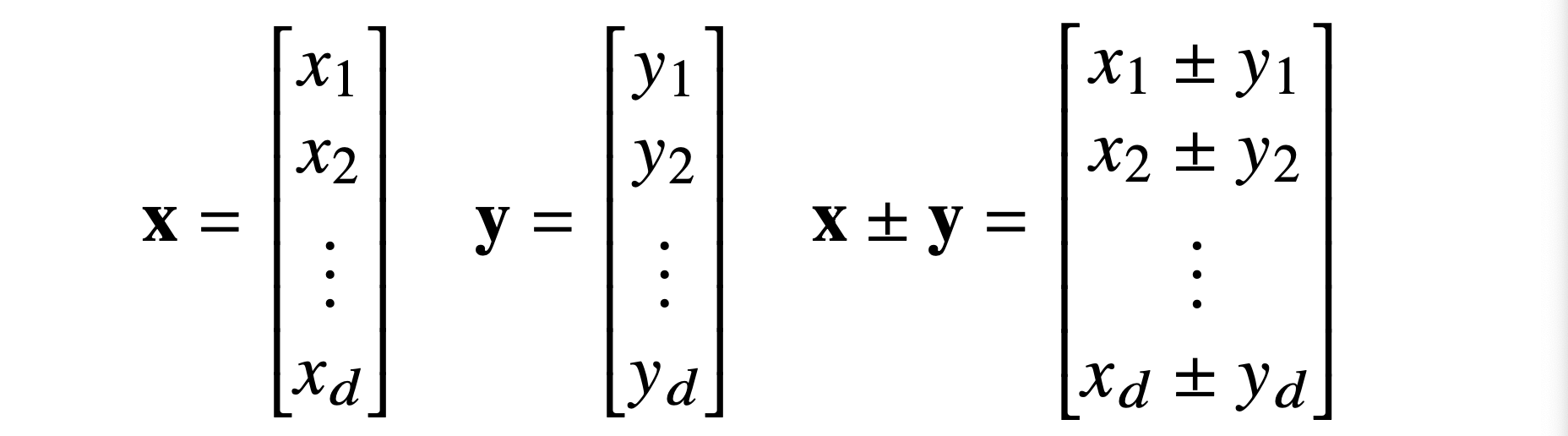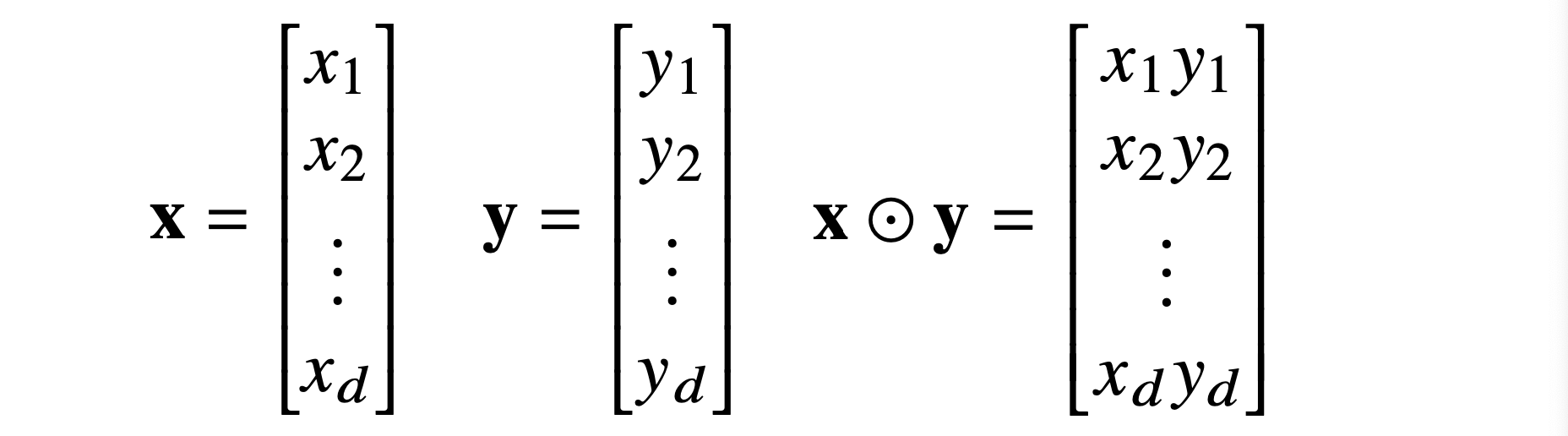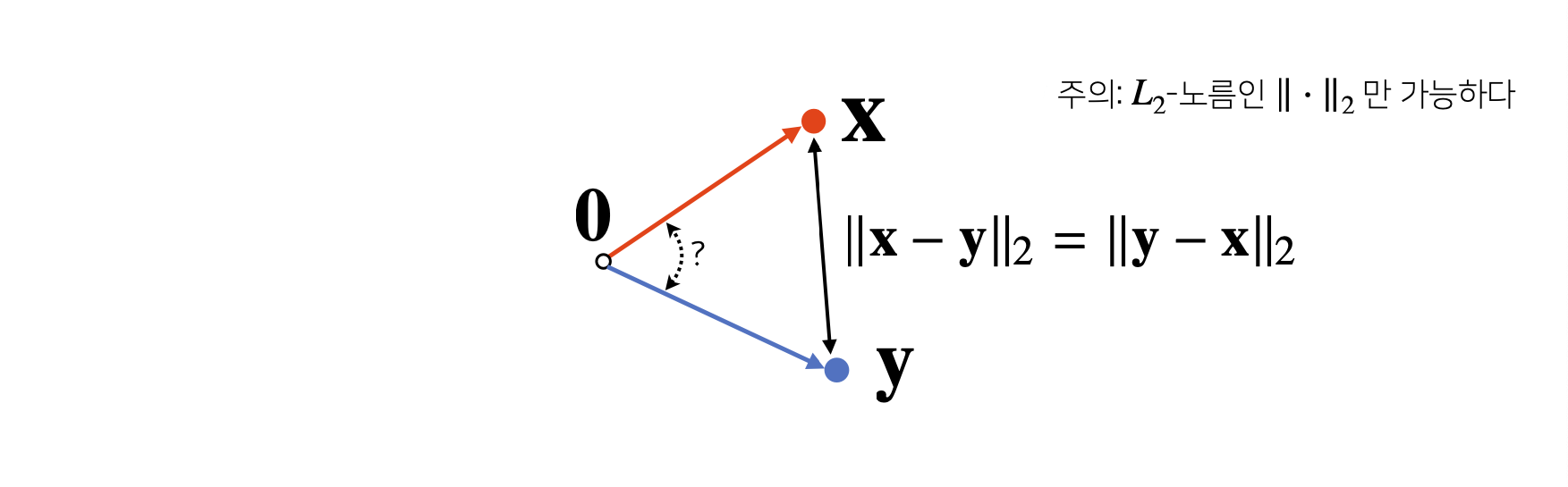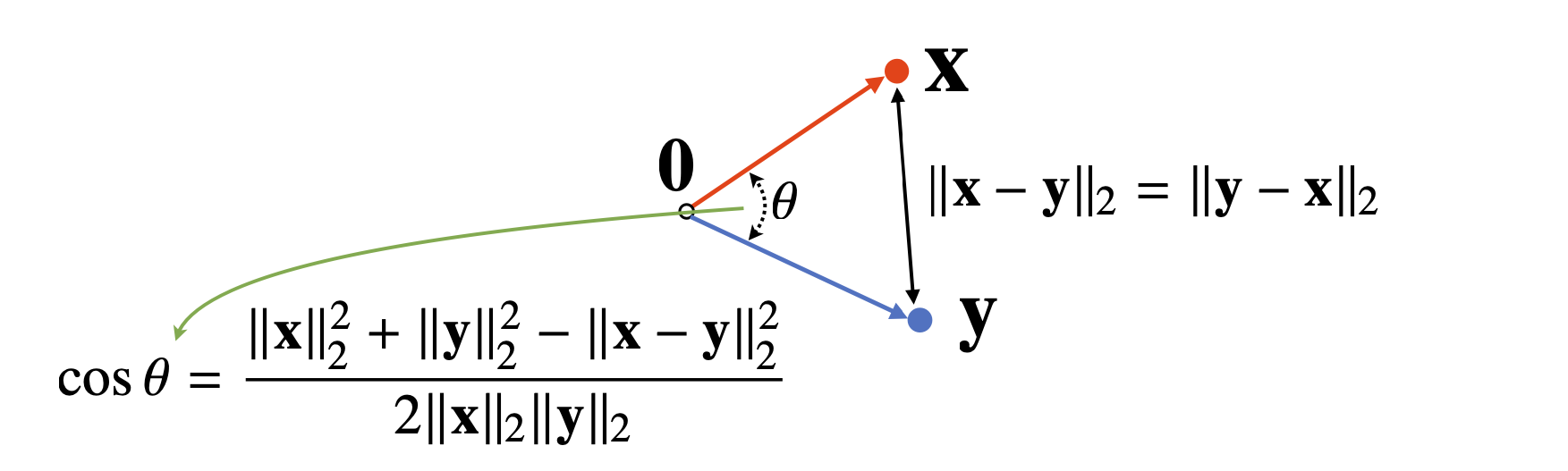Lec8: Mathematics for Artificial Intelligence_Vector

01_Vector

1) Vector?

• Vector : 숫자를 원소로 가지는 List 또는 Array
• Column Vector, Row Vector
  

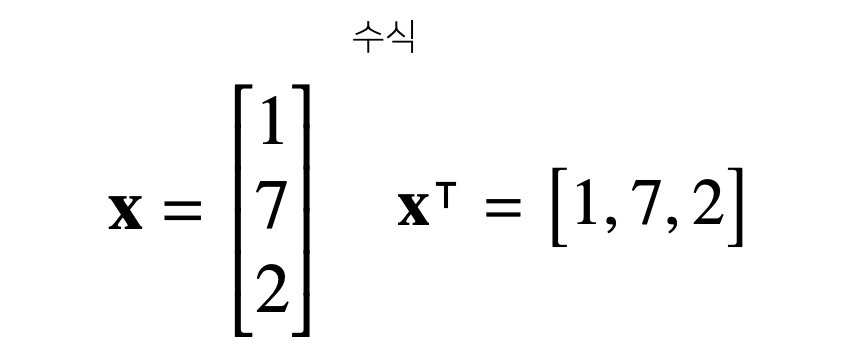
x = [1, 7, 2]
x = np.array([1, 7, 2])

• Vector는 공간에서 한 점을 나타낸다.
  
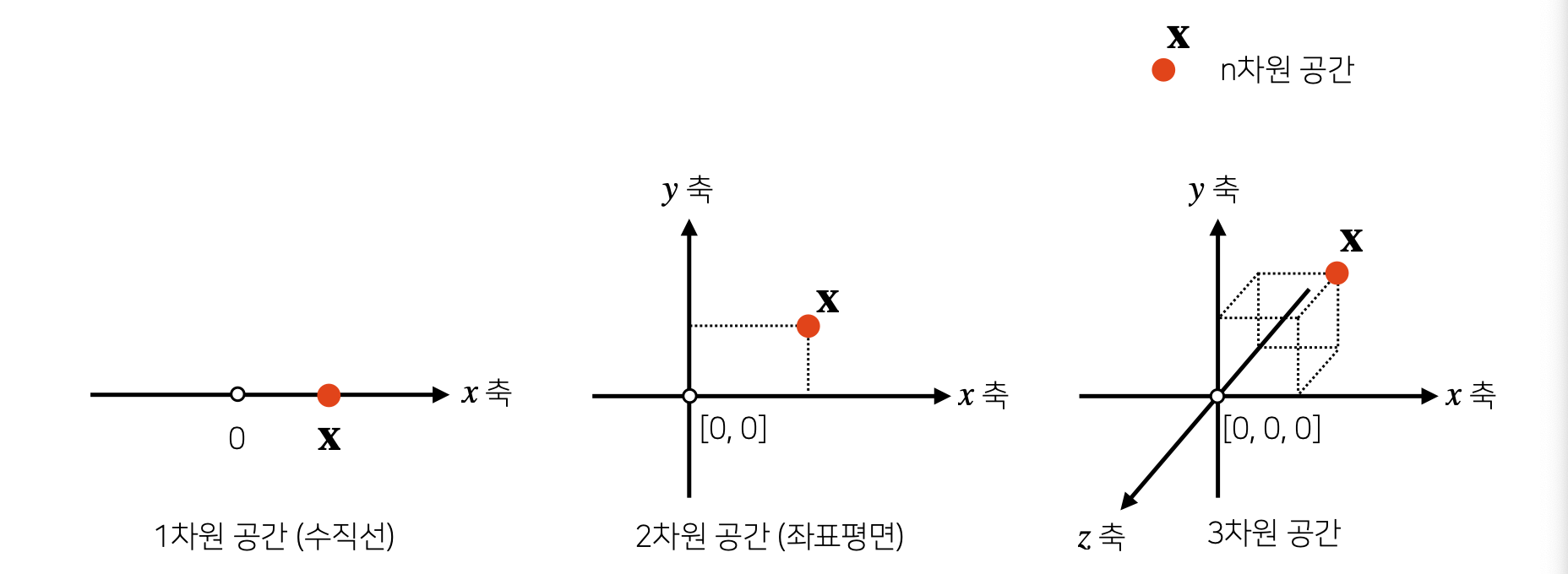
• Vector는 원점으로부터 상대적 위치를 표현한다.
  
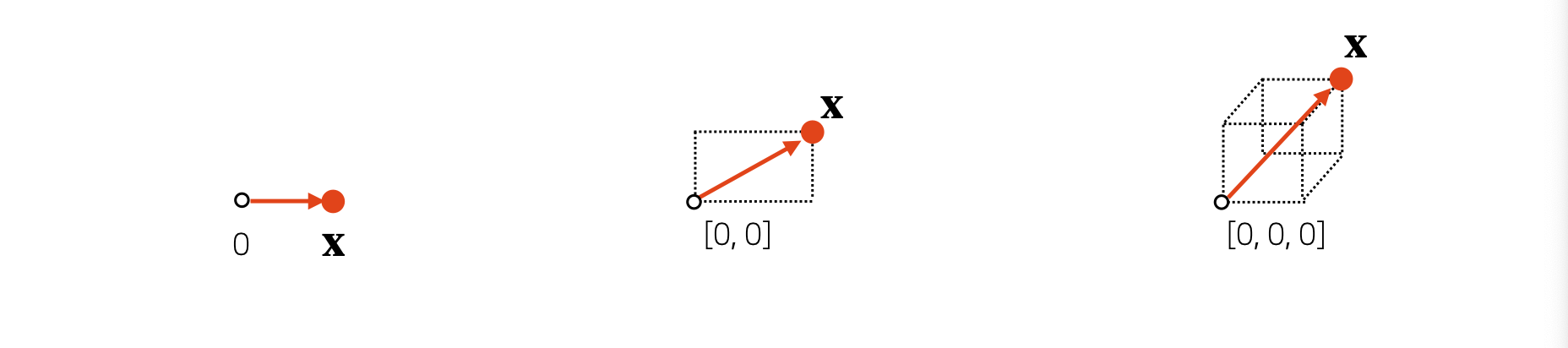
• Vector에 숫자를 곱해주면 길이만 변한다.
  
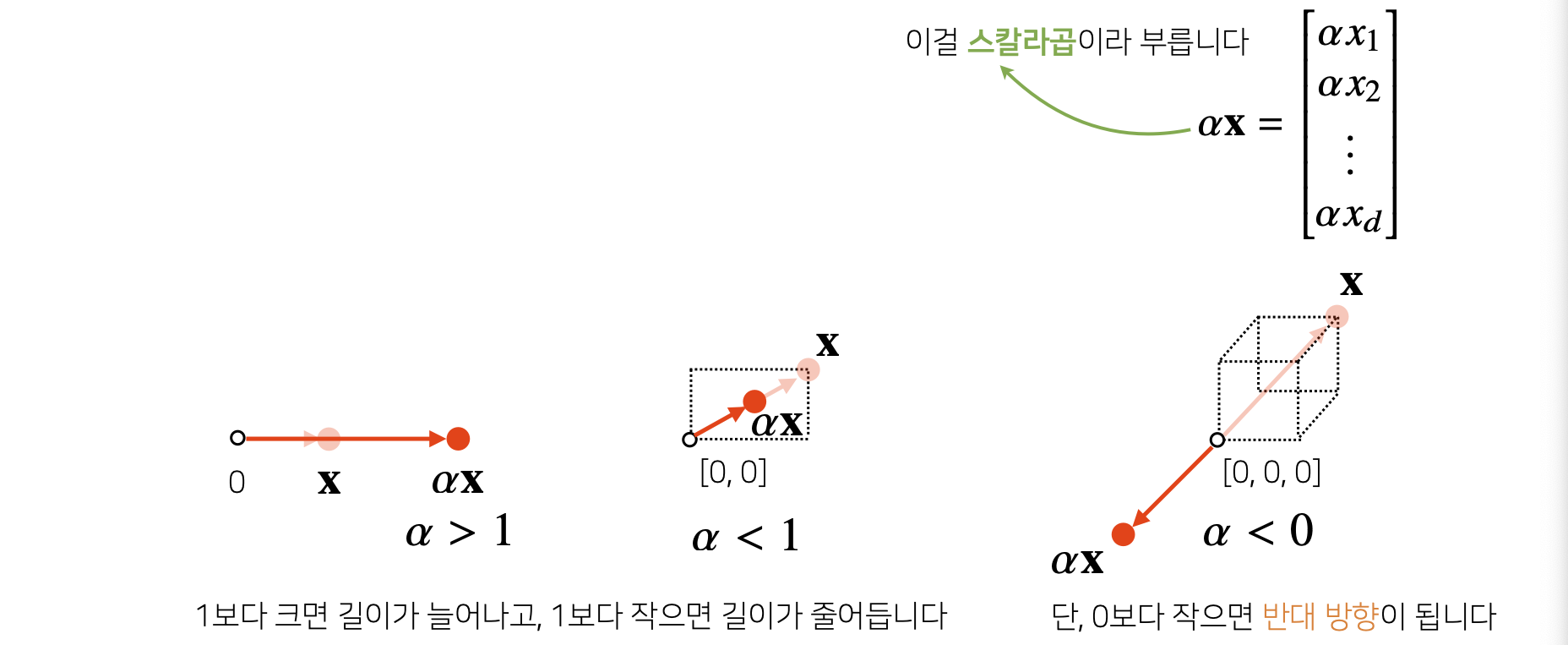
• Vector끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
  
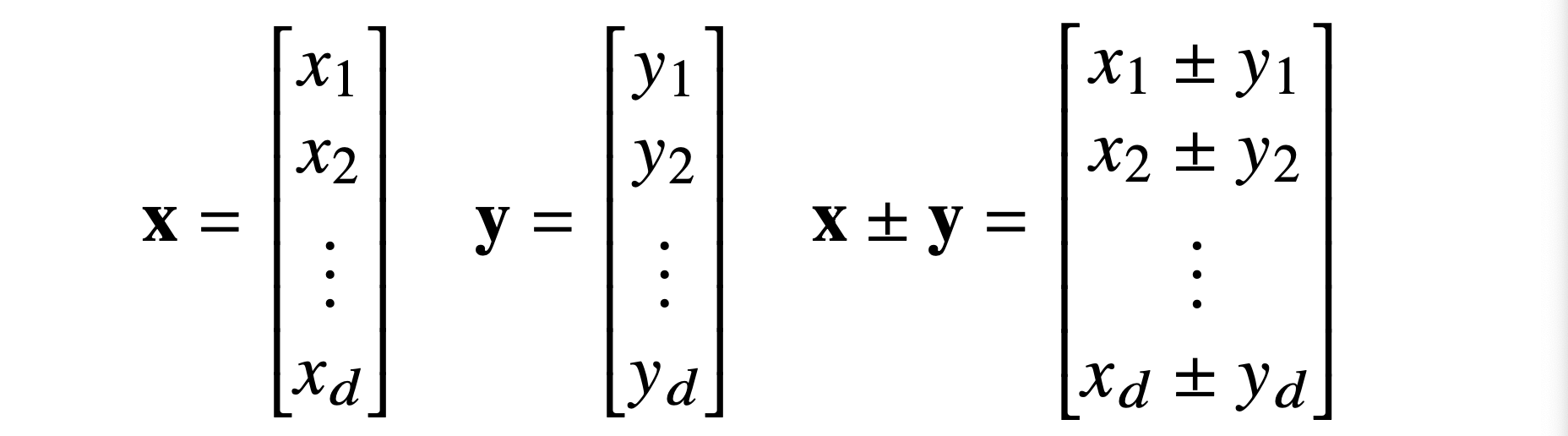
• 성분곱도 계산 가능.
  

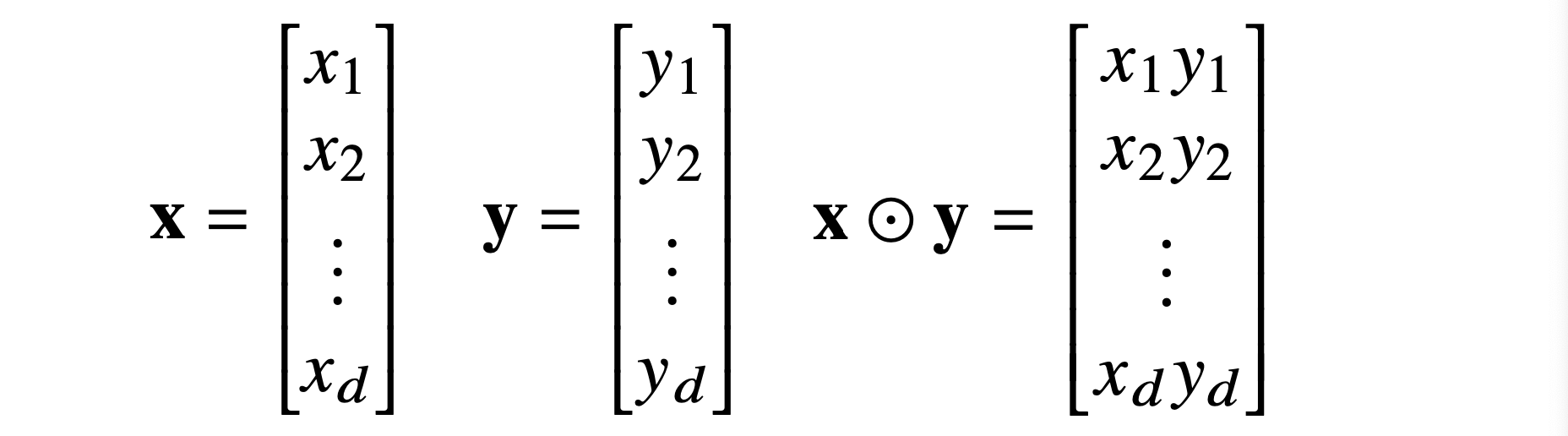
import numpy as np

x = np.array([1, 7, 2])
y = np.array([5, 2, 1])

x + y # array([6, 9, 3])
x - y # array([-4, 5, 1])
x * y # array([5, 14, 2])

2) Addition and Subtraction of Vectors

• 두 Vector의 덧셈과 뺄셈은 다른 Vector로부터 상대적 위치이동을 표현한다.
  

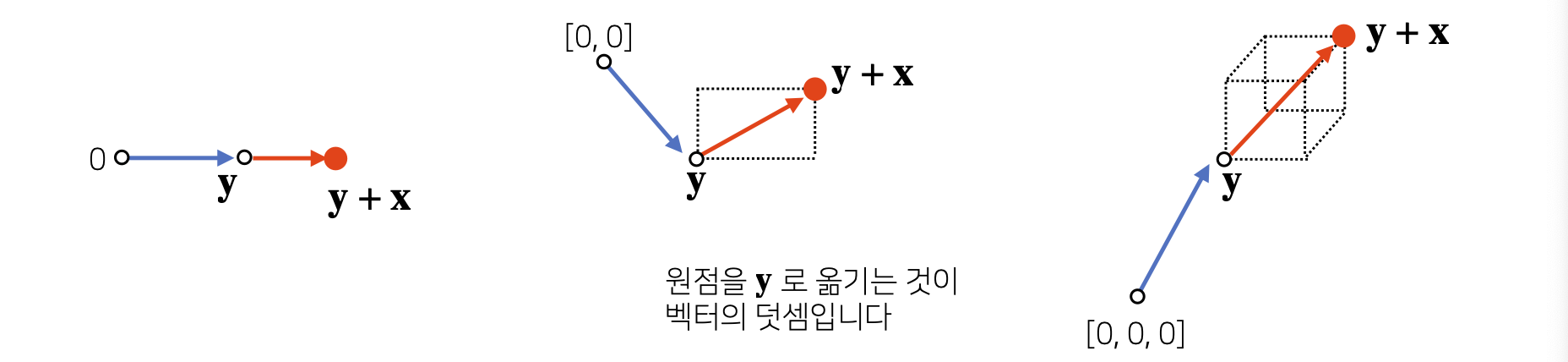
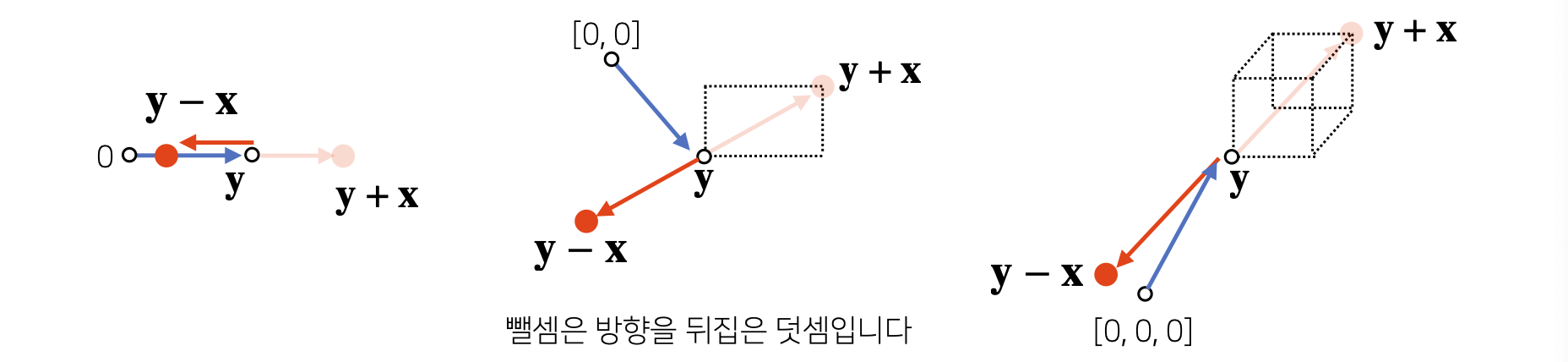
3) Norms of Vectors

• Vector의 Norm : 원점에서부터의 거리
• 임의의 차원 d에 대해 성립한다.
  

def l1_norm(x):
	x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm
    
def l2_norm(x):
	x_norm = x * x
    x_norm = np.sum(x_norm)
    x_norm = np.sqrt(x_norm)
    return x_norm

# L_2-Norm은 np.linalg.norm으로도 구현 가능

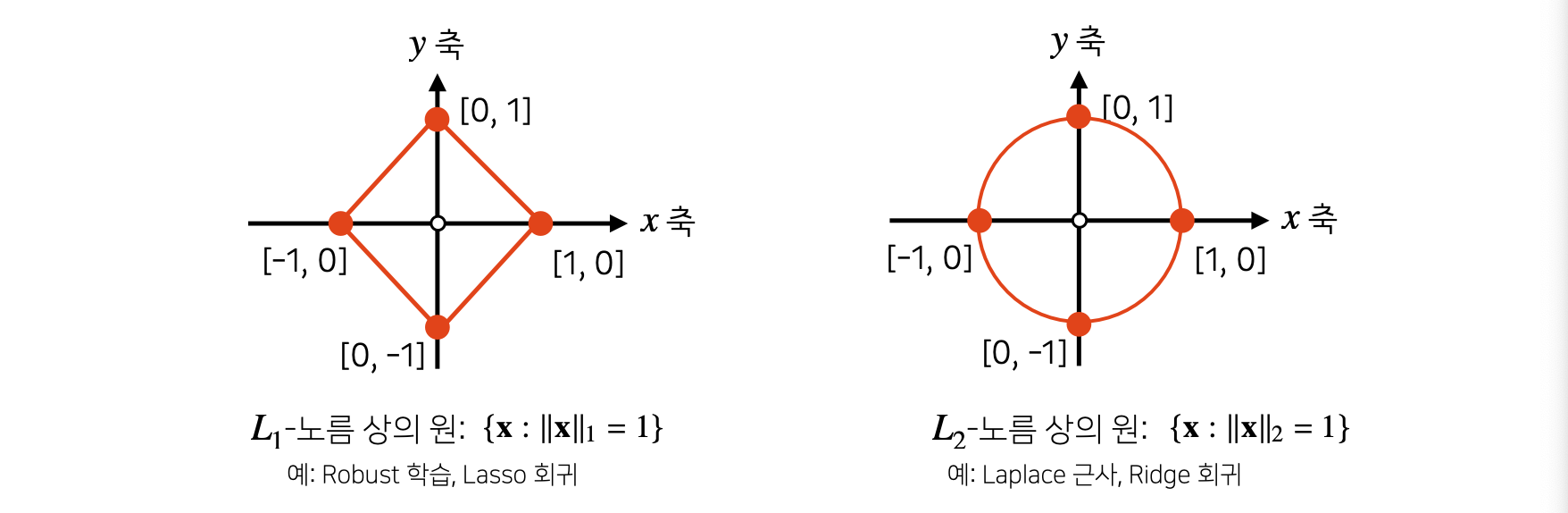
4) Types of Norms

• Norm의 종류에 따라 기하학적 성질이 달라진다.
• L1_Norm에서의 원은 원점으로부터의 거리가 같기 때문에 원이라 할 수 있다.
  

5) Distance Between Two Vectors

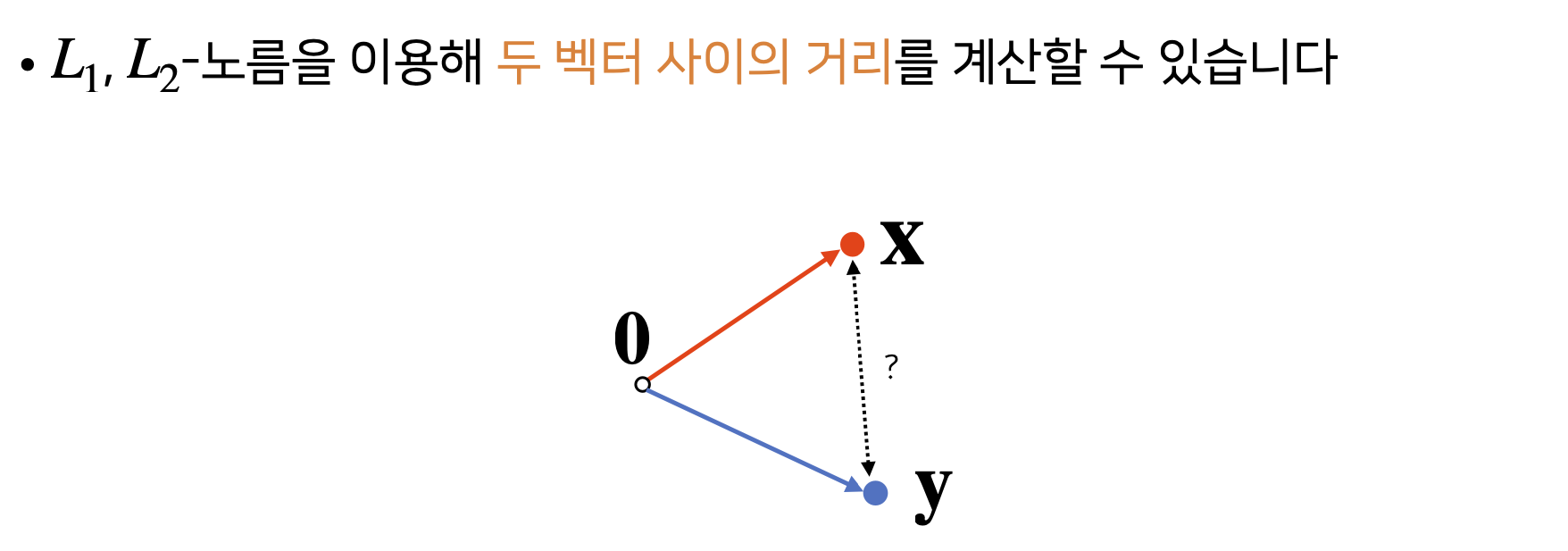
• 두 Vector 사이의 거리를 계산할 때는 Vector의 뺄셈을 이용.
  
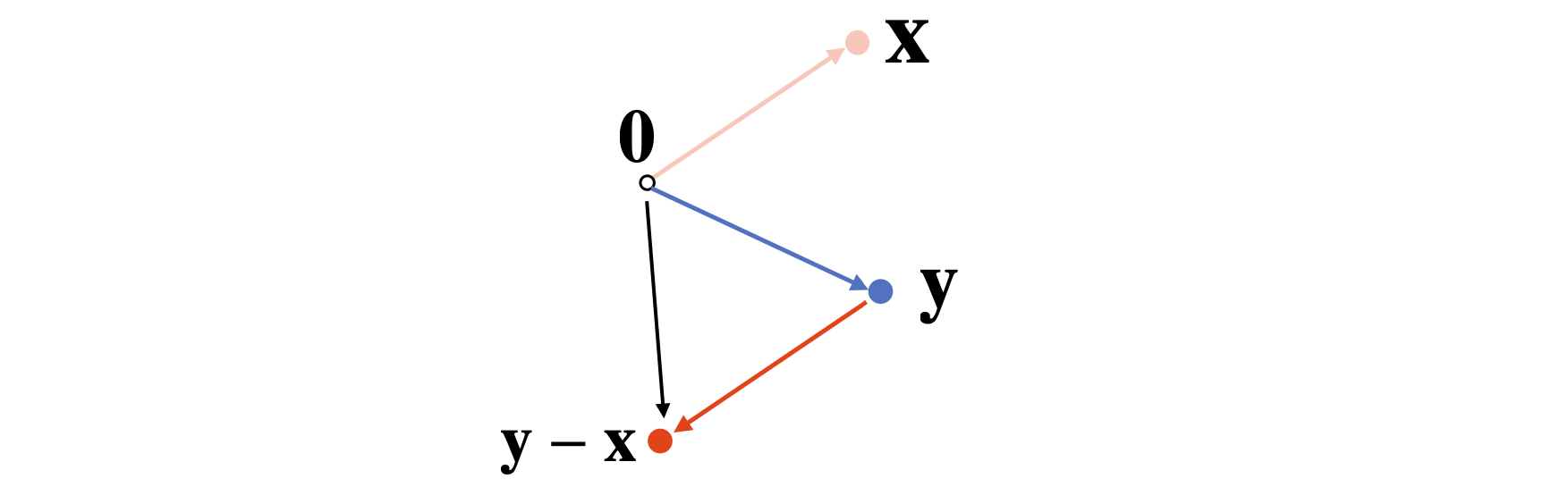
• 뺄셈을 거꾸로 해도 거리는 같다.
  

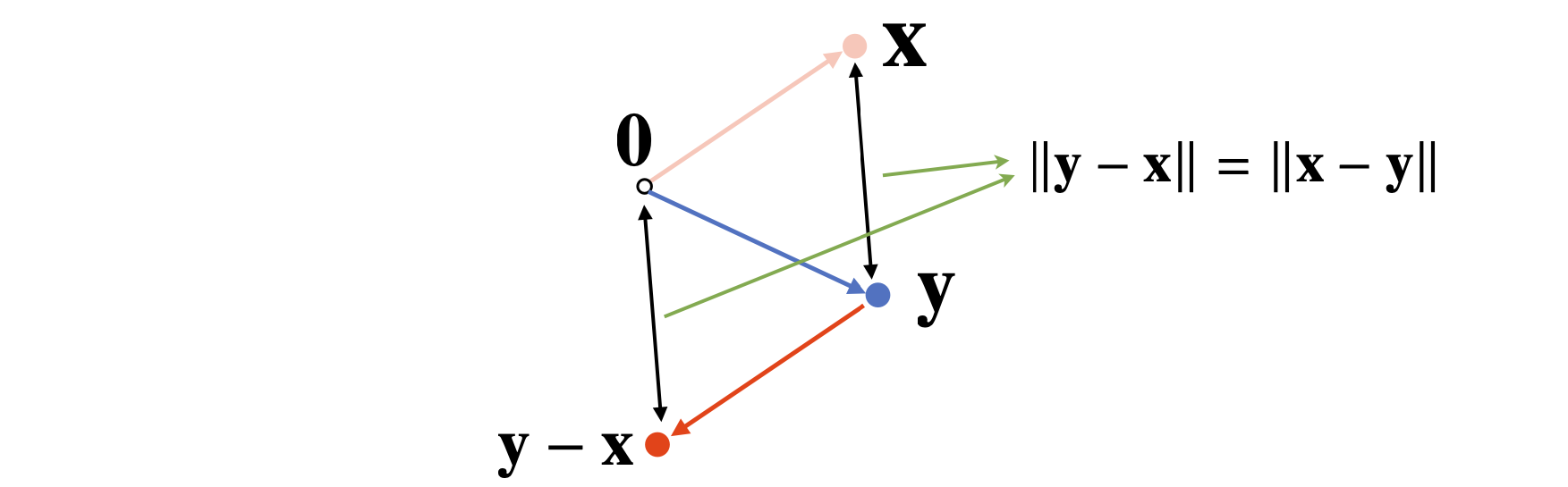
6) Angle Between Two Vectors

• 두 Vector 사이의 거리를 이용.
• 제2 코사인 법칙에 의해 계산 가능.
  

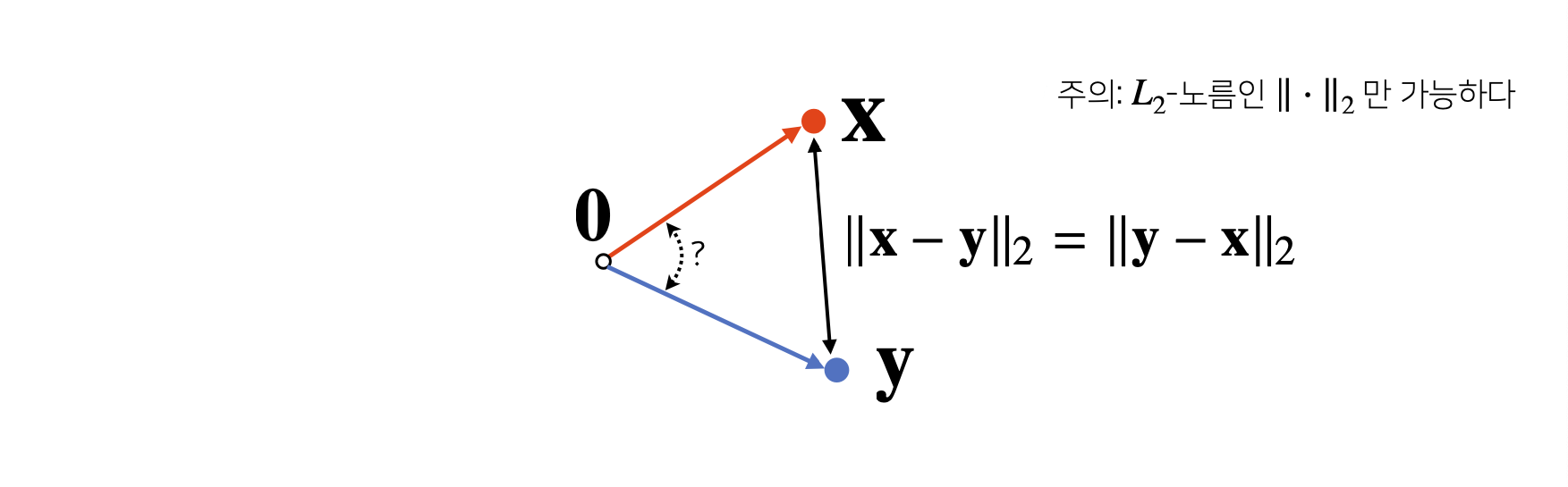
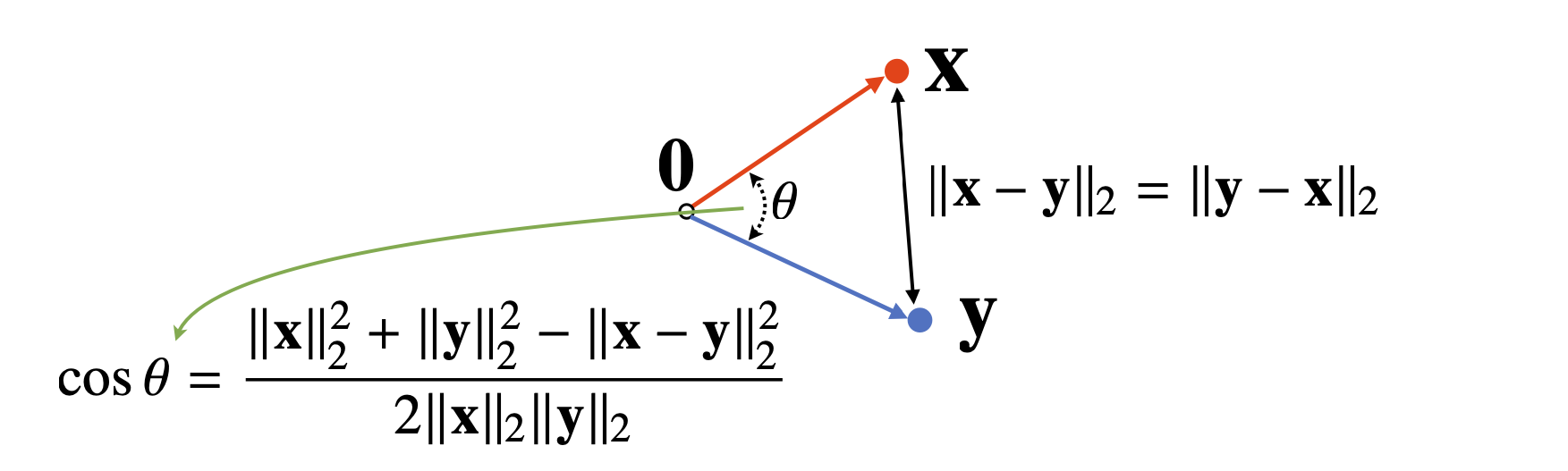
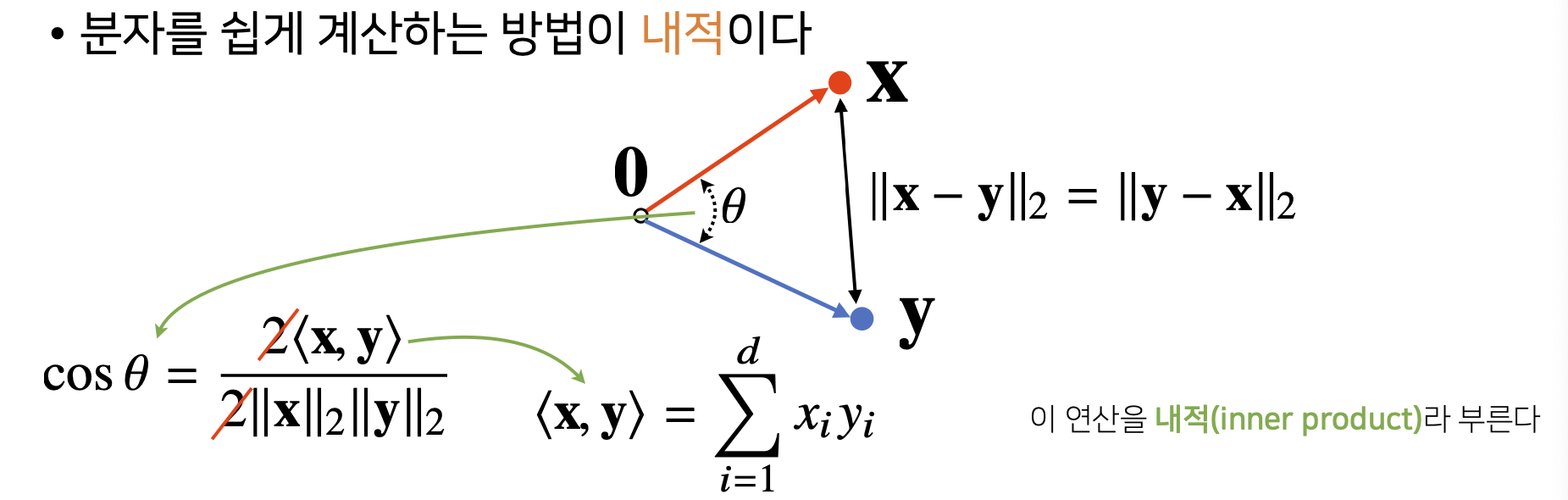
def angle(x, y):
	v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

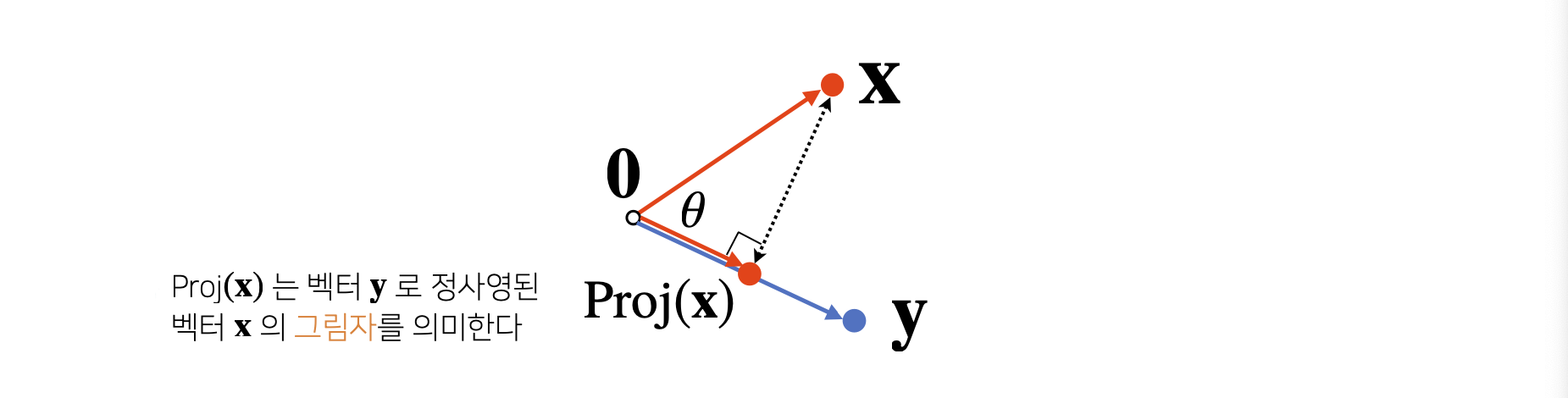
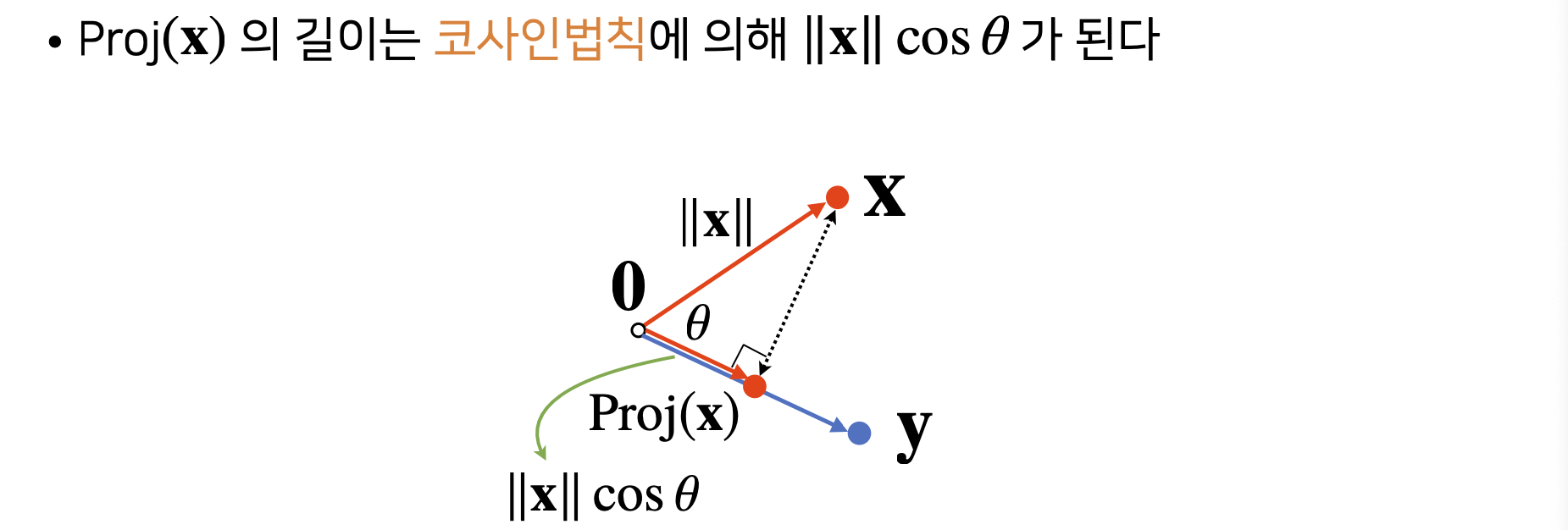
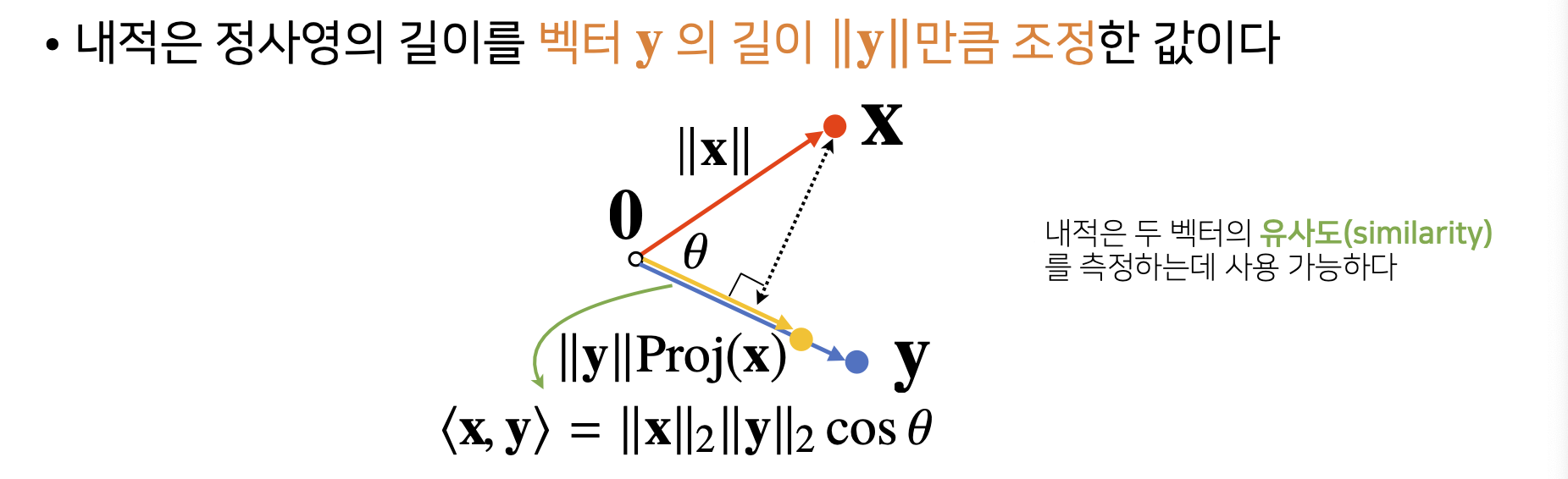
7) Interpreting the Inner Product

• 내적은 정사영(=Orthogonal Projection)된 Vector의 길이와 관련이 있다.