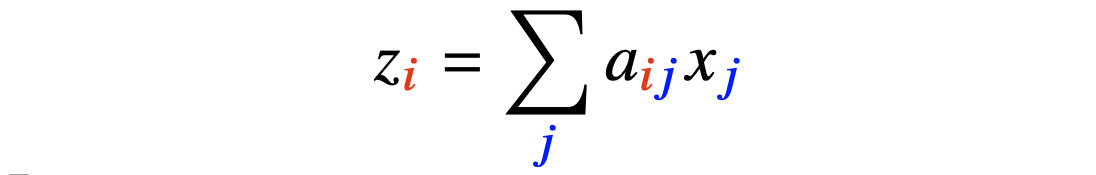Lec9: Mathematics for Artificial Intelligence_Matrix
01_Matrix
1) Matrix?
- Matrix : Vector를 원소로 가지는 2차원 Array
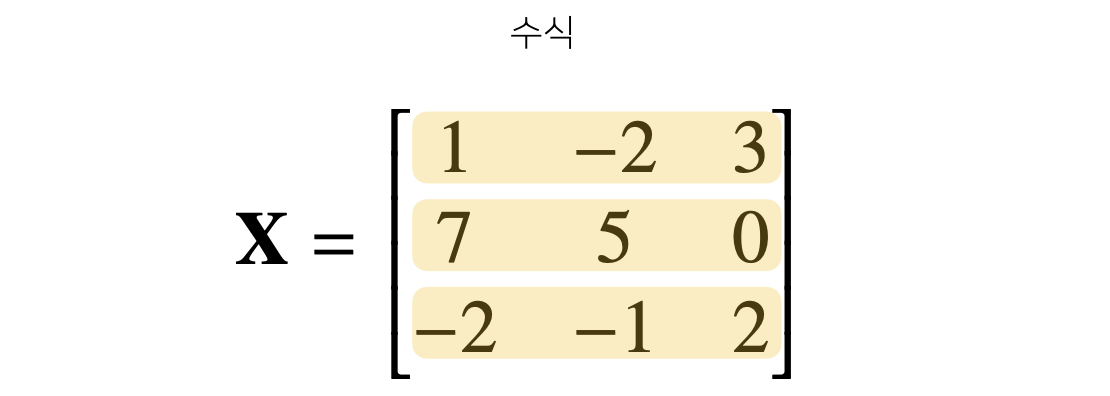
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
- Matrix는 Row와 Column이라는 Index를 가진다.
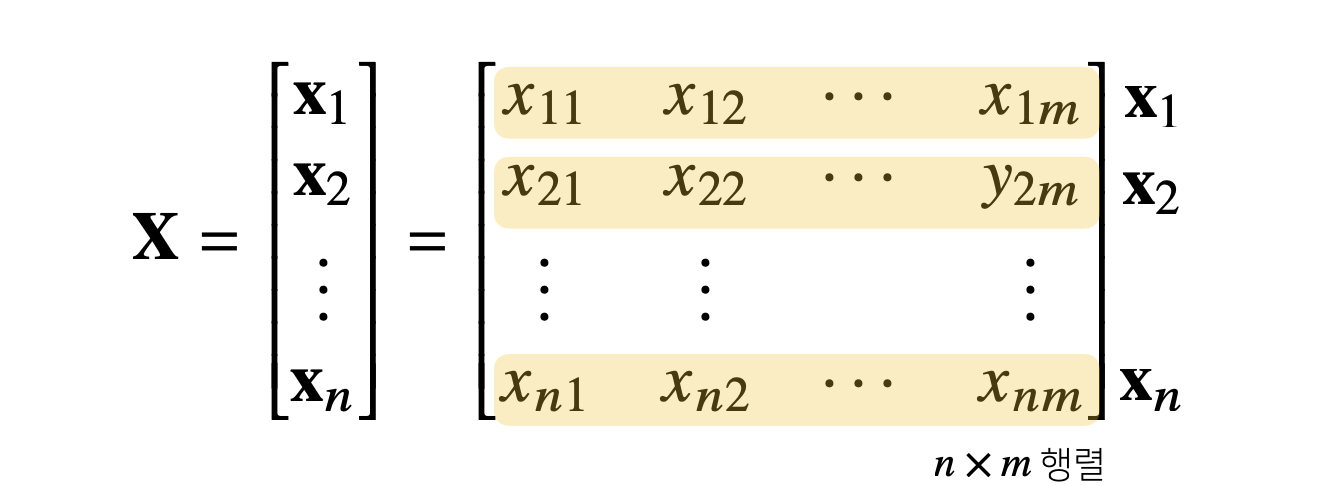
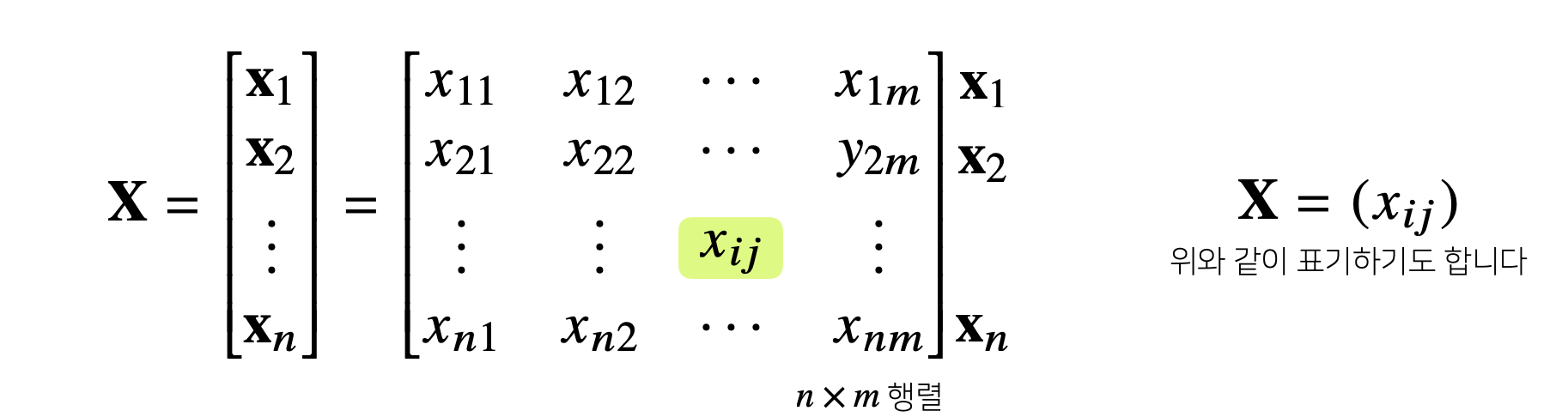
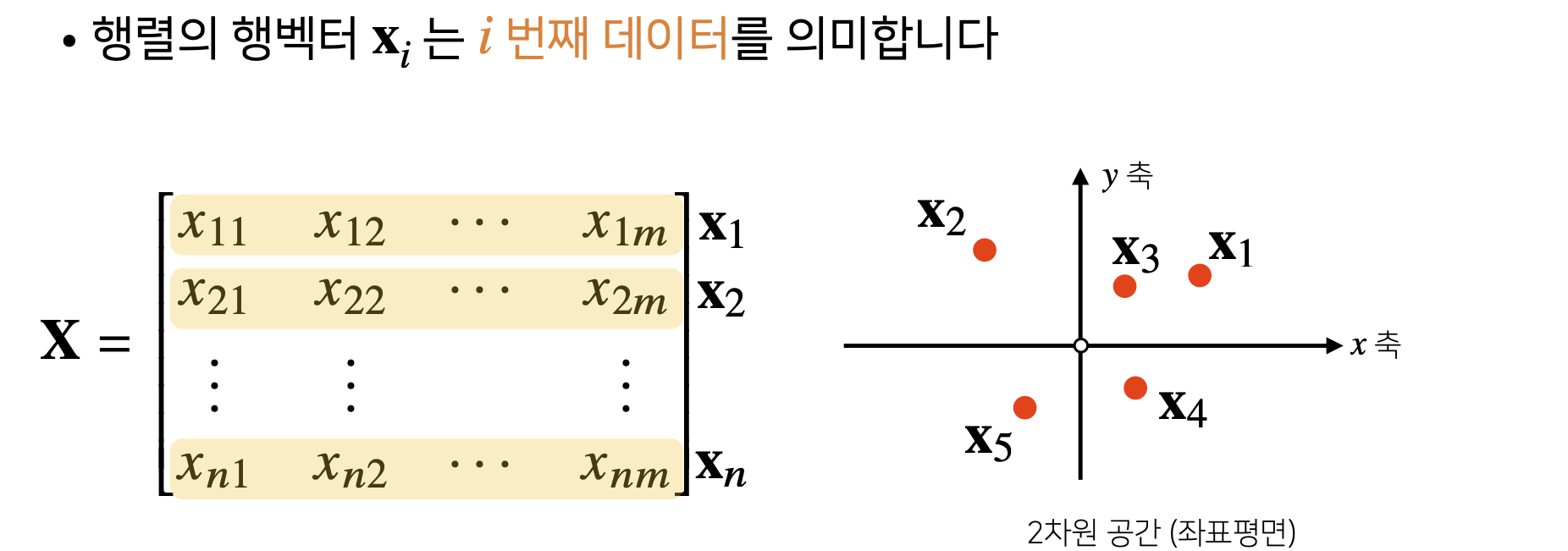
- Matrix의 특정 Row(or Column)을 고정하면 Row(or Column) Vector라고 부른다.

- Transpose Matrix
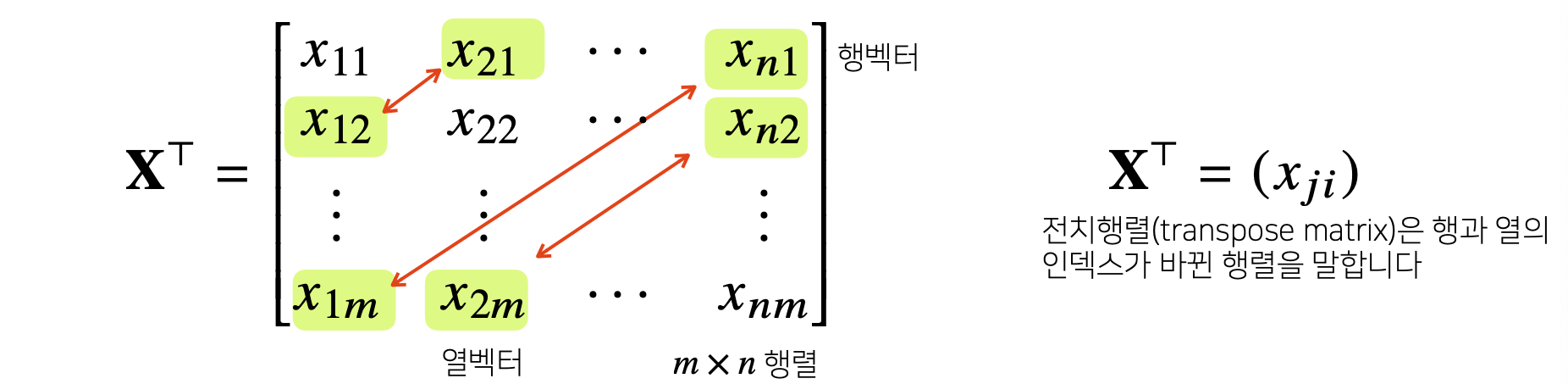
- Vector가 공간에서 한 점을 의미한다면, Matrix는 여러 점들을 나타낸다.
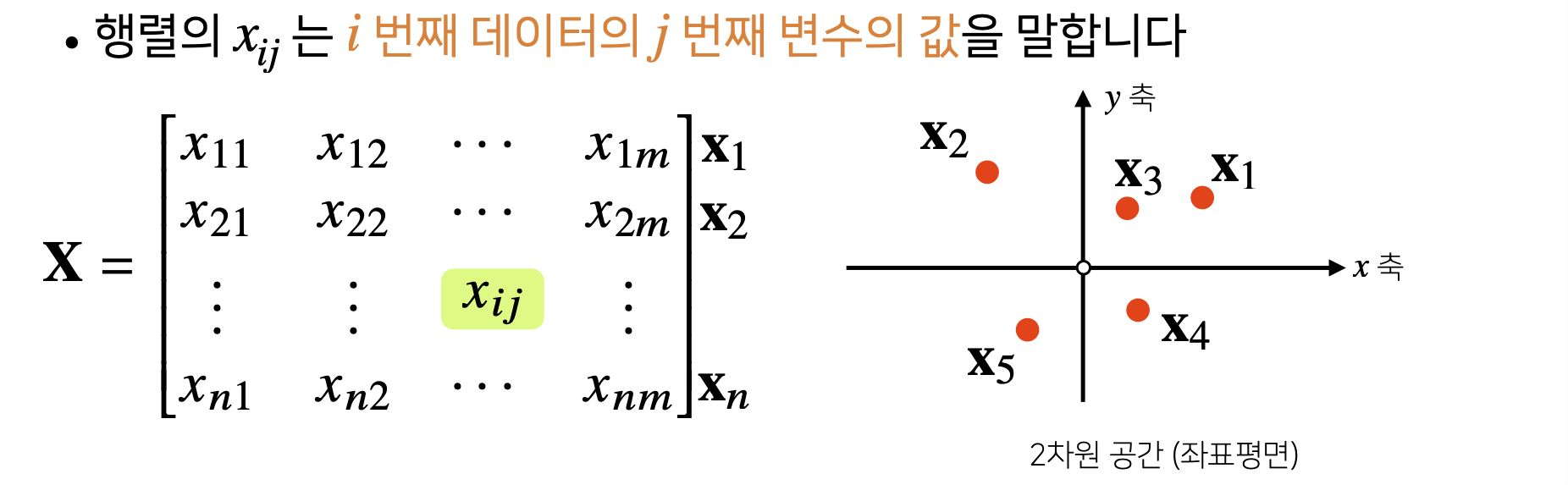
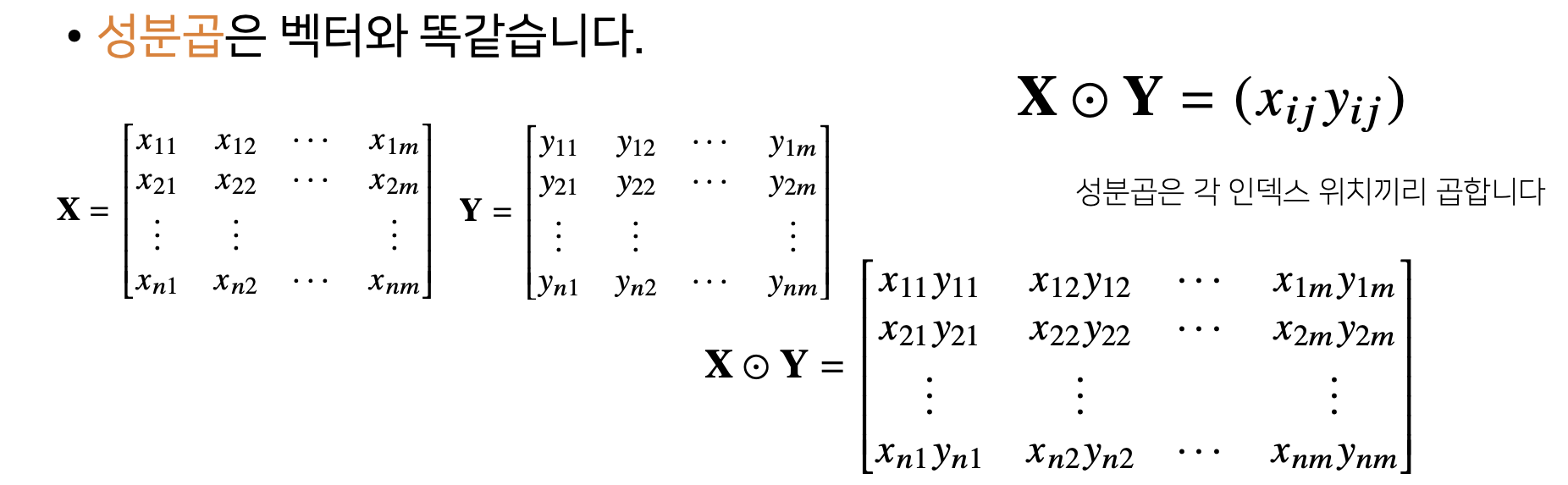
2) Matrix Addition, Subtraction, Component Product, Scalar Product


3) Matrix Multiplication

X = np.array([1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
X @ Y
array([[-8, 6],
[5, 2],
[-5, 1]])
4) Dot Product of Matrix

X = np.array([1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1, -1],
[1, -1, 0]])
np.inner(X, Y)
array([[-5, 3],
[5, 2],
[-3, -1]])
5) Matrix?#2
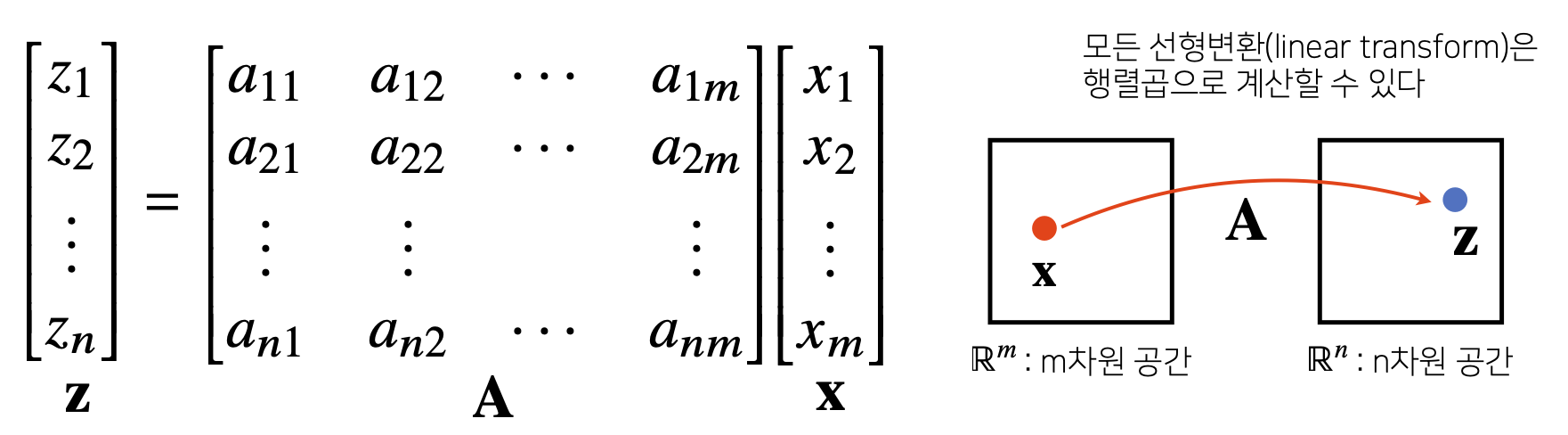
- Matrix는 Vector Space에서 사용되는 연산자(=Operator)로 이해한다.
- Matrix Multiplication을 통해 Vector를 다른 차원의 공간으로 보낼 수 있다.
- Matrix Multiplication을 통해 Pattern을 추출할 수 있고 Data를 압축할 수도 있다.
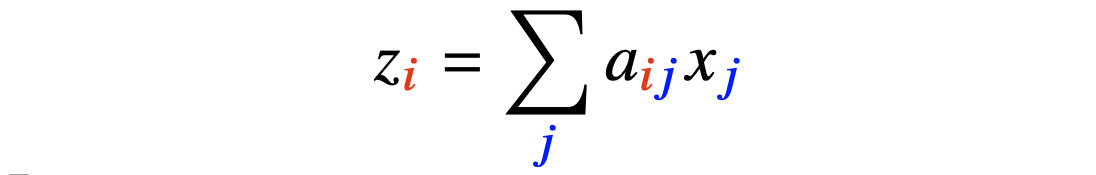
6) Inverse Matrix
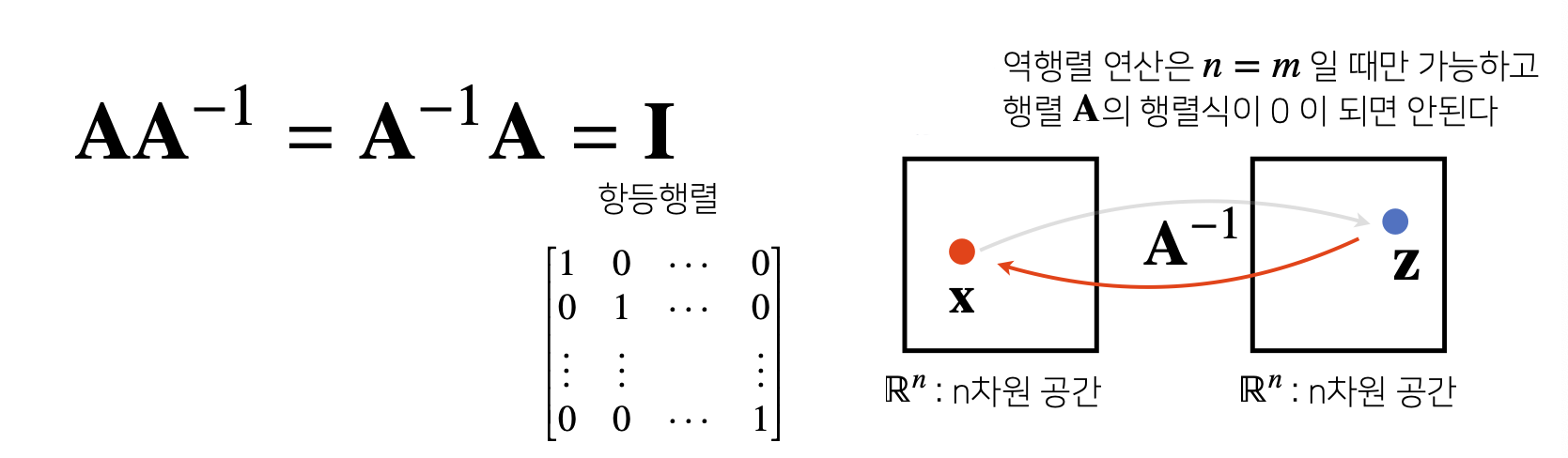
- 어떤 Matrix의 연산을 거꾸로 되돌리는 Matrix : Inverse Matrix
- Row와 Column 숫자가 같고(m=n) 행렬식(=Determinant)이 0이 아닌 경우에만 계산 가능
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
np.linalg.inv(X)
X @ np.linalg.inv(X)


- 만약 Inverse Matrix를 계산할 수 없다면 Pseudo-Inverse 또는 Moore-Penrose Inverse Matrix를 이용.

Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
np.linalg.pinv(Y)
np.linalg.pinv(Y) @ Y


7) Apply#1 : Solve System of Equations
- np.linalg.pinv를 이용하여 연립방정식의 해를 구하자.
- 연립방정식은 Matrix를 사용하면 Ax = b와 같이 표현 가능.


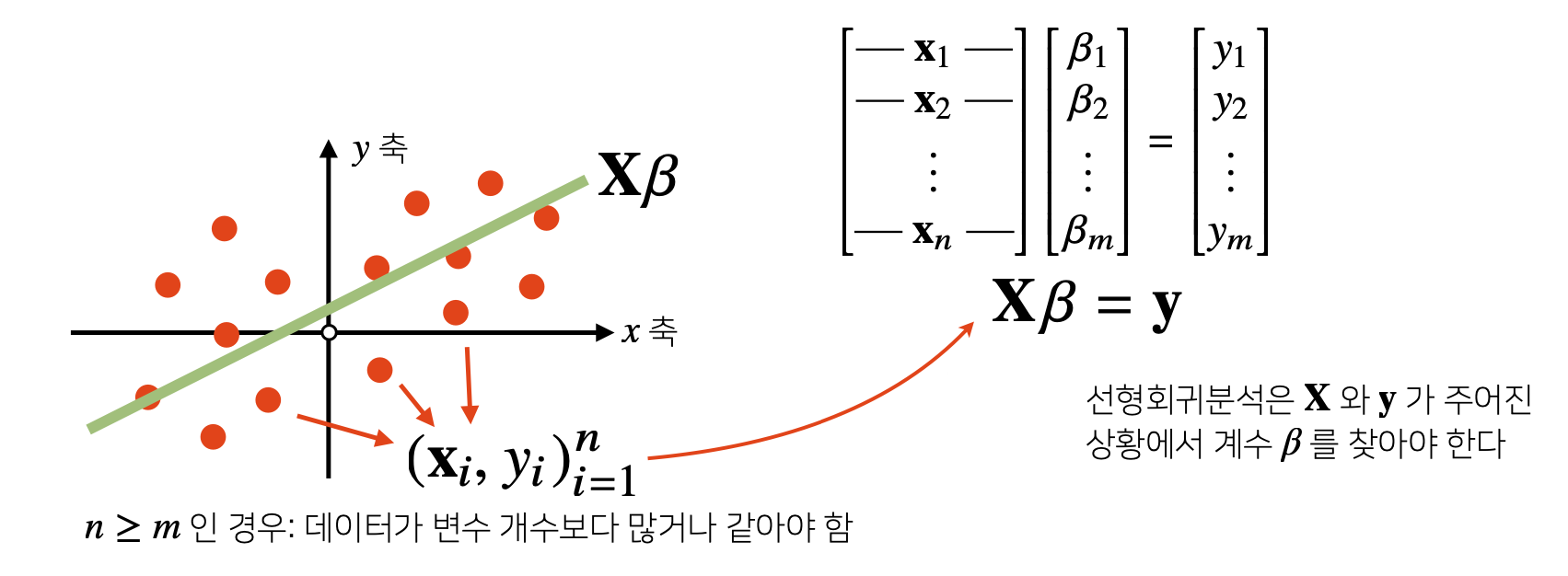
8) Apply#2 : Linear Regression Analysis
- np.linalg.pinv를 이용하면 Data를 Linear Model로 해석하는 선형회귀식을 찾을 수 있다.
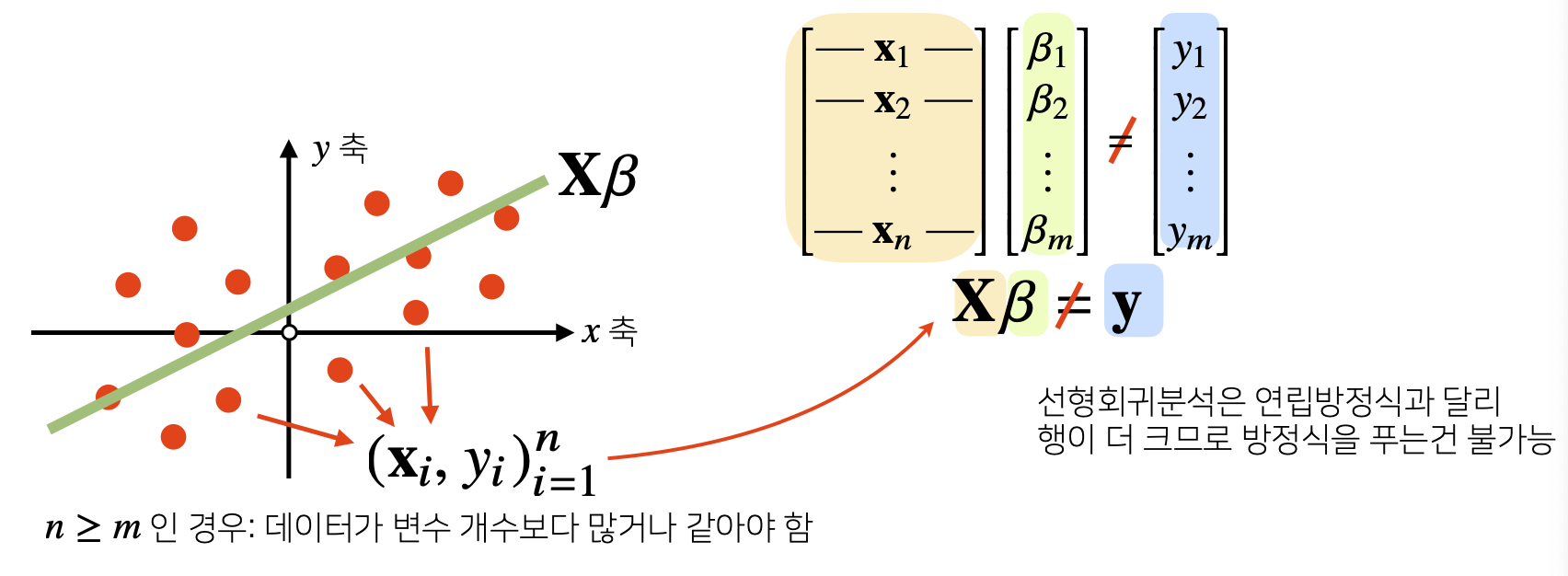
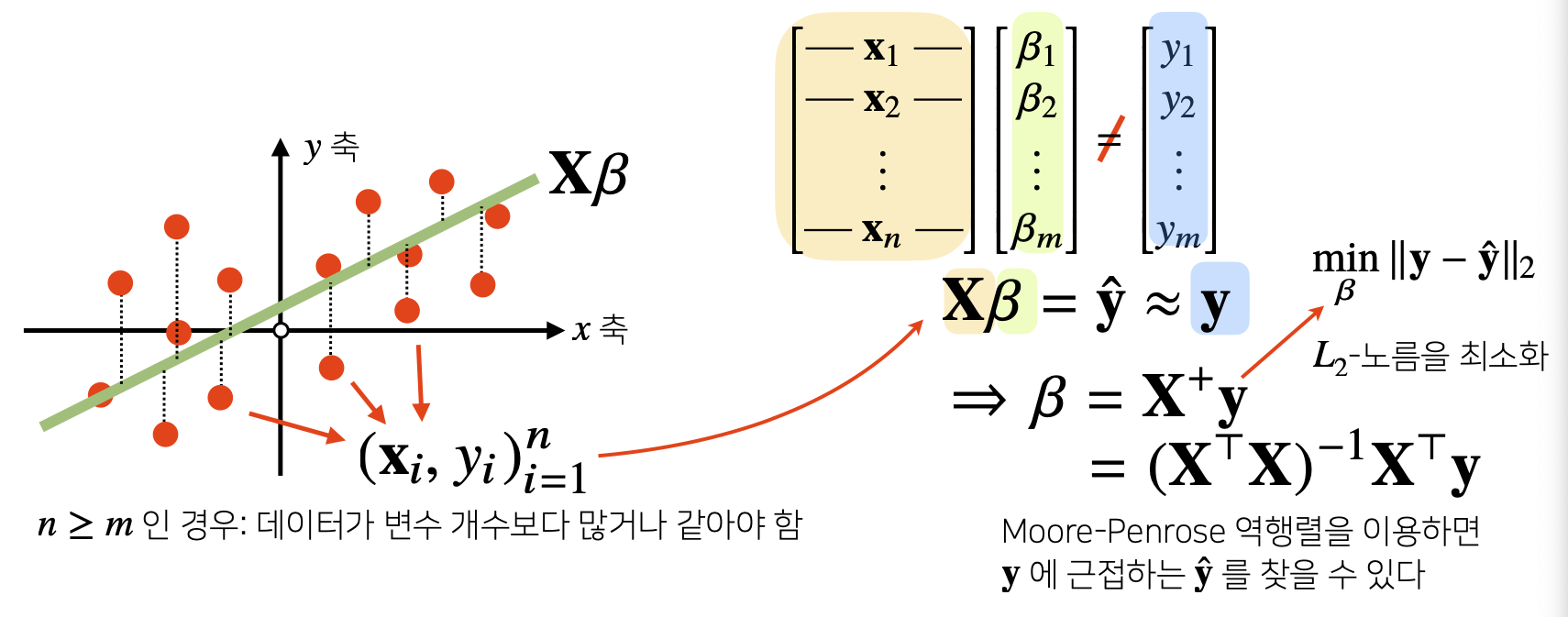
- sklearn의 LinearRegression과 같은 결과를 가져올 수 있다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
y_test = model.predict(x_test)
X_ = np.array([np.append(x, [1]) for x in X])
beta = np.linalg.pinv(X_) @ y
y_test = np.append(x, [1]) @ beta