[Aiffel] 아이펠 35일차 개념 정리 및 회고

1. 머신러닝 개념 정리

참고

머신러닝의 목표
모델이 표현하는 확률 분포와 데이터의 실제 분포를 최대한 유사하게 만드는 최적의 파라미터 값을 찾는 것

1) 모델 파라미터

$y=f(x)=ax+b\ \ \ \ \ \ a,b∈R$라고 할 때 (a,b)가 위치하는 $R$ 공간을 parameter space라고 함

2) prior likelihood posterior

1. 베이시안 머신러닝
   모델 파라미터를 고정된 값이 아닌 확률 변수로 보기 때문에, 불확실성을 가지고 있다고 전제한다.

2. 용어 설명

   전제
   어떤 데이터 집합 $X$가 주어졌을 때 데이터가 따르는 확률 $p(X)$가 있을 것. 이때 $p(X)$를 가장 잘 나타내는 일차함수 모델 $y=ax+b=θ^{⊤}x$를 찾는 것이 목표임.

   $p(θ)$	prior probability, 사전확률, 데이터를 관찰하기 전에 parameter space에 주어진 확률 분포 일반적인 정규분포, 데이터 특성이 반영된 특정한 확률 분포 모두 가능
   $p(X=x∣θ)$ or $L(θ∣x)$	likelihood, 가능도, 우도, prior 분포를 고정시켰을 경우 주어진 파라미터 분포에 대해 가지고 있는 데이터가 얼마나 그럴듯한지 계산한 값을 나타내는 것 높을 수록 데이터의 분포를 모델이 잘 표현하는 것 최대 가능도 추정(maximum likelihood estimation, MLE): likelihood의 값을 최대화하는 방향으로 모델을 학습시키는 방법
   $p(θ∣X)$	posterior probability, 사후확률, 데이터를 관찰한 후 계산 되는 확률 사후 확률 추정(maximum a posteriori estimation, MAP): posterior를 최대화하는 방향으로 모델을 학습시킴

3. posterior와 prior, likelihood의 관계

• 데이터가 따르는 확률분포 $p(X)$를 알 수 없기 때문에 posterior $p(θ∣X)$의 값 또한 직접 구할 수 없다.
• 우변의 식에서도 $p(X)$로 나누는 부분이 있기 때문에 우변의 식으로도 $p(θ∣X)$는 계산 불가능.
• 다만 데이터가 바뀌지 않으니 p(X)는 고정된 값이고 likelihood와 prior는 계산이 가능하기 때문에 우변을 최대화하는 파라미터 값을 찾을 수 있는 것.

---

2. CS231n Lecture 7

참고

• [cs231n 7강]
• [CS231n] Lecture 7. Training Neural Networks II

1) Optimization: Problems with SGD

1. SGD & BGD

	SGD	BGD
방식	데이터 중 무작위로 하나를 선택해 기울기를 계산함. 이를 경사 하강 알고리즘에 적용	학습 데이터셋 전체를 하나의 배치로 취급해 학습시킴
batch size	1	데이터 전체
장점	Vanila gradient descent에 비해 학습 속도가 빠름	병렬처리에 유리
단점	노이즈가 심함	메모리가 많이 필요

2. SGD 문제점

• 학습 속도의 저하
  • 예시)
    
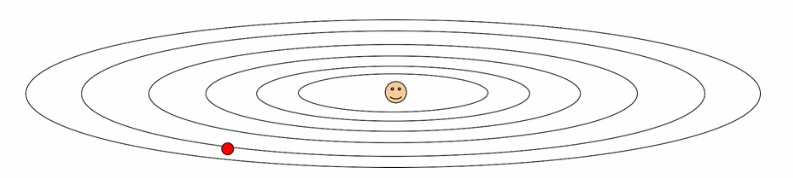
    • 빨간색 점 위치에서 웃는 모양을 찾아간다고 하면, x축 방향으로는 완만하게, y축 방향으로는 빠르게 움직일 것
      
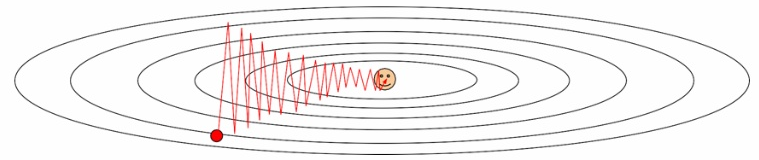
    • 위와 같은 움직임을 보이기 때문에 학습 속도가 저하됨.
• local minima에 빠지기 쉬움
• saddle point(순간 기울기가 0에 가까워지는 지점)에서도 멈출 수 있음: 고차원에서 더 일반적으로 일어나는 문제
• 노이즈 문제

2) SGD 외의 방법

종류	계산식	설명
Momentum		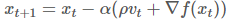SGD가 기울기가 0인 지점에서 문제를 일으키는 경우를 방지하기 위해 Momentum 등장 물리학적 관점에서 가속도를 부여한다고 생각하기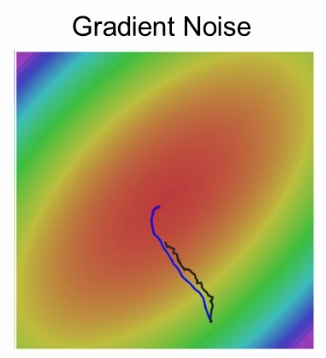momentum이 없을 때(회색) vs momentum이 있을 때(파란색)
Nesterov Momentum		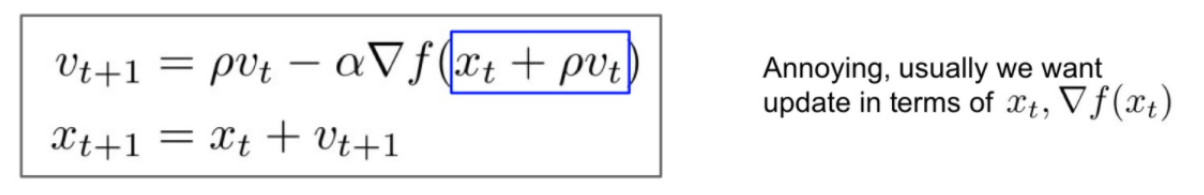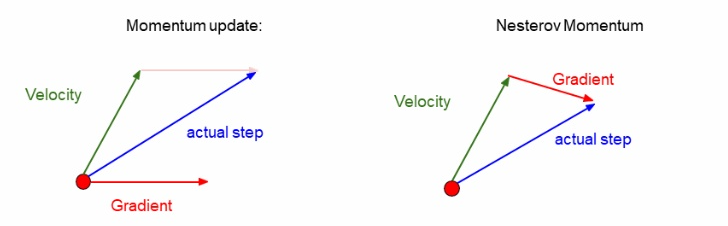직전 지점의 velocity 벡터의 종착점을 예상해, 그 지점에서의 gradient 합하여 actual step를 구하는 방법 convex optimization에서 뛰어난 성능을 보여주지만, 고차원 딥러닝에선 non-convex graph가 더 많다..
AdaGrad		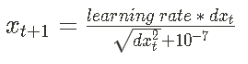각각의 매개변수에 적합하게 갱신해줌. 수직, 수평축의 업데이트 속도를 적절하게 맞춰줌 문제: cache값이 누적됨에 따라 학습이 진행되다보면 가중치가 0이 되어 학습이 종료될 수 있음
RMSProp		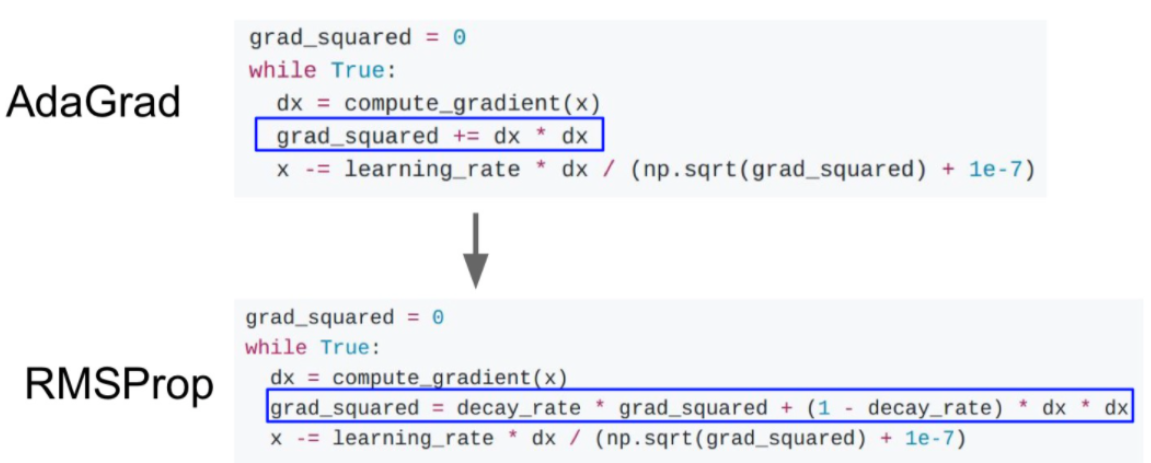AdaGrad의 학습 종료 문제를 개선한 알고리즘 누적된 grad_squared항에 decay_rate를 곱하고, 현재의 dx항에는 (1-decay_rate)를 곱해 grad_squared가 누적되는 속도를 줄임
Adam		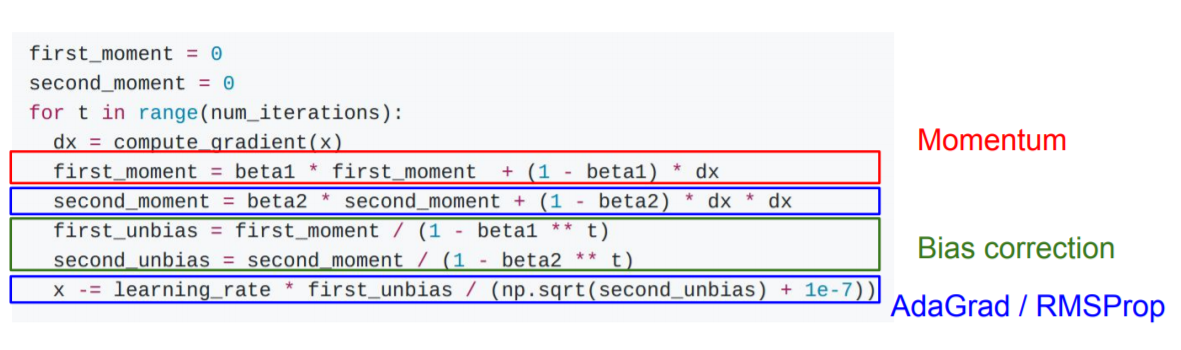RMSProp + Momentum

3) Learning Rate Decay

• 문제: 위에 나온 빨간색 그래프와는 달리 오른쪽과 같이 어느 순간 loss 감소가 더딘 구간이 여러 군데 존재하기 때문에, 이럴 때마다 learning rate를 줄여야 함. 이러한 생각에서 착안한 방식이 learning rate decay
• 하나의 방법: 초기에 큰 학습률을 사용해 빠르게 최소 loss에 수렴하도록 한 후, 뒤로 갈 수록 학습률을 낮추어 더 세밀하게 학습하도록 함
• 많이 사용하는 방법: exponential decay

4) First-Order Optimization & Second-Order Optimization

1차 근사	2차 근사
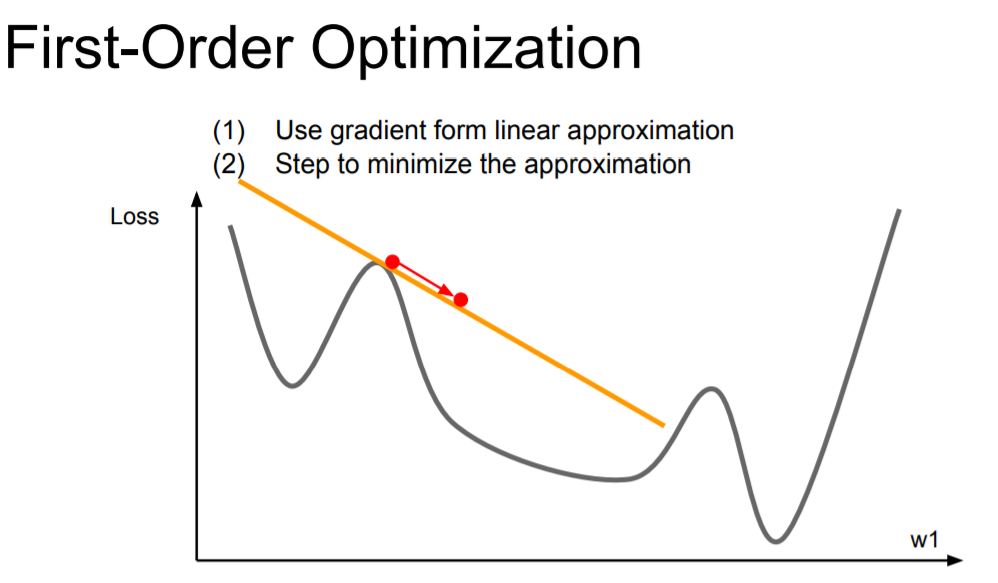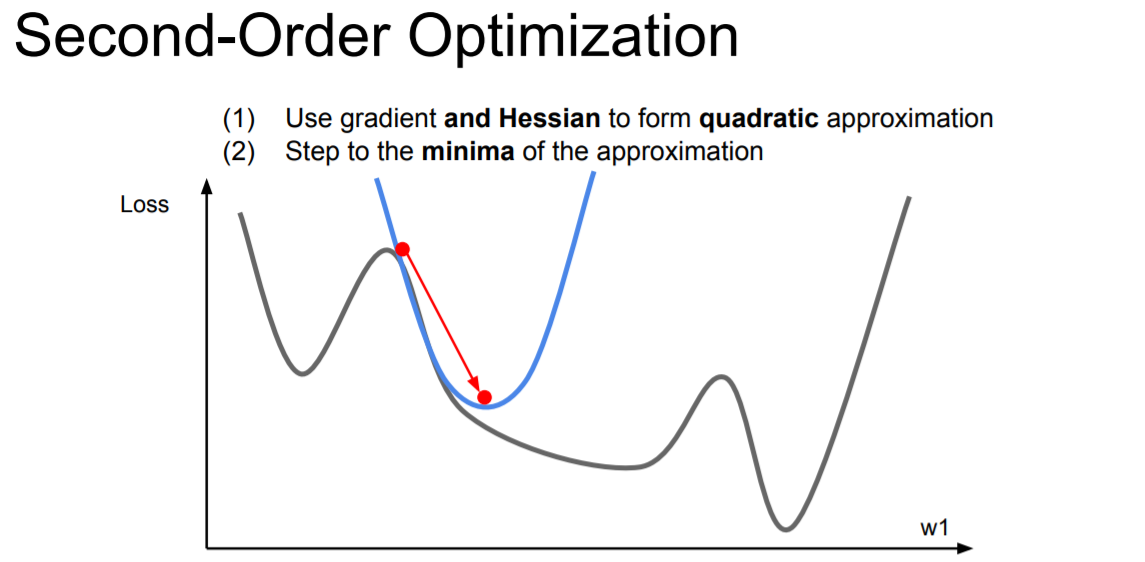linear approximation, 위에 언급된 모든 방법이 해당	특정 지점에서 해당 기울기를 갖는 2차 함수를 구하는 것 1 지점에서 2차 근사함수를 구한다. 이 2차 근사함수의 최소점을 갖는 2번 지점이 다음 가중치로 갱신됨. 이런 식으로 계산을 반복하면 1차 근사보다 빠르게 loss가 0인 지점을 찾아갈 수 있다.

• 2차 근사를 deep learning에 사용할 경우 차원이 매우 크기 때문에 시간복잡도가 높아져 잘 사용하지 않음

• L-BFGS

  • Hessian을 근사시켜서 사용하는 방법
  • full batch에서 성능이 좋지만 mini batch에선 그닥

5) Model Ensembles + Regularization

training set에 대한 최적화를 다 거친 상황에서 validation data를 이용해서도 알고리즘이 잘 작동하게 하려면 어떻게 해야할까?

1. Ensembles
   • 여러 개의 독립된 모델을 학습시켜 각각의 결과의 평균값을 이용하는 것
   • 90% 이상인 상태에서 1~2%의 성능을 올리기 위해 사용
2. Snapshot ✔✔✔🤔
   • 독립적으로 여러 개의 모델을 학습시키는 방법과는 다름
   • 하나의 모델을 사용하는데 여러 개의 snapshot을 이용함
   • test를 할 때 여러 snapshots(구간을 정해놓은 지점)에서 나온 예측값의 평균을 이용
     
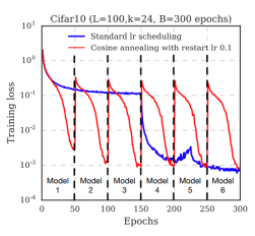
     learning rate를 크게 함 ⇒ loss exploded ⇒ 다른 minima에 가던 것 기억 ⇒ 다양한 minima point를 갖는 모델의 snap shot을 얻을 수 있음 ⇒ 이를 이용해 앙상블
3. Regularization

Regularization
과적합을 줄이기 위해 규제항을 추가하는 방법으로, 앙상블을 사용하지 않고 모델의 성능을 향상시킬 수 있다. L1과 L2는 NN에선 잘 활용하지 않는다.

Dropout	- forward pass 과정에서 일부 뉴런만을 활용한다. - 일부 뉴런의 activation 값을 0으로 만들어 다음 레이어에 반영하기 때문에 결과적으로 영향을 끼치지 않는다. - feature 간의 상호작용을 방지함 = overfitting을 어느 정도 방지 - train time: forward pass 마다 dropout을 무작위로 하기 때문에 그 때마다 다른 모델을 학습하는 것과 같은 효과가 나타난다. 단일 모델로 앙상블과 같은 효과를 낼 수 있는 것. - test time: 결과를 도출할 때마다 바뀌면 안되기 때문에 dropout의 무작위성을 average out 하려고 함. 이때 적분을 통한 누적확률값을 이용하긴 어렵기 때문에 local cheap방식으로 도출된 근사값을 사용함
Data Augmentation	- 학습용 데이터의 이미지를 무작위로 변환 시킨다. 이때 레이블은 그대로 유지됨. - 이미지의 일부를 크롭하거나 반전, 밝기를 바꾸기도 함 - train time에는 stochasticity(확률)가 추가되고 test time에는 marginalize out이 가능
Dropconnect	activation의 값이 아닌 weight를 랜덤으로 0으로 조정하는 방법
Fractional Max Pooling	자주 쓰이진 않음. pooling 연산 시 spot을 랜덤하게 연산하는 방법 test 시 random성을 없애기 위해 pooling region을 고정 or 여러 개의 region을 average out 시킴
Stochastic Depth	train time에서 일부 레이어를 제외하고 학습, test time에는 네트워크를 모두 사용
Transfer Learning	전이학습, 데이터 값이 원하는 양보다 모자를 때 사용

6) transfer learning

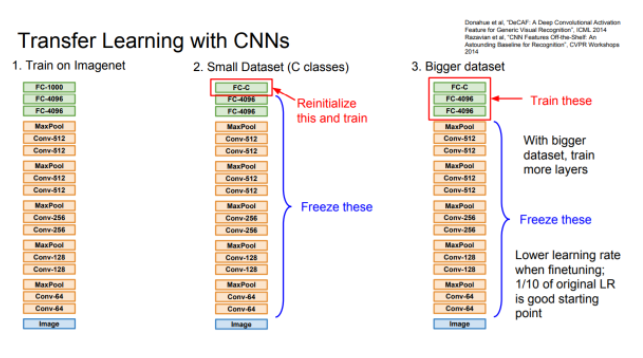
• 많은 양의 데이터로 이미 학습시킨 이력이 있는 알고리즘을 가지고 온다. 이때 C개의 적은 클래스를 분류하는 알고리즘을 만들고자 하며, 현재 주어진 데이터의 수도 적은 경우 가장 마지막 FC layer, 즉 최종 class score을 이용해 사진을 분류하는 레이어의 가중치를 초기화시킨다.

• 여기서 원하는 만큼 차원을 줄이고, 마지막 레이어만으로 주어진 데이터를 학습시킴
  

  

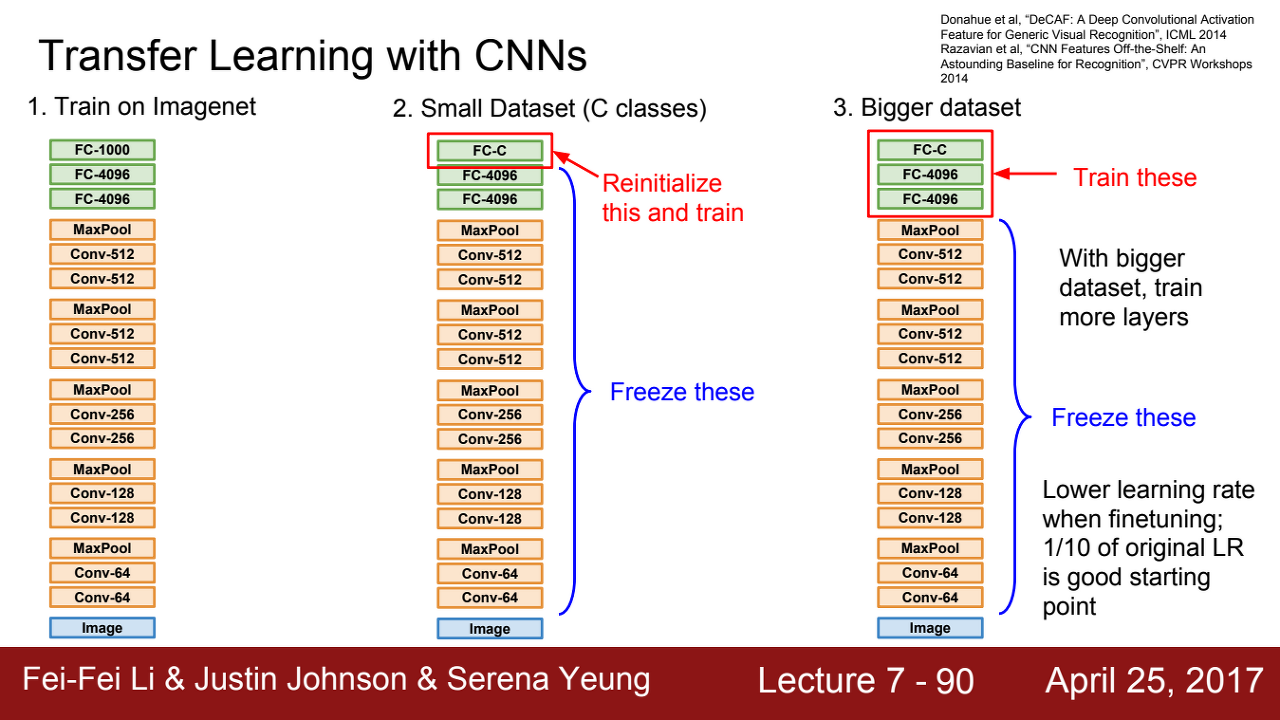
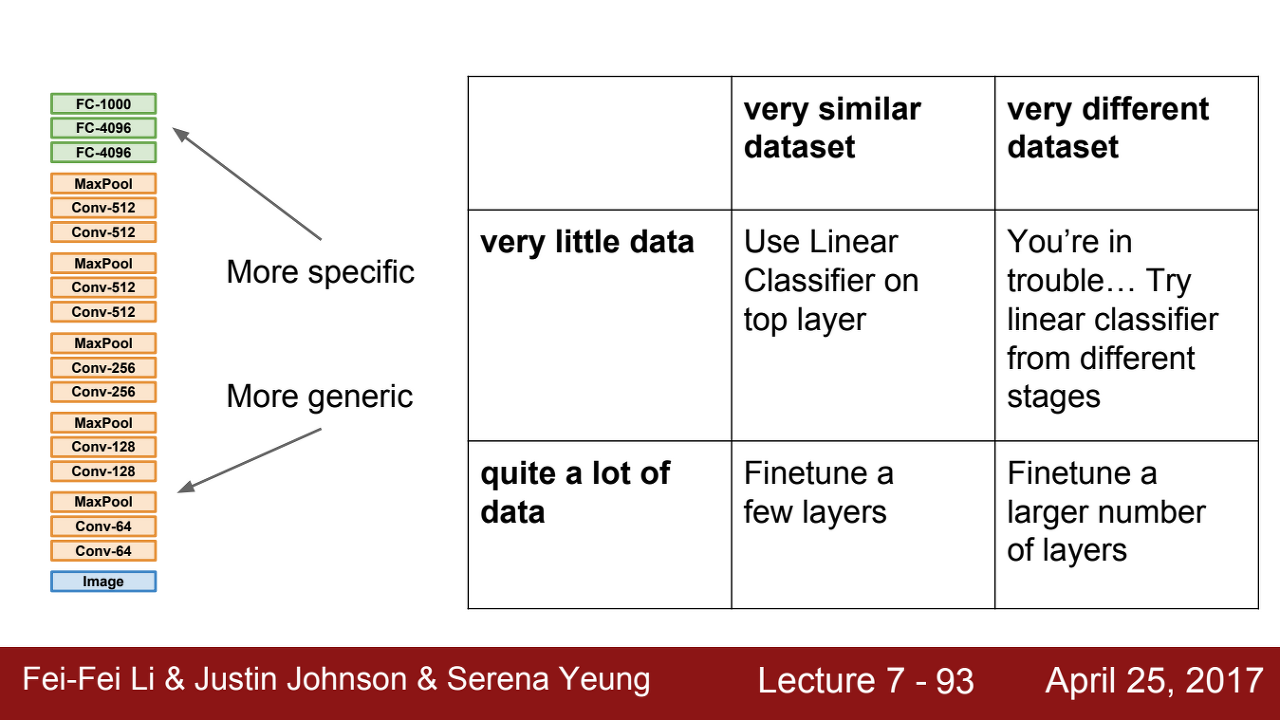
  • 데이터의 많고 적음, 유사도를 바탕으로 위와 같은 네 가지 선택을 할 수 있음
  • fine tuning: 이미 학습된 모델을 기반으로 아키텍쳐를 새로운 목적에 맞게 변형, 이미 학습된 모델 weight로부터 학습을 업데이트 하는 방법

3. 회고

이전에 한 번씩 들어본 내용을 정리하는 거였지만 들어봤던 것만 기억나지 정확히 어떤 내용인지 기억이 안나서 역시 복습이 중요한 걸 다시 한 번 느꼈다. 위에 공부했던 부분 중에선 snapshot이 잘 이해가 안돼서 다시 봐야할 거 같다. 그리고 sgd에서도 학습에 걸리는 시간에 관련해서 생각할 수록 헷갈려서 같이 다시 봐야할 거 같다. 그리고 fundamental node 진행하면서 역시 수학이 부족함을 느꼈다. 거의 이해 못한 거 같다..