
< 심층신경망의 학습 과정 >
- Deep learning을 학습하기 위한 구체적인 기법들
- Gradient descent
- Back propagation
- Gradient vanishing & batch normalization
1. 어떻게 학습하는가?
-> 최적화하고자 하는 파라미터 W(learnable parameter, 가중치)를 gradient descent하여 학습시킨다.
Loss function이 최소화가 되도록!
loss function에 대해서 각각의 파라미터들에 대한 미분 값을 구하고, 그 미분값을 사용해 현재 주어진 파라미터 값을 가지고 미분 방향의 -방향으로 learning rate를 곱해서 파라미터를 업데이트한다.
그러나 original gradient descent의 방식으로는 왔다갔다하면서 수렴하기 때문에 불필요한 반복 횟수가 생길 수 밖에 없다.
그래서 여기에서 변형하는 다양한 알고리즘들 (GD, momentum, adagrad, RMSProp, Adam 등등 앞에서 살펴본 GD 변형방법)을 사용한다.
ADAM이 gradient descent중 가장 좋은 방법!
2. Forward propagation & back propagation
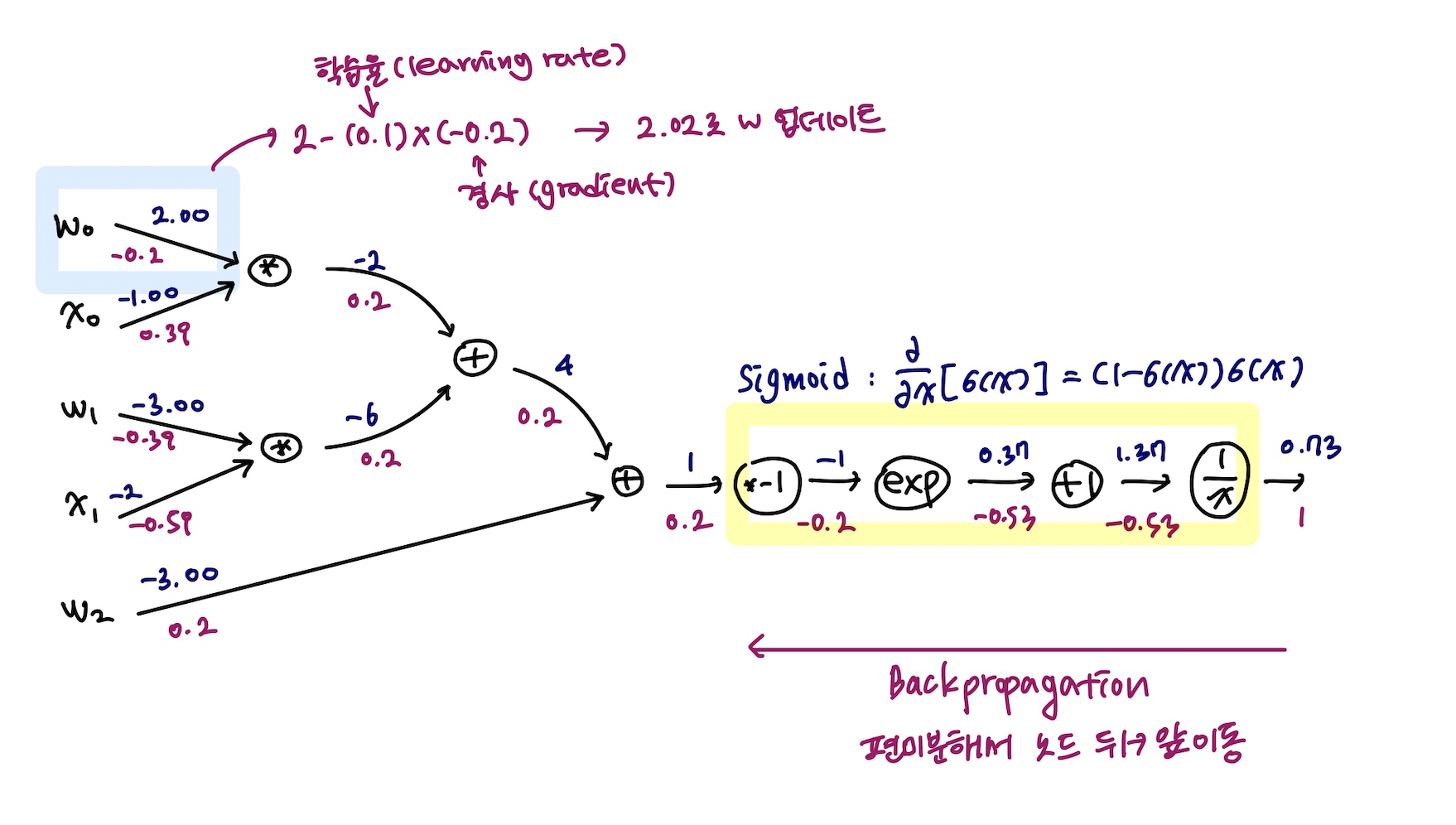
->(1) forward propagation으로 학습을 시작한다.
(2) ground truth 값과 정답함수의 차이를 손실함수를 통해 계산
(3) 이에 따라 최적화의 대상인 w들에 있는 각각 파라미터들에 대해 편미분 값을 구해야 함
(4) 이 편미분한 값을 통해 파라미터를 업데이트를 해야한다. (그러면 gradient descent를 계속 반복할 수 있게 됨)
즉, 손실함수에서 구한 오차값을 통해 편미분값을 구하는 과정은 back propagation 과정이라고 할 수 있다.
3. Logistic regression
어떻게? Back propagation으로 뒤에서부터 앞으로 한 노드씩 편미분을 반복한다. 그러면 제일 첫 노드까지 편미분값을 가져가게 되고, 이 값에 learning rate를 곱한 값을 초기 w값에서부터 빼주면 그게 새로운 w값이 된다.
뒷쪽 sigmoid에 해당하는 부분은 통째로 편미분을 취해서 back propagation을 진행할 수 있다. (시그마 있는 연산식 참고)
< 활성화 함수 >

4. Sigmoid 함수
-> 계단함수를 부드럽게 만든 형태로, -무한대부터 +무한대까지의 값을 전부 0에서 1사이의 값으로 매핑할 수 있다는 장점이 있다.
그러나 반복해서 실행될수록 (뒤에서 앞으로 갈수록) gradient가 0에 수렴해서 학습이 굉장히 느리게 진행된다는 단점이 있음.
-> 그래서 neural network가 학습이 느려지는데 이 문제를 gradient vanishing 문제라고 한다.
5. Tanh 함수
-> sigmoid*2-1
-1~1사이의 값으로 매핑해준다. 학습을 조금 더 빠르게 한다는 장점이 있다. 0~1/2사이에 있는 값에 대해서 마찬가지로 gradient vanishing 문제가 여전히 있다.
6. ReLU 함수
-> Rectified Linear Unit 함수
마이너스 무한대부터 무한대까지, 0보다 작은 쪽은 0으로, 0보다 큰 쪽은 그 값대로 나타내어주는 함수.
0보다 큰 쪽에 대해서는 학습 속도도 빠르고(간단하므로), gradient vanishing 문제가 없다.
그러나 0보다 작은 쪽은 접선의 기울기가 0이고, 아예 gradient가 0이 되어버린다.
7. Batch normalization
: 기본 아이디어 -> 활성화 함수의 그래프를 보면, 기울기가 0인 구간들이 있고 그렇지 않고 기울기가 잘 나오는 구간이 있다.
그 기울기가 잘 나오는 구간에 한해서만 back propagation을 진행시키도록 하는 것이 batch normalization의 목적!
: 활성화함수를 거치기 전에 필터링하는 단계라고 생각하자!
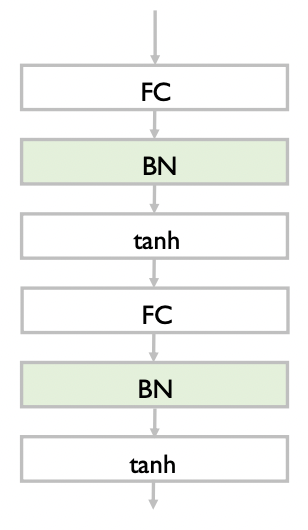
이렇게 진행된다. Fully connected -> batch normalization -> activation function -> 다시 fully connected ..

(1) 먼저, 미니배치 내에 있는 데이터들에 대해 정규화를 진행한다.
-> 이때, 평균은 0 분산은 1로 고정시켜서 정규화를 진행하고, 이 정규화과정을 통해 대략적인 분포를 파악하도록 한다.
-> 그러나, 평균과 분산 값이 어떤 고유한 데이터 자체로서의 의미를 가지고 있는 경우도 있다.
(2) 두번째로, 평균의 조정값을 +B로 추가, 분산의 조정값을 Y*로 추가함으로써 조정을 완성해준다.
