
< Linear regression>
: 모델의 출력이 연속인 값을 갖는다. label이 있는 데이터셋을 사용
1. 선형 모델
: Linear combination으로 이루어진 모델을 linear model이라고 한다.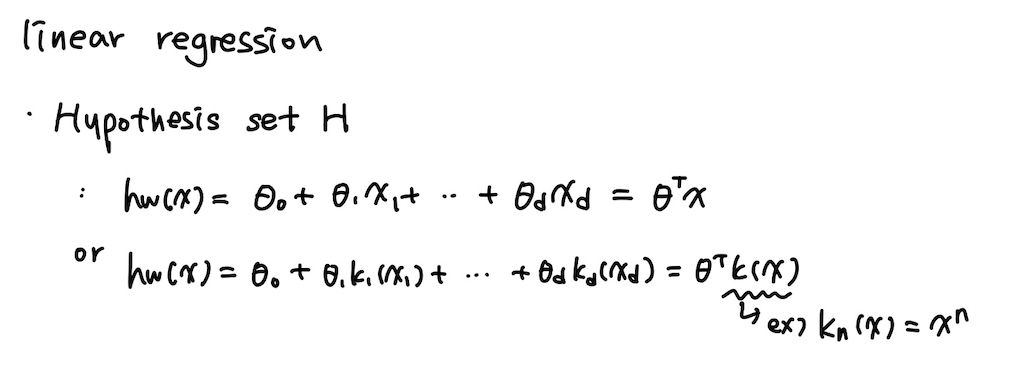
-> 반드시 입력 변수가 선형일 필요는 없다.
-> 간단하고 단순하기 때문에 성능이 높진 않더라도 안정적인 성능을 제공할 수 있다.
-> 모델파라미터와 입력파라미터의 곱의 합으로 표현되며 특히 모델파라미터 값에 따라서 값이 많이 좌우된다.
-> regression/classification에 다 사용할 수 있다.
2. Linear regression. 선형 회귀
: 주어진 입력에 대해 출력과의 선형적인 관계를 추론하는 문제
-> 앞에서 살펴본 supervised learning의 한 종류이기 때문에 입력 x와 출력 y의 쌍으로 구성이 된다. (y는 연속적)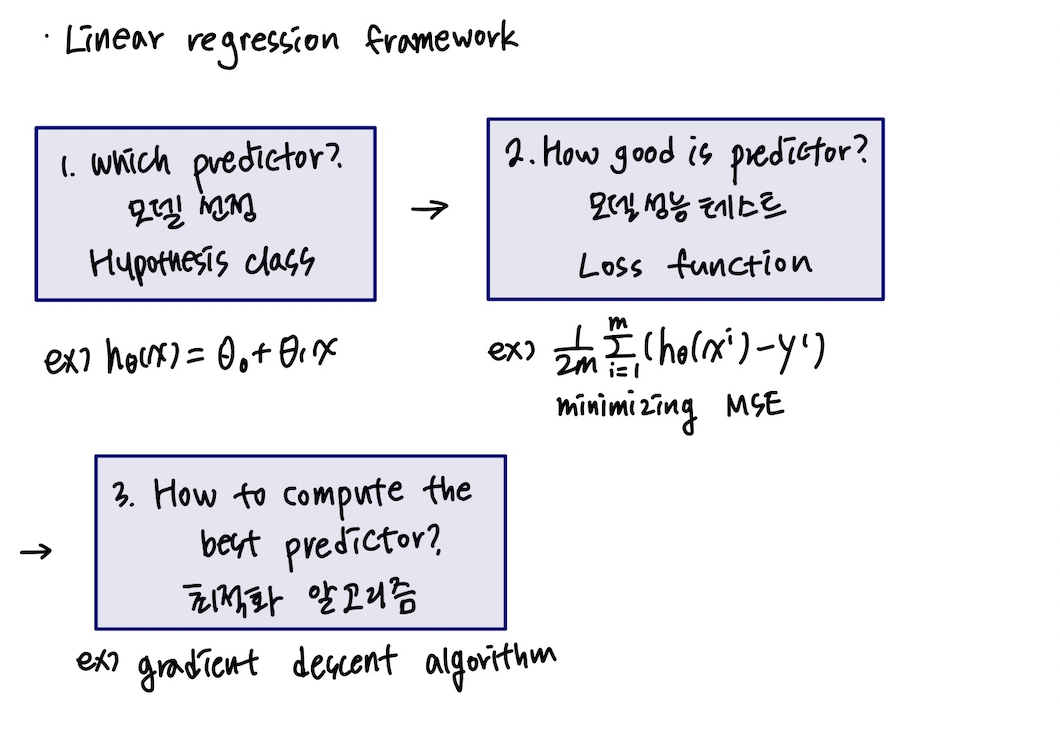
3. Parameter optimization 파라미터 조정
: 가장 마지막 단계. 세타0은 offest이고 세타1은 기울기
이런 모델 파라미터를 최적화하는 작업이 필요함.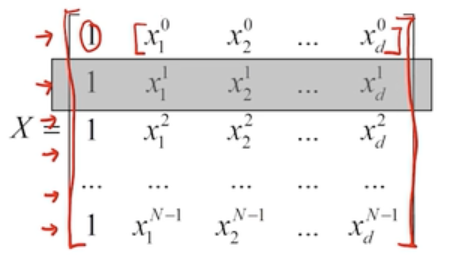
맨 앞의 1 은 offset인 세타0
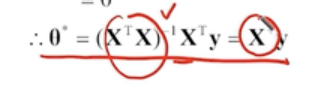
-> 유사 역행렬(pseudo inverse matrix) X^+ 에 y만 곱하면 한번에 해를 구할 수 있다 (normal equation으로 해를 구하는 것)
-> 데이터 샘플의 숫자가 늘어나면 비효율적 (n이 늘어나면 X의 차원이 늘어나기 때문에 X^+를 구하는 데 시간이 오래 걸림)
그래서 사용하는 방법이 gradient descent!
4. Gradient descent : 경사하강법
- Gradient : 함수를 미분하여 얻는 term으로 해당 함수의 변화하는 정도를 표현하는 값
gradient가 0인 지점까지 세타를 바꿔가면서 탐색하는 과정을 경사하강이라고 한다. 함수의 변화도가 가장 큰 방향으로 이동한다.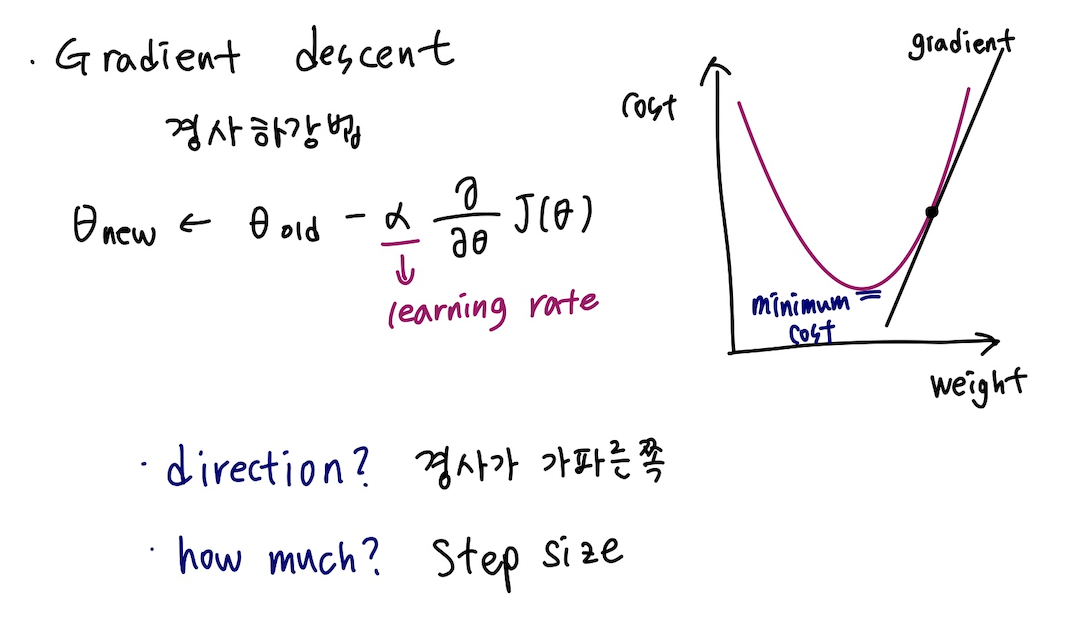
세타 올드 위에 있는 값이 step size라고 한다.
알파가 너무 크다 : 0인 지점을 놓치지 쉽다.
알파가 너무 작다 : 수렴하는 데 시간이 너무 오래 걸린다.
변화도가 가장 가파른 방향으로 업데이트한다.
5. Global optimum, local optimum
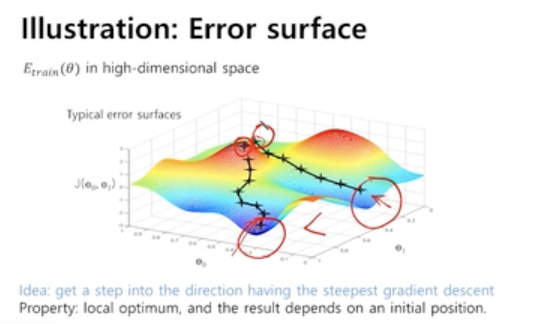
현재 지점에서 가장 가파른 변화도를 보고 움직이기 때문에 내가 이동한 방향이 최적화된 포인트가 아니게 될 가능성이 있다.
지역적으로 최소인 지점과 전체 영역에서의 최소인 지점이 다를 수 있다.
6. Linear regression
실행 순서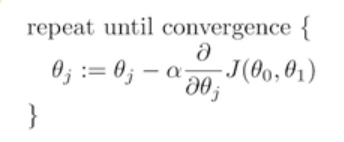
- 최적화하고자 하는 loss function/objective function을 세운다
- 알고리즘 수행에 필요한 파라미터(ex. Alpha)를 사전에 설정한다. ( 사전에 설정하는 파라미터를 하이퍼 파라미터라고 하고, 이 하이퍼 파라미터 값은 항상 양의 값을 가진다. 학습하면서 바뀌는 파라미터인 세타는 learnable parameter라고 한다.)
- 수렴할 때까지 러너블 파라미터를 계속 업데이트한다.
7. Gradient descent vs Normal equation
- 경사하강법은 여러번의 반복 수행을 통해 해를 얻어 나간다.
- Normal equation은 한방에 해를 얻지만 x^+를 구하기 위해 n이 크다면 cost가 크다.
* 퀴즈
- 선형회귀에서 해는 인풋 피쳐에 대해 해석 가능한가? Yes. 입력 피쳐와 가중치에 따라 최종 아웃풋이 달라지므로.
- 선형회귀에서 hypothesis는 linear form이 아니어도 된다.
