
지도학습의 목적은 target function f를 approximation하는 hypothesis h를 학습하는 것!
< Classification >
(1) model 의 출력값이 discrete
(2) label이 있는 데이터를 사용하게 됨.
(3) Linear regression와 같이 linear model을 사용한다.

(입력 피쳐와 해당파라미터 셋이 Linear combination 되어 있는 형태)
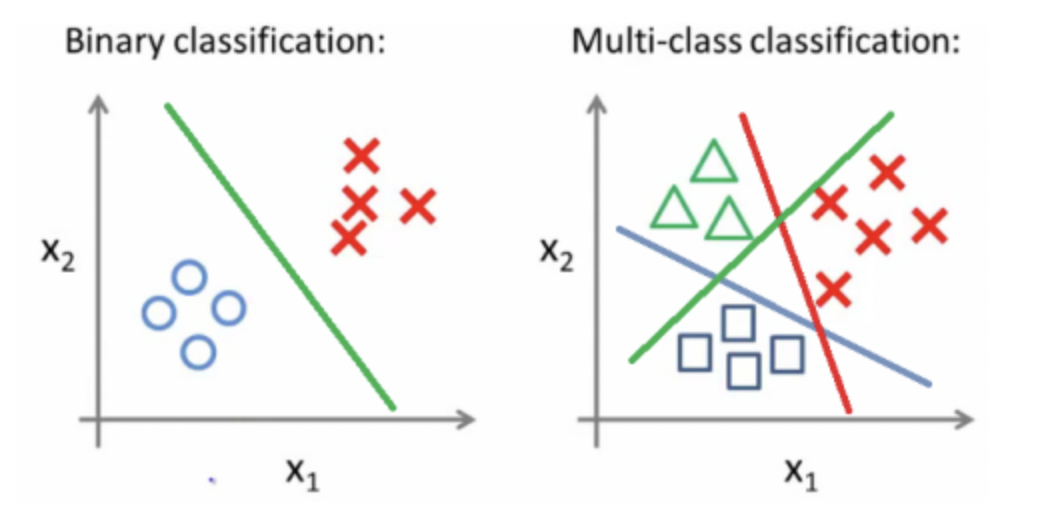
1. Binary classification
-> 2차원 데이터
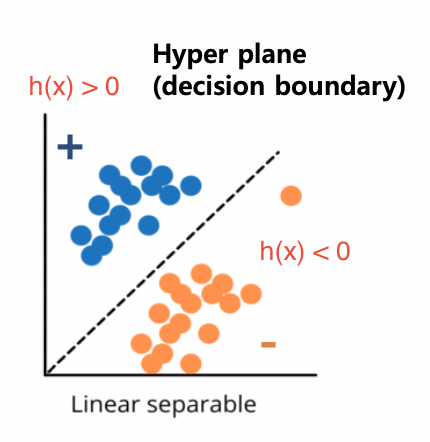
파란색 : positive sample
노란색 : negative sample.
Hyper plane : h(x) = 0인 식
목적 : 구분선인 hyper plane을 구해서 positive sample, negative sample을 구분하는 것
2. Multiclass classification
-> 입력 신호 공간에서 Hyper plane이 다수 존재하는 경우
- 어떤 predictor를 사용할 것인가?
- Loss function으로 predictor 성능 판단
- 최적화 작업

3. Linear classification model
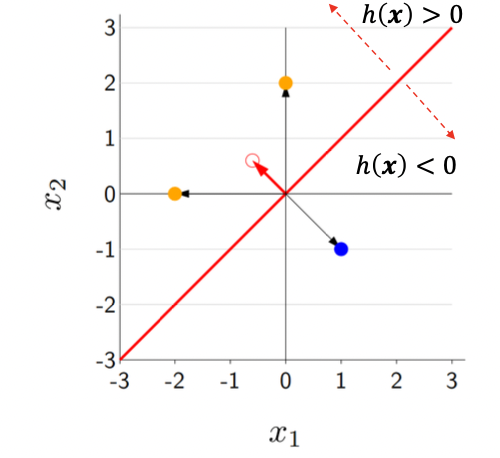
빨간색 구분 선 -> 일차선형함수로 구성된 hypothesis h(x)
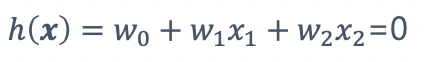
이 함수의 양과 음을 판별하는 sign함수를 씌워서 최종 h(x)를 구한다.
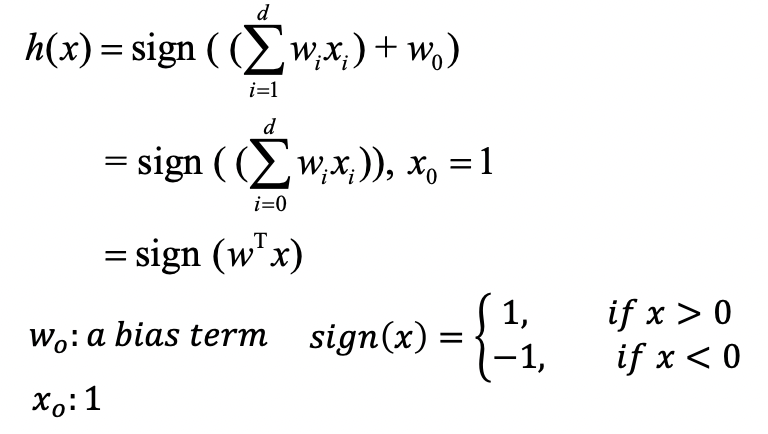
요약 :
(1) 입력 변수와 파라미터의 곱으로 score 계산
-> W0: bias/offset
(2) 그 출력에 sign 함수 적용
-> 내부의 값이 음이면 -1

함수에 들어가는 입력 score(W^T*x)이 커지게되면 h(x)(hyper plane)로부터 좌표까지의 거리가 멀어진다는 것을 알 수 있음
4. Score & margin
Score : 모델이 얼마나 잘 예측하는지(confident)를 측정한 지표
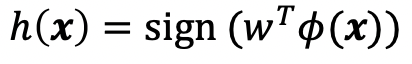
Margin : score에 target label y를 곱한 값
-> y는 1 또는 -1, 정답의 유무를 나타낸다.
-> y와 score를 곱하면 모델이 정확한 출력을 했는지 아닌지의 여부를 간단히 확인할 수 있다.
5. Error functions
(1) Zero-one loss : logic이 맞으면 1, 아니면 0
-> gradient descent에 적용하려면 손실함수의 편미분값을 구해야하는데, 계단함수의 경우에는 경사가 0이 된다.
즉 학습이 불가능한 경우가 생긴다는 단점이 있다.
(2) Hinge loss : 미분하면 gradient가 0이 되는 경우에 대한 해결책.
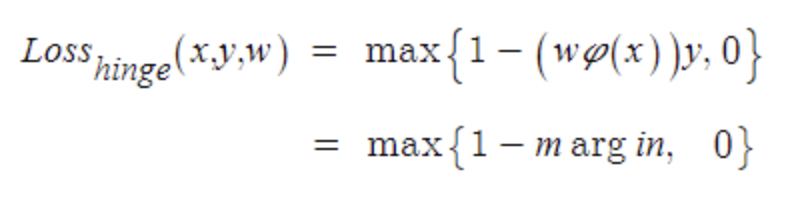
margin값과 0중에 큰 값을 선택해서 -가 되지 않도록 한다. 즉, 모델이 정답을 잘 맞추고 있다면 margin>0, 최종값은 음수가 되고,학습이 잘 이루어지지 않는 경우에는 (margin<0) 0으로 세팅함으로써 양수값을 가져 loss가 발생한다.
(3) cross-entropy loss : classification 학습에 가장 많이 사용되는 loss function
-> K-L divergence: 서로 다른 두 함수(pmf)의 차이
= 크로스엔트로피 역시 서로 다른 pmf가 서로 유사한지 아닌지에 따라 에러의 정도가 달라진다.
(서로 많이 다르면 loss가 올라간다)
-> 그러나 우리가 지금까지 앞서 계산한 모델의 score값은 실수값이다.
크로스엔트로피 값은 확률값으로 비교를 하는데 어떻게 하면 실수인 score값을 확률값으로 매핑할 수 있을까?
sigmoid
-> cross-entropy loss 에서 𝑤𝑇𝜙(𝒙) 를 sigmoid 함수에 넣으면 score값을 0~1사이의 확률값으로 매핑할 수 있다.
𝜎(𝑧) = 1 / 1+𝑒−𝑧
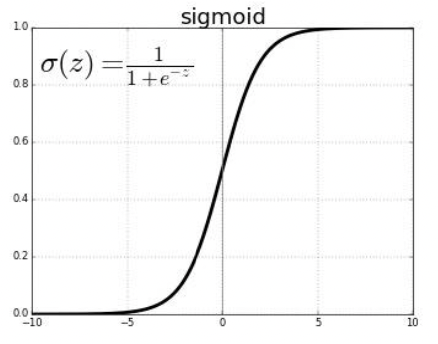
두개의 다른 함수 P와 Q가 있다고 할 때 (하나는 정답함수, 하나는 예측모델), 각각을 시그모이드 함수를 거쳐 확률값으로 변환한 다음

이 식에 맞추어 넣어주면 두 함수의 차이를 계산할 수 있다. (Loss function)
-> gradient descent로 optimizing
: 가중치를 초기화한 다음, 그 시점에서의 경사를 계산하고, 방향을 결정한다음 가중치를 업데이트한다. -> 수렴할 때까지 반복
6. Multiclass classification - One vs All
: binary classification을 multiclass classification 문제로 확장해서 풀이하는 방식.
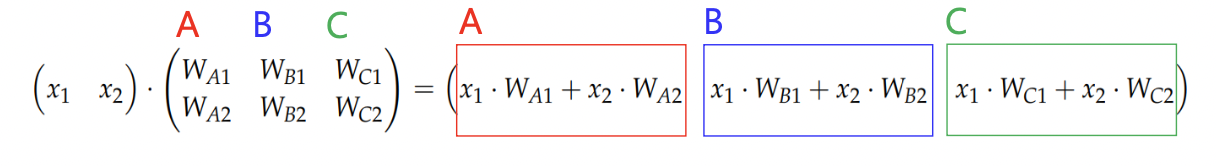
7. Linear classification 의 장점
-> 간단하다. 쉽게 구현/테스트가 가능하다. 가장 처음에 시도하기 적합한 형태.
-> 해석 가능성이 뛰어나다
: 각 요소별로 요소가 1 단위로 증가할 때마다 score가 어떻게 변화하게 되는지 추정함으로써 해석 가능성을 제공한다.
* Quiz
- Linear classification model에서 hyperplane은 훈련 데이터를 분류하기 위한 decision boundary로서 사용된다.
-> true. - Cross-entropy loss 는 두가지 실수의 값 사이의 차이 또는 오차를 나타낸다.
-> false. 값이 아니라 함수(pmf)의 차이를 나타낸다. - Binary linear classifier는 multiclass linear classifier로 확장이 가능하다
-> true. 마지막에 배운 one vs all
