이번 시간에는 hierarchical clustering, 즉 계층적 군집화에 대해 알아볼거에요. 여태까지 다루었던 여러 알고리즘처럼 이 알고리즘 또한 데이터들을 분류해주는 알고리즘이랍니다.
알고리즘 개요
개념
hierarchical clustering 알고리즘은 개체들을 가까운 집단부터 순차적이고 계층적으로 차근차근 묶어나가는 방식을 사용합니다. 즉 군집을 형성을 하는데 있어서 매 단계에서 최적해(local minimum)을 찾아가는 것입니다. 그러나 여기서 주의해야 할 점은 이 과정이 전역적 최적해(global minimum)으로 이어지지 않는다는 점입니다.
위의 방식으로 군집을 형성하기 때문에 dendogram을 통해 데이터를 시각화하기에도 용의합니다. 아래 그림이 이의 예시입니다.
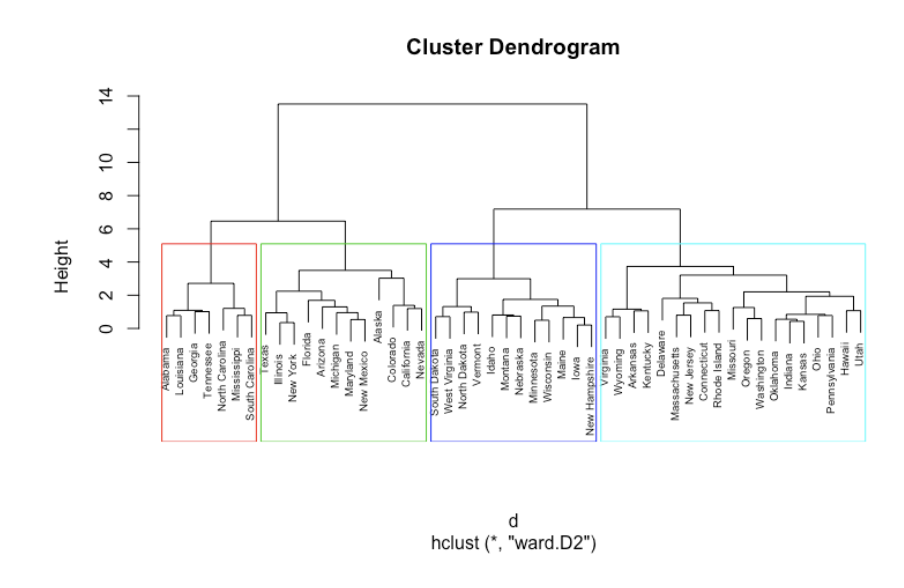
알고리즘 학습과정
이 알고리즘이 수행되기 위해서는 모든 개체들간의 거리에 대한 유사도가 계산되어야 합니다. 이때, 거리가 계산되는 방식에는 대게 유클리디안 거리(euclidean distance)가 사용됩니다.
거리 계산에 사용되는 방식(metric)은 학습의 영역이나 본질에 따라 결정되어야 한다. 예를 들어 도시의 범죄 현장을 묶는 과정에서는 유클리디안 거리보다 블록(block)을 계산하는 manhattan distance가 더 적절할 수도 있는 것이다. 그럼에도 대게 유클리디안 거리가 많은 상황에 부합하기에 이 방식이 자주 사용된다.
거리가 계산되었으면 다음과 같은 방식으로 학습이 진행됩니다. 아래의 데이터는 4개의 개체들을 계산한 거리 행렬입니다.
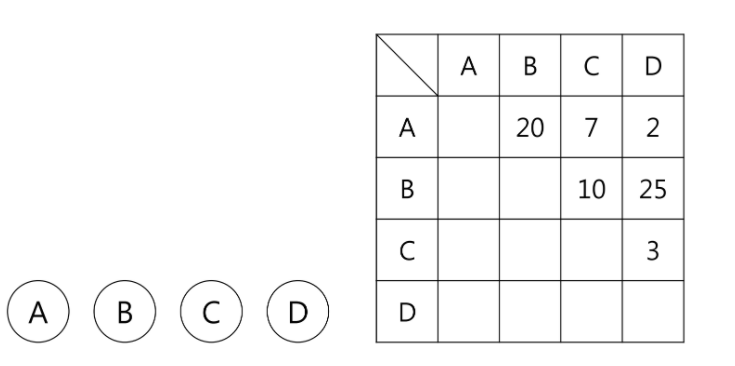
가장 거리가 가까운 개체들을 묶으면 아래와 같습니다.
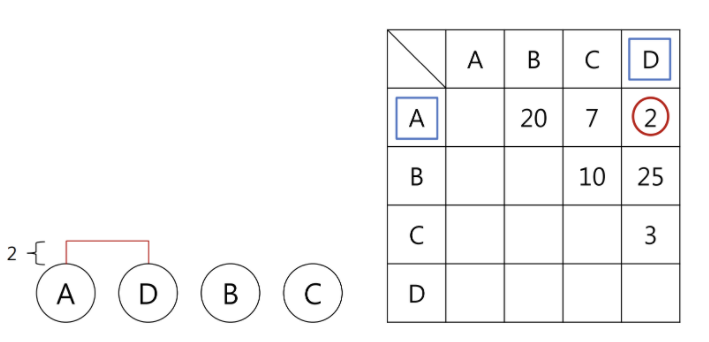
자 그럼 단계에서는 AD 군집과 다른 개체들 간의 거리를 계산해주어야 합니다. 이때 여기서 다음과 같은 물음이 생길 수 밖에 없습니다.
군집과 개체 간의 거리는 어떻게 구하지..?
개체-군집 거리를 계산하는 방식에는 아래 그림과 같이 다양한 방식이 존재합니다.
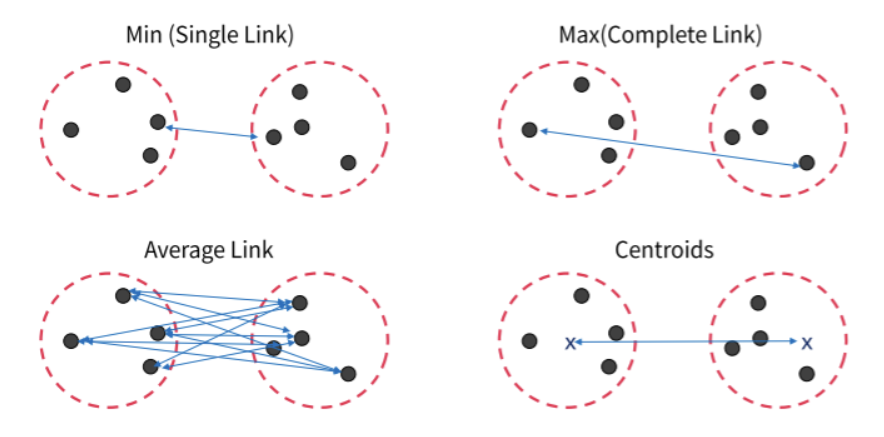
그리고 추가적으로 Ward's method가 존재합니다. 이 방법은 두 개의 군집이 병합되었을 때 증가되는 변동성의 양을 기준으로 계산하는 방식입니다. 아래 그림에서 ward's method를 따르면 왼쪽이 아닌 오른쪽의 방식으로 개체들을 분류하게 될 것을 알 수 있습니다.

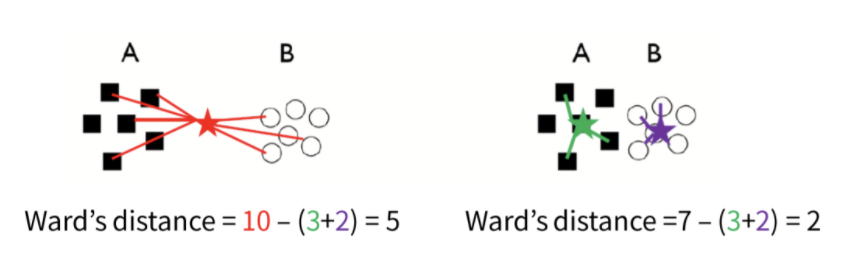
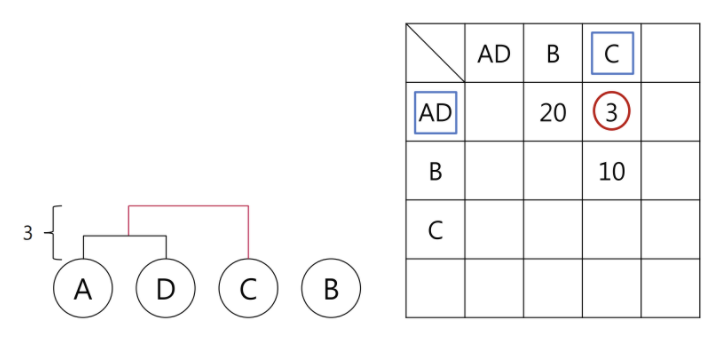
그럼 다시 돌아와서 위의 5가지 방식 중 하나를 선택했다고 합시다. 그랬더니 AD와 C가 가장 인접합니다. 그러니 이 둘을 묶어줍니다.
이 과정을 한번 더 적용하면 아래와 같습니다.
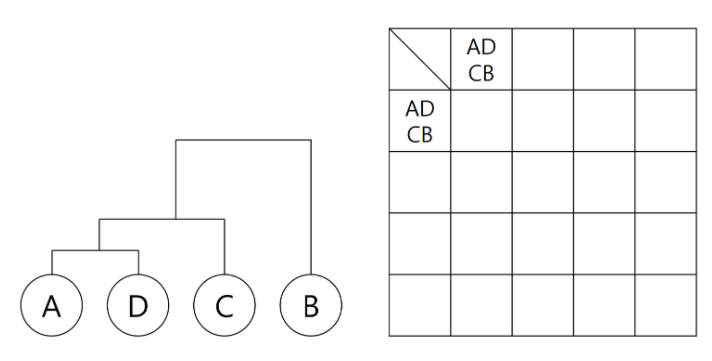
더 이상의 분석 대상치가 존재하지 않기에 여기서 학습을 종료합니다.
실전 적용
자 그럼 간단한 예시에 적용해보자.
우선 필요한 method를 불러오자.

그리고 우리가 사용할 데이터들을 만들어주자.

이 데이터들을 시각화 해주자. 이 시각화된 정보를 바탕으로 아래 hierarchical tree를 보면 tree가 만들어진 과정을 이해하는데 도움이 될 것이다.
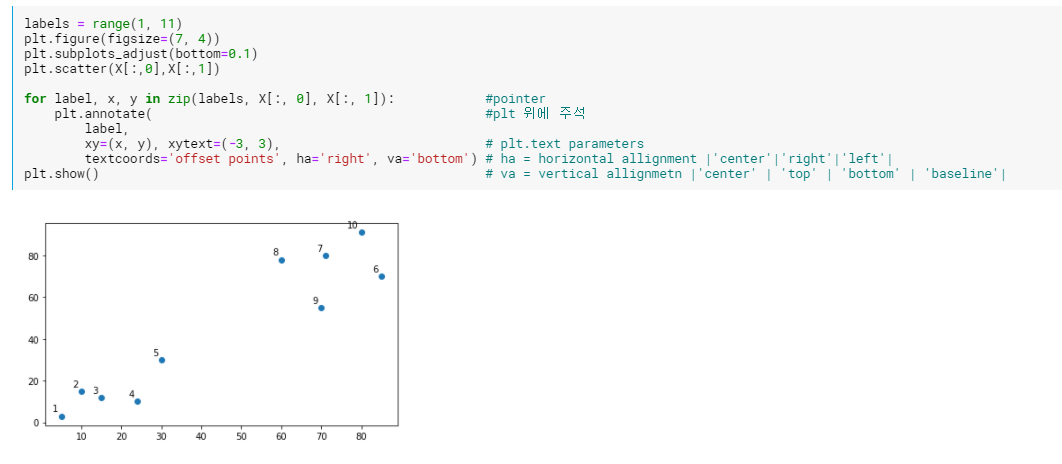
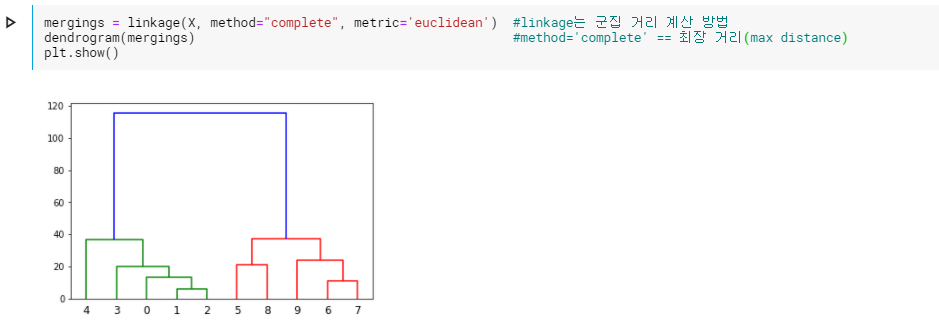
scipy를 이용해서 아래와 같이 hierarchical tree를 만들 수 있다.
출처
알고리즘 개요
https://ratsgo.github.io/machine%20learning/2017/04/18/HC/
https://todayisbetterthanyesterday.tistory.com/59
https://www.displayr.com/what-is-hierarchical-clustering/
실전 적용
https://todayisbetterthanyesterday.tistory.com/61
https://www.kaggle.com/maithiltandel/kmeans-hierarchical-clustering/data
https://www.kaggle.com/alexhur/hierarchical-clustering