SVM

허민석·2021년 2월 19일

Machine Learning

목록 보기

7/7

저번 포스팅에 이어 이번에는 support vector machine(SVM)에 대해 알아보도록 할게요. SVM은 역사가 오래되었답니다. 무려 1963에 개발된 머신러닝 기법이랍니다. 역사가 깊은 만큼 수학적인 내용도 꽤 많습니다. 그러나 그 내용이 매우 복잡하고 살아있는 코코넛인 제가 이해조차하지 못하는 내용이 많았기에 이번 포스트에서는 개념과 sklearn을 이용한 간단한 실습에 대해 알아보도록 할게요.

모델 개요

개념

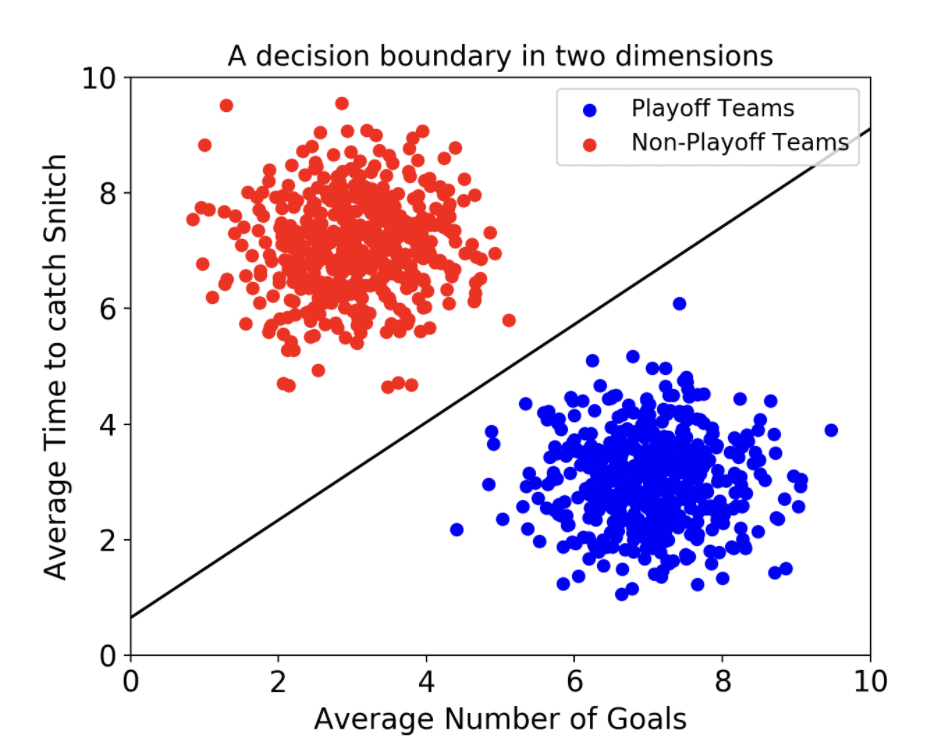
SVM은 머신러닝에서 개체들을 분류하는데 사용되는 모델입니다. 개체들을 결정 경계(decision boundary)라는 기준 선으로 분류하는데요 이때 이 boundary를 결정하는 과정이 이 알고리즘의 핵심이랍니다. 아래있는 사진에서 그어져 있는 직선이 boundary이고 이는 사람이 봤을 때 꽤 직관적입니다.
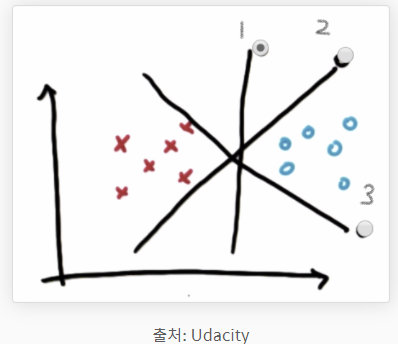위의 그림에서 어느 선이 데이터들을 가장 적합하게 분류한 것일까요? 맞아요, 1번 선이에요. 이렇듯 매우 직관적이지만, 수학적으로는 꽤 복잡한 과정을 거쳐야합니다. 그러니 저희는 실전적용에 필요한 개념들에 대해서만 다루어보도록 할게요.

margin

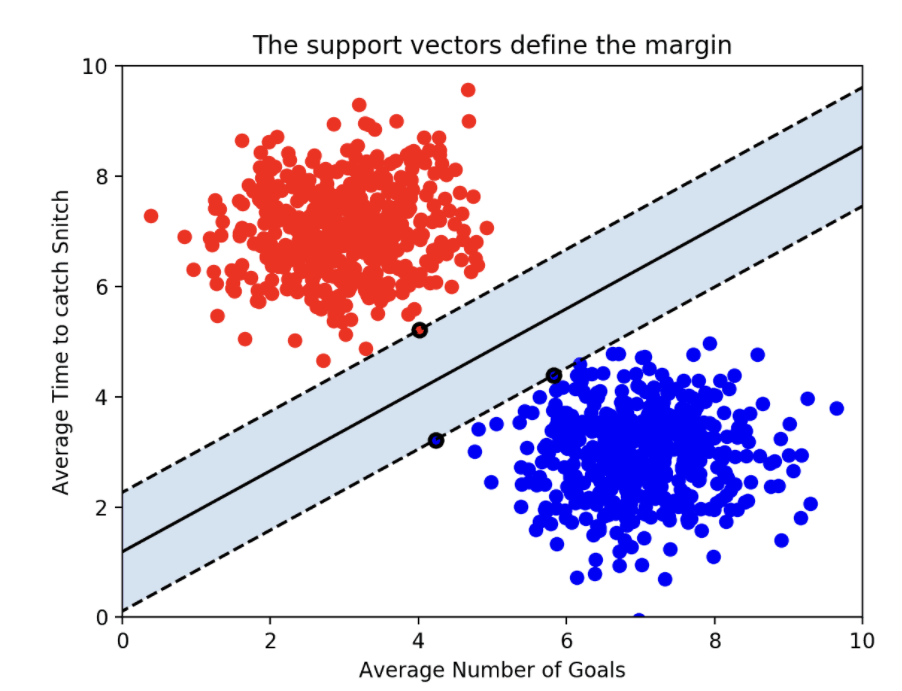SVM에서 support vector이 무엇인지 궁금해 하실꺼라 생각합니다. 위의 그림을 보았을 때, 빨간점 1개와 파란점 2개에 점선 두 개가 지나가고 있는 것을 확인할 수 있는데요 이때 이 점들이 support vector입니다. 그리고 boundary는 이 서포트 벡터와의 거리가 최대입니다. 즉, 최적의 boundary는 margin을 최대화하는 선입니다. margin이 바로 서포트 벡터와 boundary간의 거리입니다.

robustness

robustness는 margin이 최대화될때 최대값을 지닙니다. robust는 형용사로 건장한, 튼튼한의 의미를 지니는데요 data science에서는 아웃라이어의 영향을 받지 않고 중앙값을 잘 나타내는 값을 robust하다고 합니다. 예시를 통해 설명을 덧붙히겠습니다.

1,2,3,4,5 이렇게 다섯 개의 데이터가 있을때 평균은 3이고 중앙값 또한 3입니다.
그러나 1,2,3,4,100 이렇게 데이터셋이 바뀌면 평균은 22가 되나 중앙값은 여전히 3입니다. 평균은 아웃라이어(outlier)의 영향을 받아 크게 바뀌었지만, 중앙값은 3으로 영향을 받지 않았습니다. 이때 중앙값을 robust하다고 말하고 SVM에서 decision boundary는 그러한 속성을 지녀야 합니다.

kernel trick

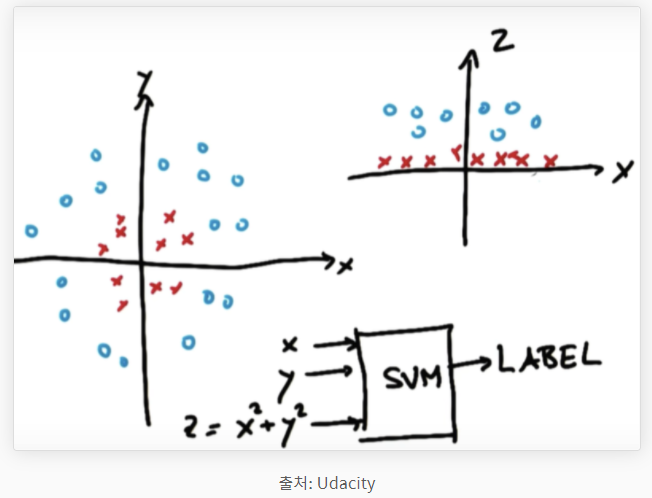왼쪽의 그래프에서 볼 수 있듯이 빨간점과 파란점을 직선으로 구분하기는 어려워 보입니다. 이때 사용되는 방식이 kernel trick입니다. 저차원의 데이터들을 고차원으로 옮겨 구분한 후에 다시 저차원에 적용시키는 방식입니다. 위에서는 왼쪽의 데이터에 z = x^2 + y^2를 적용하여 오른쪽의 그래프로 차원을 향상시킨 것을 확인 할 수 있습니다. 그렇게 하면 아래와 같이 "it can be linearyly separable"하다는 결론을 내릴 수 있습니다.

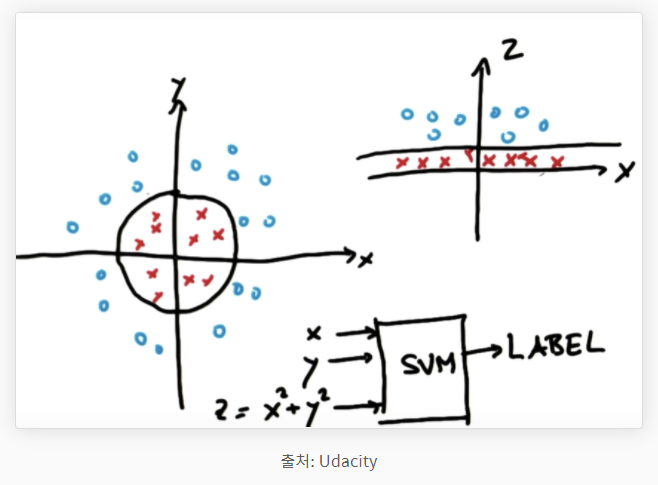
여기로 들어오시면 이 과정을 시각화된 영상을 통해 확인할 수 있습니다.

parameters

scikit learn 공식 사이트에서 skelarn.svm.svc에 들어가시면 실전적용에 필요한 parameters에 대해 알 수 있는데요, 여기서 간단하게 대표적인 parameter들이 어떤 역할을 하는지에 대해 알아보도록 하겠습니다.

kernel

kernel parameter는 decision boundary의 모양을 결정해줍니다. linear, polynomial, sigmoid, rb 등 중에서 선택하면 됩니다. 이때 linear kernel에 대해서는 gamma값이 존재하지 않습니다. (default == 1.0)

C

C : Controls tradeoff detween smooth decision boundary and classfying training points correctly
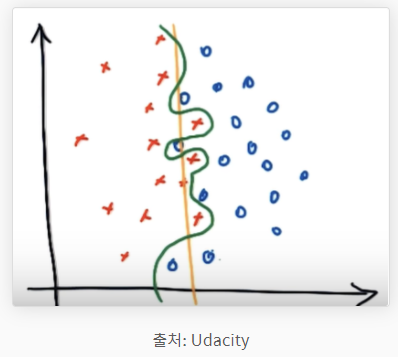위 그림에서 초록색 구분선은 C가 큰 decision boundary이고 주황색은 C가 작은 decision boundary입니다. C가 크면 decision boundary는 굴곡져지고 C가 작으면 smooth 해집니다. C가 작을수록 margin이 커집니다.

gamma(γ)

Gamma: Defines how far the influence of a single training point reaches
여기서 reach는 데이터가 decision boundary에 영향을 주는 범위라고 보면 됩니다. 그림을 보면 이해하는데 도움이 될 것입니다. 아래의 데이터셋을 예시로 gamma값을 다양하게 해보겠습니다.

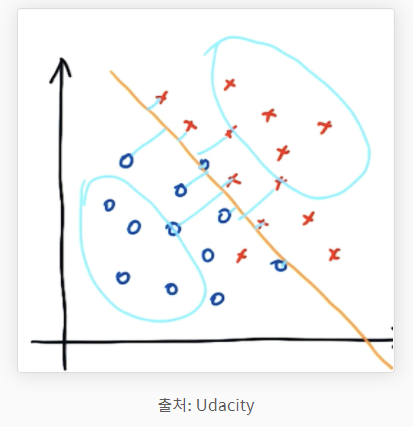
gamma가 클 때
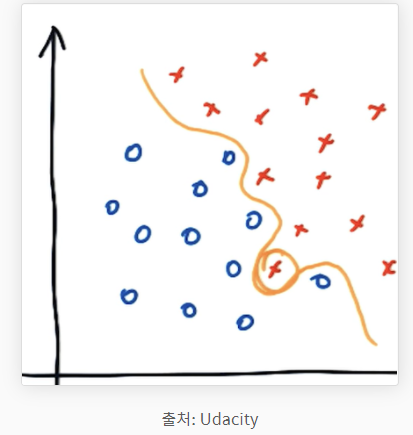gamma가 크면 reach가 좁아집니다. 즉, boundary decision에 영향을 주는 데이터들이 줄어들기 때문에 decision boundary는 local한 특성을 지니게 되고 굴곡이 심해지게 됩니다.

gamma가 작을 때
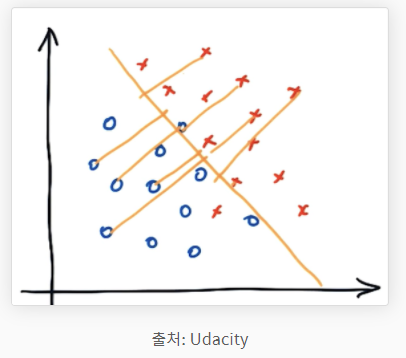gamma가 작은 경우 reach가 크기 때문에 boundary decision은 global한 특성을 지니게 됩니다. 따라서 굴곡이 매우 적습니다.

실전적용

실습은 매우 유명한 heart disease UCI 데이터셋을 사용해서 적용해보도록 하겠습니다.
우선 제가 사용한 라이브러리를 보여드리겠습니다.

그리고 아래와 같이 데이터들을 불러와줍니다.

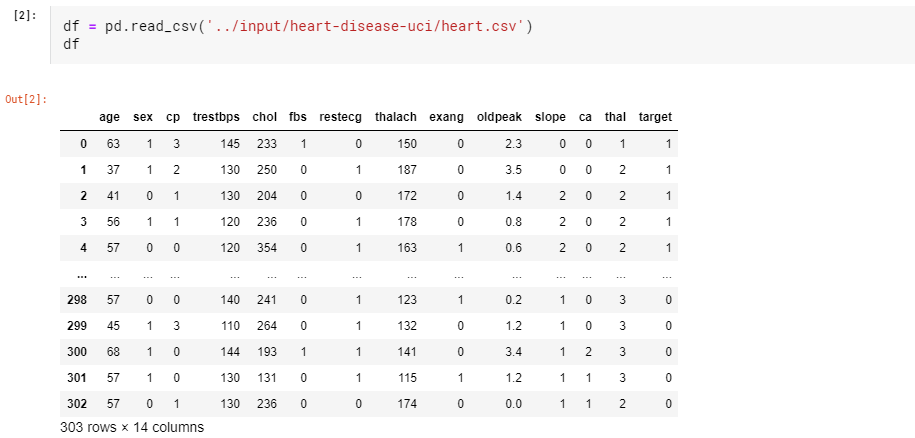
그 다음 이 데이터들을 data와 heart disease의 유무를 나타내는 target dataframe으로 나누어줄게요.

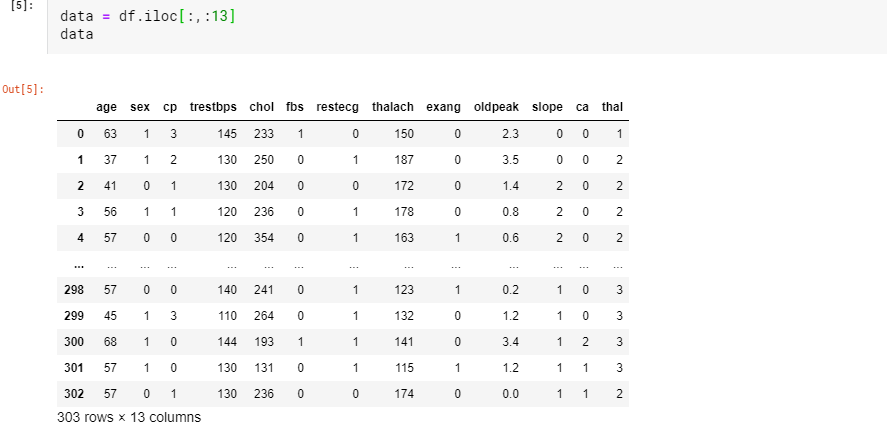
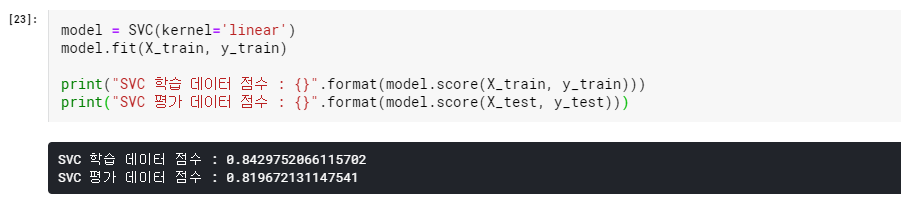
그리고 이 데이터들을 사용해서 데이터들을 train_test_split을 이용해 나누어주고 SVM 중 분류 모델에 해당하는 SVC에 학습시켜줍니다.

생각보다 정확도가 낮습니다. 이럴때는 데이터들을 정규화시켜주어야 합니다. Standard Scaler를 이용해서 데이터들을 정규화시켜주겠습니다.
그리고 이 정규화된 데이터셋으로 다시 모델을 학습시키면 수행능력이 향상한 것을 확인할 수 있습니다.

사실 이미지로도 보여드리고는 싶으나 생각보다 그래프가 예쁘게 나타나지 않아서 그냥 이렇게 마무리하도록 하겠습니다.

사용된 노트북은 출처란에 기재되어있습니다.