Scaled Exponential Linear Unit (SELU)

Introduction

The Scaled Exponential Linear Unit (SELU) is an activation function used in neural networks that automatically induces self-normalizing properties in feedforward neural networks. Introduced by Klambauer et al. in 2017, the SELU function is designed to lead to a mean and variance of the outputs close to zero and one, respectively, across network layers during training. This characteristic can improve the training speed and convergence properties of deep neural networks.

Background and Theory

The SELU activation function is an advanced variant of the traditional exponential linear unit (ELU) and introduces a scaling factor to the output. The function is part of a family of activation functions that includes the rectified linear unit (ReLU) and its variants. SELU is particularly noteworthy for its self-normalizing properties, which help maintain a mean of zero and variance of one across the network layers, assuming the weights are initialized appropriately (e.g., using LeCun normal initialization).

Mathematical Foundations

The SELU function is mathematically defined as follows:

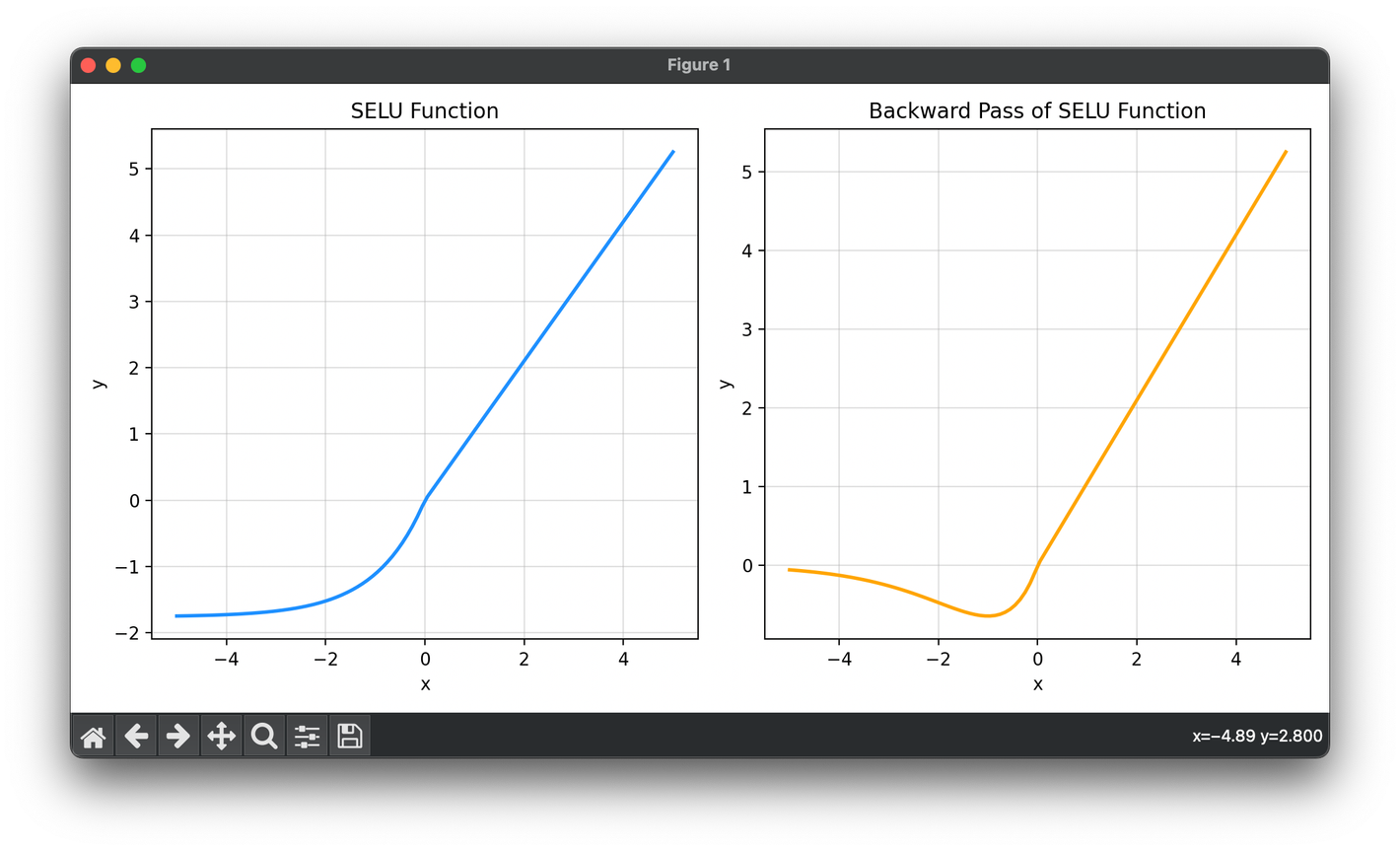
where $\lambda$ is a predefined scaling parameter, and $\alpha$ is another predefined parameter typically derived from fixed-point equations that ensure self-normalization. Specifically, $\alpha$ and $\lambda$ are defined to ensure that the mean and variance remain invariant across layers, which are crucial for deep neural networks to avoid the vanishing or exploding gradient problems.

Procedural Steps

1. Initialization: Initialize the network weights using a distribution that supports SELU's self-normalizing property, such as the LeCun normal initialization.

2. Forward Pass Calculation: Apply the SELU function as defined above to each input $x$ in the layer during the forward pass of the network training.

3. Backward Pass Calculation: During the backward pass, compute the gradient of the SELU function to be used in the weight update step. The derivative of SELU is:

   $\text{SELU}^\prime(x) = \lambda \left\{ \begin{array}{ll} 1 & \text{if } x > 0, \\ \alpha e^x & \text{if } x \leq 0. \end{array} \right.$

Applications

SELU has found applications in various neural network architectures, particularly in those that are deep and prone to issues related to gradient propagation:

• Deep Feedforward Networks: Where maintaining stable dynamics in deeper layers is crucial.
• Autoencoders: Where the preservation of variance and mean across layers can help in better encoding and decoding.
• Generative Models: Stability in gradient flow aids in training deeper generative models.

Strengths and Limitations

Strengths

• Self-normalization: Promotes a stable and normalized internal state across layers, which enhances training efficiency and reduces the need for external normalization techniques.
• Improved Convergence: Helps in achieving faster convergence in training deep neural networks.

Limitations

• Parameter Sensitivity: The performance of SELU is sensitive to the correct initialization and the specific values of $\alpha$ and $\lambda$.
• Incompatibility: Not all architectures benefit equally from SELU, and it may not be compatible with other regularization or normalization techniques.

Advanced Topics

Impact on Learning Dynamics

The self-normalizing property of SELU significantly influences learning dynamics by maintaining normalized activations across the network, which is particularly beneficial in deep architectures where depth can affect learning and gradient propagation.

Conclusion

The SELU activation function is a powerful tool in the neural network toolkit, particularly for deep learning applications where maintaining activation variances and means across network layers is challenging. Its self-normalizing properties make it a distinctive choice for scenarios where fast convergence and training stability are critical.

References

1. Klambauer, Günter, et al. "Self-Normalizing Neural Networks." Advances in Neural Information Processing Systems, 2017.
2. LeCun, Yann, et al. "Efficient BackProp." Neural Networks: Tricks of the Trade, Springer, 2012, pp. 9-48.