Softplus

Introduction

The Softplus activation function is a smooth, nonlinear function used in neural networks as an alternative to the commonly used Rectified Linear Unit (ReLU). Introduced to provide a continuously differentiable curve that closely approximates the ReLU function, Softplus addresses some of the limitations of ReLU, such as the non-differentiability at zero and the dying ReLU problem where neurons permanently output zeros.

Background and Theory

Softplus is part of the family of activation functions designed to introduce non-linearity into the neural networks while maintaining differentiability everywhere. The primary purpose of using Softplus is to have a gradient that does not vanish abruptly, which can help in maintaining a healthier gradient flow during backpropagation.

Mathematical Foundations

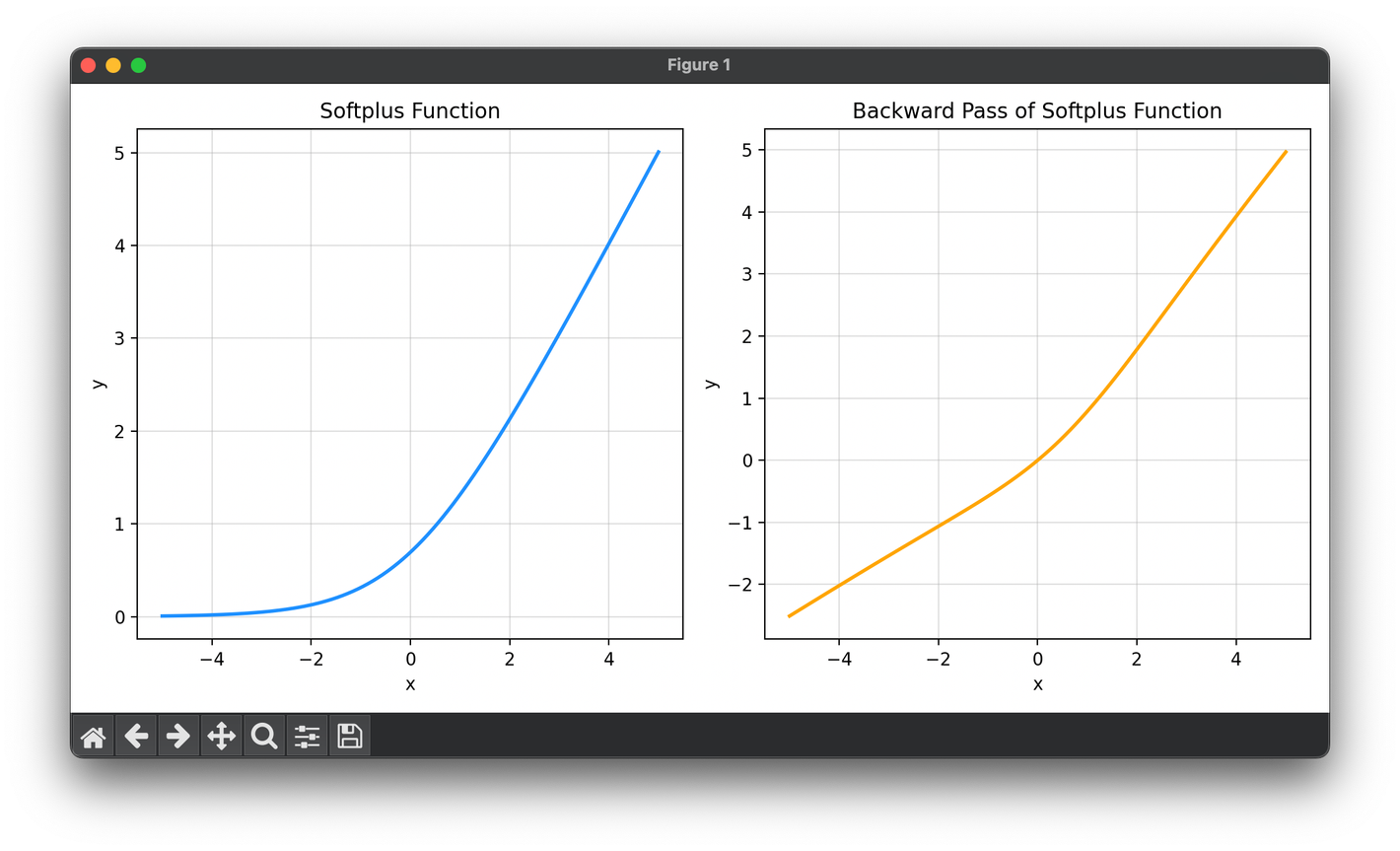
The Softplus function is mathematically defined as follows:

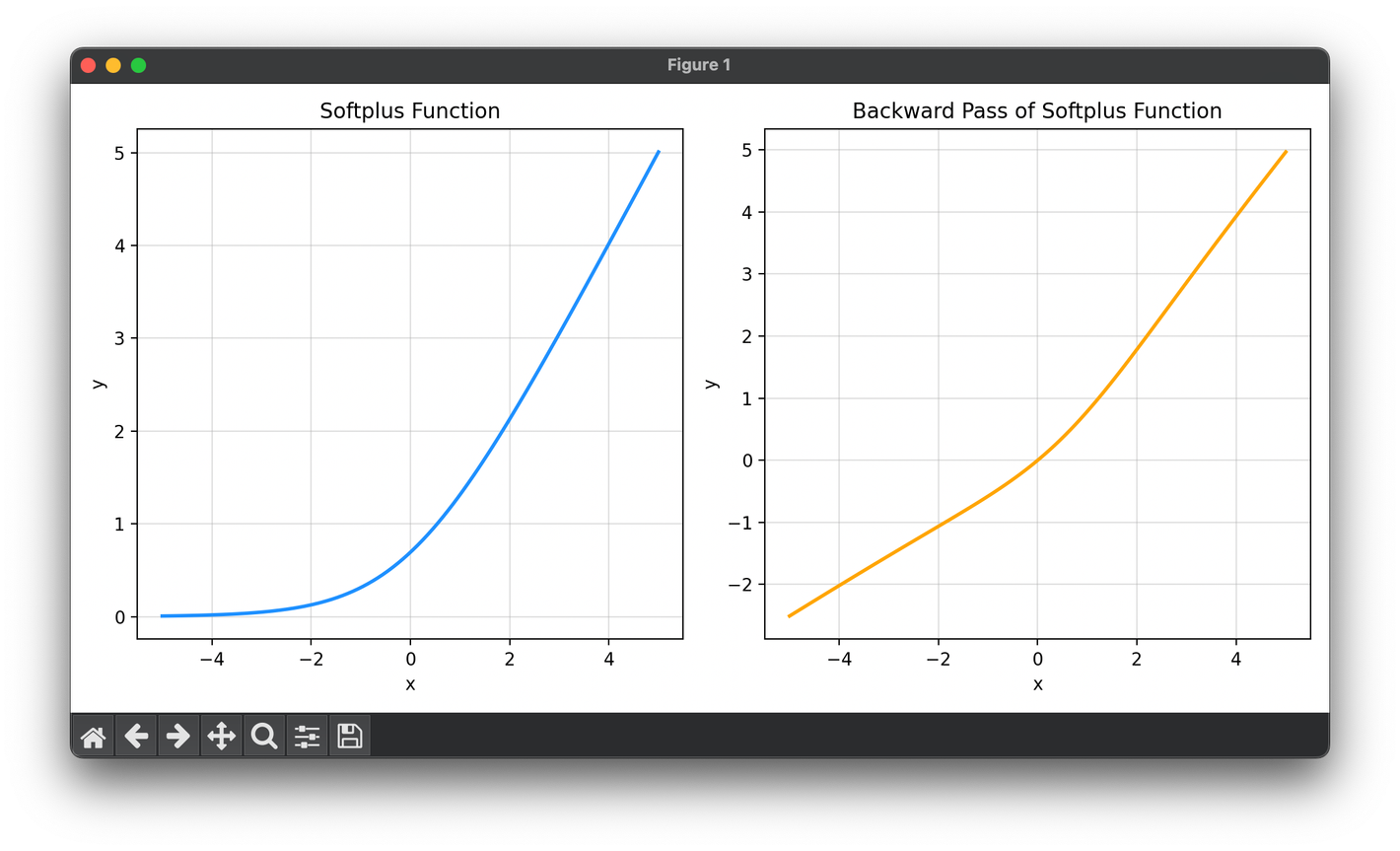
This function provides a smooth approximation to the ReLU function, which is defined as $\max(0, x)$. Unlike ReLU, Softplus is differentiable at every point, including at $x=0$, where the ReLU's derivative is undefined.

Procedural Steps

1. Computation: For each input $x$ to the neuron, compute the Softplus function value using the formula $\log(1 + e^x)$.

2. Differentiation: The derivative of the Softplus function, necessary for the backpropagation algorithm, is given by the logistic or sigmoid function:

   $\frac{d}{dx} \text{Softplus}(x) = \frac{1}{1 + e^{-x}}$

   This derivative ensures a smooth gradient flow, avoiding the issues of dying gradients seen with ReLU in some cases.

Applications

Softplus is used in various neural network configurations where smooth gradients are preferable:

• Regression Models: Especially in outputs where a smooth transition between activation levels is beneficial.
• Probabilistic Models: Where a soft, smooth activation is required, for example, in variational autoencoders.
• Deep Learning: In layers where non-linear, smooth activation functions might help avoid issues related to non-differentiability.

Strengths and Limitations

Strengths

• Smoothness: Softplus is continuously differentiable, which makes it useful in optimization scenarios where smoothness is desired.
• Avoidance of Dead Neurons: Unlike ReLU, Softplus does not suffer from the issue of dead neurons as it does not output zero for negative inputs, which can help in maintaining active neuron states throughout training.

Limitations

• Computational Intensity: The computation of the exponential function can be more costly compared to the simple max operation in ReLU.
• Saturated Gradients: For very large values of $x$, the gradient can become very small (though not exactly zero), potentially leading to slow learning during those phases.

Advanced Topics

Comparison with Other Activation Functions

Softplus is often compared with other activation functions like ReLU and sigmoid in terms of performance and suitability for different types of neural networks. Understanding when and where to use Softplus, as opposed to other functions, depends largely on the specific characteristics of the problem and the network architecture.

Conclusion

The Softplus activation function offers a continuously differentiable alternative to ReLU, suitable for various applications in neural networks. Its smoothness and non-zero gradient everywhere make it a robust choice in scenarios where the maintenance of active and healthy gradient flow is crucial for the training process.

References

1. Dugas, Charles, et al. "Incorporating Second-Order Functional Knowledge for Better Option Pricing." Advances in Neural Information Processing Systems, 2001.
2. Glorot, Xavier, and Yoshua Bengio. "Understanding the Difficulty of Training Deep Feedforward Neural Networks." Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010, pp. 249-256.