Softmax Activation

Introduction

The softmax activation function is a crucial component in the field of machine learning, particularly in the context of classification problems where it is used to handle multiple classes. The softmax function is typically applied in the output layer of a neural network model to transform logits—raw prediction values computed by the model—into probabilities that sum to one. This property makes softmax particularly useful for categorical classification.

Background and Theory

The softmax function is an extension of the logistic function to multiple dimensions. It is used in various types of neural networks, including deep learning models like Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), especially in scenarios where the outputs are mutually exclusive.

Mathematical Foundations

Mathematically, the softmax function can be defined as follows:

Given a vector $\mathbf{z}$ consisting of real values $z_1, z_2, \ldots, z_n$, the softmax function $\sigma(\mathbf{z})_i$ for each component $i$ of the output vector is computed as:

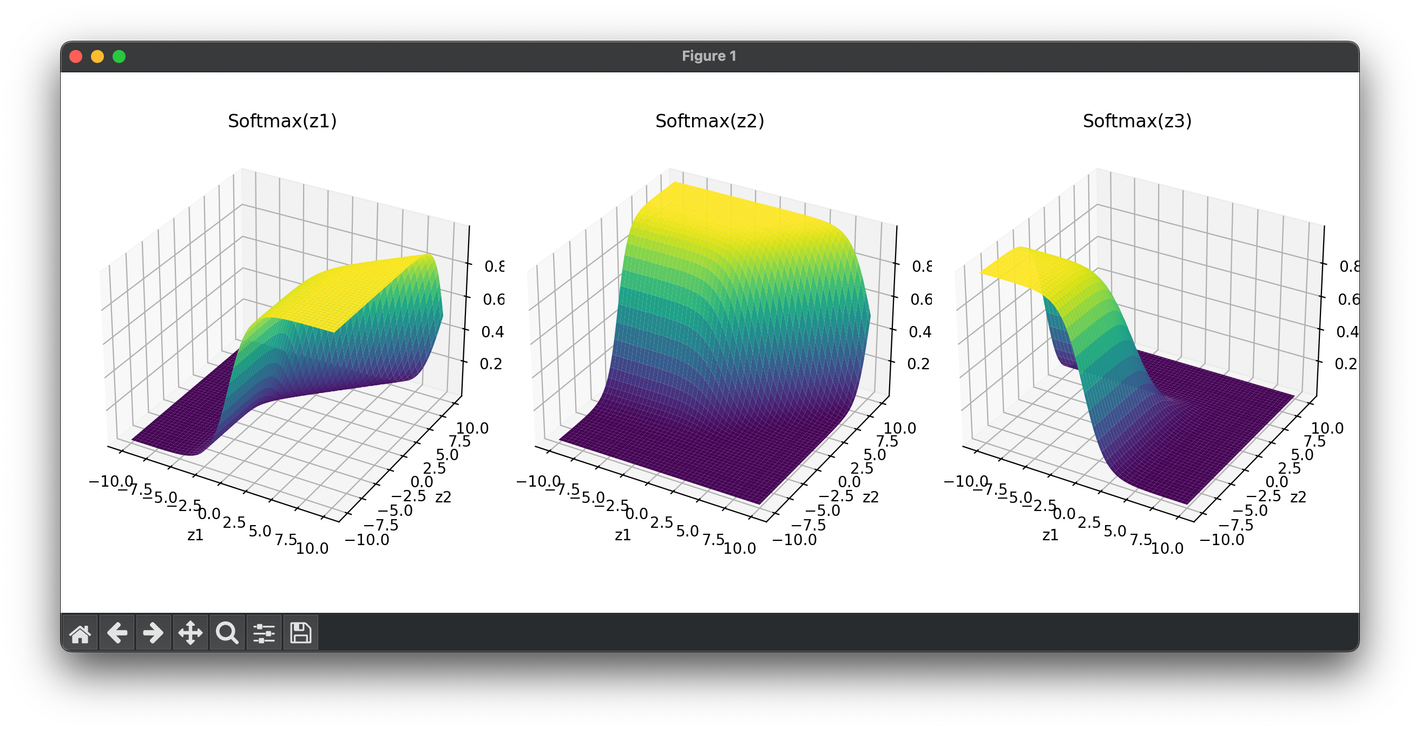
This formula ensures that each output is in the range $(0,1)$, and all outputs sum to 1.

Procedural Steps

1. Compute the Exponentials: For each component $z_i$ of the input vector $\mathbf{z}$, compute $e^{z_i}$.
2. Sum the Exponentials: Calculate the sum of all the exponential values computed from the input vector.
3. Divide by the Sum: For each component $z_i$, divide $e^{z_i}$ by the total sum of exponentials to get $\sigma(\mathbf{z})_i$.

Applications

Softmax is widely used in machine learning in scenarios such as:

• Multiclass Classification: Where each instance could belong to one of many classes.
• Language Modeling: In natural language processing (NLP), where the model predicts the probability distribution of the next word in the sequence.
• Reinforcement Learning: To choose actions based on probability distributions derived from the estimated rewards.

Strengths and Limitations

Strengths

• Probabilistic Interpretation: Outputs can be interpreted as probabilities, providing a clear and interpretable output from models.
• Differentiability: The function is differentiable, allowing it to be used in backpropagation in neural networks.

Limitations

• Exponential Computation: The computation of exponentials can be computationally expensive and prone to numerical instability (e.g., overflow/underflow issues).
• Non-Zero Probabilities: It assigns a non-zero probability to all classes, which may be impractical if some classes are highly unlikely given the input.

Advanced Topics

Numerical Stability

To improve numerical stability, a modified version of the softmax function is often used:

This adjustment involves subtracting the maximum value of $\mathbf{z}$ from each $z_i$ before computing the exponentials, thereby preventing overly large exponents and improving numerical stability.

Conclusion

The softmax activation function is integral to neural networks dealing with classification tasks. Its ability to convert logits to normalized probability scores makes it indispensable in many machine learning frameworks. Despite its computational challenges, softmax remains a fundamental component in neural networks, particularly in the output layers where probabilistic outputs are required.

References

1. Goodfellow, Ian, et al. "Deep Learning." MIT Press, 2016, pp. 179-196.
2. Bishop, Christopher M. "Pattern Recognition and Machine Learning." Springer, 2006, pp. 205-234.