Flatten Layer

Introduction

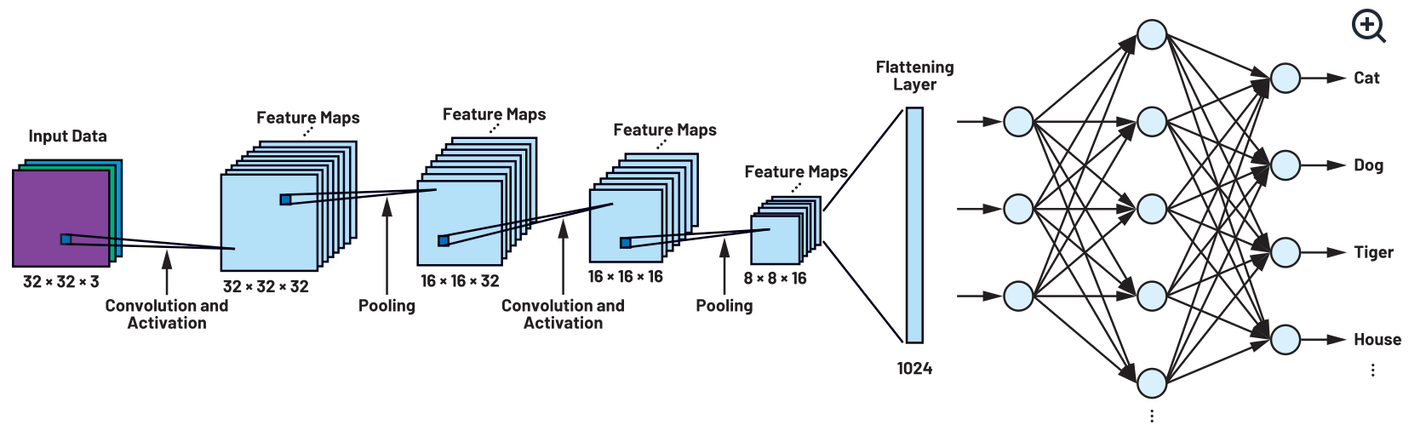
The Flatten layer is a crucial component in the architecture of many deep learning models, particularly those dealing with image and video processing, such as Convolutional Neural Networks (CNNs). Its primary function is to convert a multi-dimensional input tensor into a single-dimensional tensor (vector), facilitating the transition between convolutional layers and fully connected layers (dense layers) in a neural network.

Background and Theory

In convolutional neural networks, data processed through convolutional layers retains a multi-dimensional format (e.g., height, width, channels), which is not suitable for the fully connected layers that typically follow. These layers expect input data in a flat, one-dimensional format. The Flatten layer addresses this requirement by reshaping the tensor without altering the batch size or data content.

Mathematical Foundations

The operation of a Flatten layer can be understood as a tensor reshaping process. Given a tensor with dimensions $(N, C, H, W)$—where $N$ is the batch size, $C$ is the number of channels, $H$ is the height, and $W$ is the width—the Flatten layer transforms this tensor into a new shape $(N, C \cdot H \cdot W)$. This transformation maintains the integrity of the data but changes its organization to suit the requirements of subsequent layers.

Procedural Steps

1. Input Reception: The Flatten layer receives an input tensor, generally the output from preceding convolutional layers.
2. Tensor Reshaping: The layer reshapes the input tensor from a multi-dimensional format to a single-dimensional format per instance in the batch. This is done while preserving the batch size as the leading dimension.
3. Output Delivery: The reshaped tensor is then passed to the next layer in the network, typically a fully connected layer.

Mathematical Formulation

The reshaping operation performed by a Flatten layer can be represented mathematically as follows:

Given an input tensor $X$ of dimensions $(N, C, H, W)$, the Flatten layer outputs a tensor $Y$ of dimensions $(N, K)$ where $K = C \times H \times W$. The elements of $Y$ are filled as:

where

This formula calculates the linear index $k$ of the flattened output by mapping the multi-dimensional indices $c$, $h$, and $w$ of the input tensor $X$.

Implementation

Parameters

No parameters.

Applications

• Data Preparation for Dense Layers: By transforming multi-dimensional data from convolutional layers into a format suitable for dense layers, the Flatten layer facilitates a seamless transition in neural network architectures.
• Feature Consolidation: In tasks such as image classification, flattening the convolutional outputs consolidates features into a format amenable to classification layers.

Strengths and Limitations

Strengths

• Simplicity and Efficiency: The Flatten layer is simple to implement and involves minimal computational overhead, as it primarily rearranges data without performing any complex operations.
• Versatility: It is essential in CNNs but also finds use in other model architectures where dimensionality reduction is necessary.

Limitations

• Loss of Spatial Information: Flattening the data can lead to a loss of spatial relationships, which might be detrimental for some tasks where spatial context is crucial.
• Scalability Issues: With large input sizes, the output dimension after flattening can become very large, potentially leading to issues with model size and overfitting.

Advanced Topics

• Memory Optimization: In practice, some deep learning frameworks optimize the Flatten operation to be memory-efficient, avoiding the need to physically rearrange data in memory.
• Alternative Approaches: Techniques such as Global Average Pooling are sometimes used as alternatives to flattening, particularly to preserve some spatial features while still reducing dimensionality.

References

1. Goodfellow, Ian, et al. "Deep Learning." MIT Press, 2016.
2. LeCun, Yann, et al. "Gradient-based learning applied to document recognition." Proceedings of the IEEE, 1998.