Swish

Introduction

The Swish activation function is a relatively recent addition to the repertoire of activation functions used in deep learning. Introduced by researchers at Google, Swish is a smooth, non-monotonic function that has shown promising results in terms of improving the performance of deep neural networks compared to traditional functions like ReLU. Its formulation includes a self-gating mechanism, which allows the function to modulate the input based on the input itself.

Background and Theory

Swish is part of a family of activation functions that are continuously differentiable and non-monotonic. The idea behind Swish is to combine aspects of both ReLU and sigmoid functions to provide better performance, particularly in deeper networks where vanishing or exploding gradients can impede learning.

Mathematical Foundations

The Swish function is defined by the following formula:

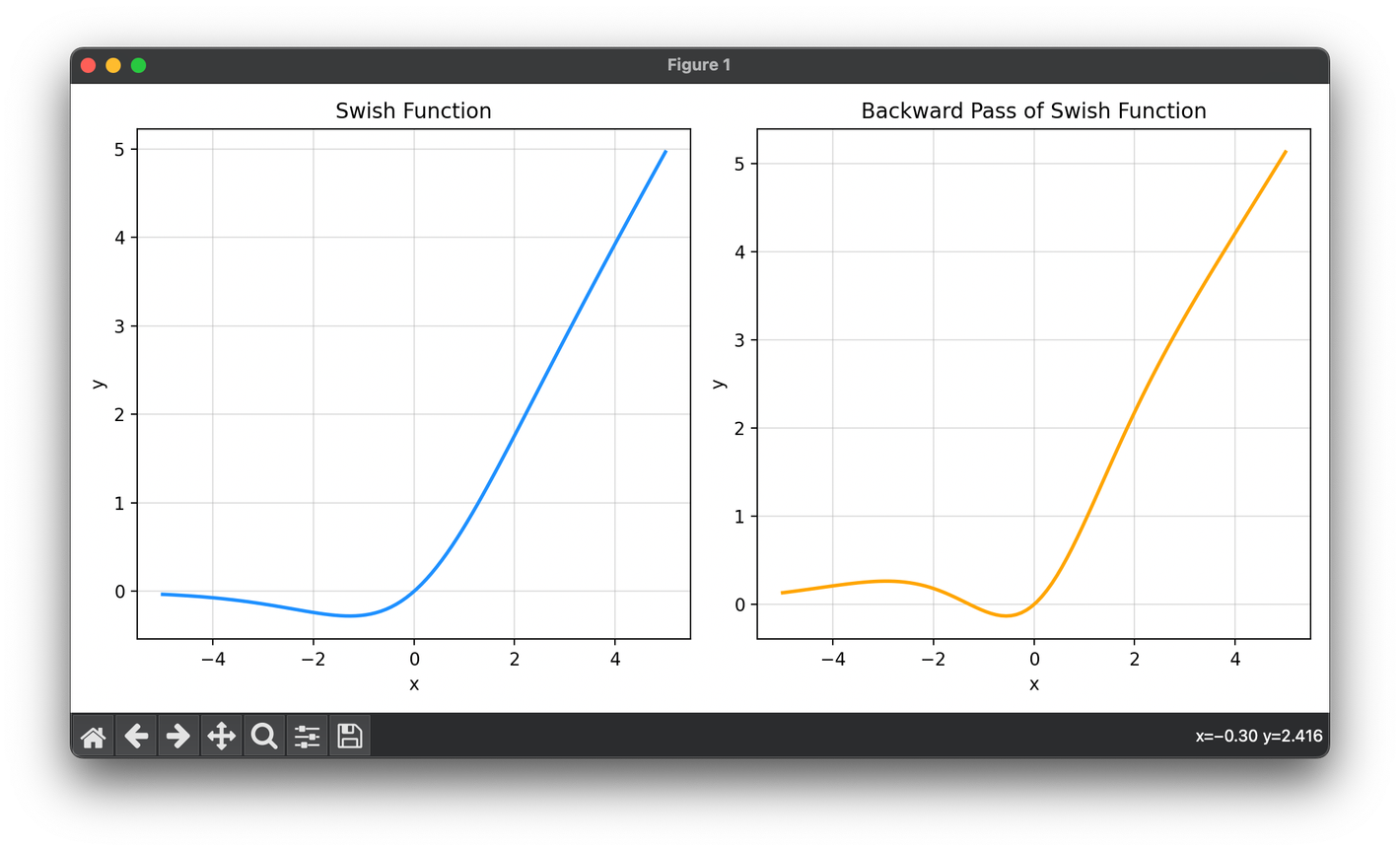
where $\sigma(x)$ is the sigmoid function, $\sigma(x) = \frac{1}{1 + e^{-x}}$, and $\beta$ is either a constant or a trainable parameter. When $\beta = 1$, Swish simplifies to $x \cdot \sigma(x)$.

Procedural Steps

1. Computation of Sigmoid: Compute the sigmoid function of $\beta x$, where $\beta$ can be a constant or a trainable parameter of the model.

2. Multiplication: Multiply the input $x$ by the result of the sigmoid computation to obtain the output of the Swish function.

3. Backpropagation: Compute the gradient for backpropagation, which for Swish involves both the function itself and its derivative:

   $\frac{d}{dx}\text{Swish}(x) = \text{Swish}(x) + \sigma(\beta x)(1 - \text{Swish}(x))$

Applications

Swish has been effectively used in various types of neural networks, including:

• Convolutional Neural Networks (CNNs): Where it has sometimes outperformed ReLU in image recognition tasks.
• Deep Feedforward Networks: Its smoothness and gradient properties can enhance training in deep architectures.
• Recurrent Neural Networks (RNNs): Swish's properties may help in mitigating issues like vanishing gradients.

Strengths and Limitations

Strengths

• Smoothness: Being continuously differentiable everywhere, Swish avoids issues related to non-differentiability.
• Adaptiveness: The inclusion of the parameter $\beta$ allows the function to adapt its shape based on the data or during training if $\beta$ is trainable.
• Improved Performance: Research has shown that Swish can outperform ReLU in various tasks, potentially due to its dynamic gating mechanism.

Limitations

• Computational Complexity: Compared to ReLU, Swish is computationally more intensive due to the involvement of the exponential function in the sigmoid calculation.
• Parameter Tuning: If $\beta$ is trainable, it introduces additional complexity and parameters into the network, which might increase the training time and the risk of overfitting.

Advanced Topics

Learnable Parameters

The aspect of Swish that allows $\beta$ to be a trainable parameter can be explored further to understand how it impacts the learning dynamics of different neural networks. This feature introduces an additional level of adaptability, potentially enabling the activation function to optimize itself for specific tasks during training.

Conclusion

The Swish activation function is a versatile and powerful tool in neural network design, offering a combination of smoothness, adaptability, and potential performance gains over traditional activation functions like ReLU. Its introduction reflects ongoing innovations in neural network research, aiming to optimize network performance across a wide range of tasks.

References

1. Ramachandran, Prajit, et al. "Searching for Activation Functions." arXiv preprint arXiv:1710.05941, 2017.
2. Elfwing, Stefan, Eiji Uchibe, and Kenji Doya. "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning." Neural Networks, 2018, pp. 105-115.