Cross-Entropy Loss

Introduction

Cross-entropy loss, also known as log loss, measures the performance of a classification model whose output is a probability value between 0 and 1. Cross-entropy loss increases as the predicted probability diverges from the actual label. It is commonly used in models where the target variable is categorical, typically in binary or multiclass classification tasks. The purpose of cross-entropy loss is to quantify the difference between two probability distributions - the predicted probabilities and the actual distribution.

Background and Theory

Mathematical Foundations

The concept of cross-entropy is rooted in information theory, originally introduced by Claude Shannon. It is a measure of the difference between two probability distributions for a given random variable or set of events. In the context of machine learning, cross-entropy is a way to measure the dissimilarity between the distribution of the predicted probabilities by the model and the distribution of the actual labels.

The cross-entropy loss for two discrete probability distributions, $p$ and $q$, over a given set is defined as follows:

Where:

• $p(x)$ is the true probability of an outcome $x$,
• $q(x)$ is the predicted probability of an outcome $x$.

Binary Cross-Entropy Loss

In binary classification, where the labels are either 0 or 1, the formula for binary cross-entropy loss is:

Here:

• $y_i$ represents the actual label of the $i^{th}$ instance,
• $\hat{y}_i$ is the predicted probability of the $i^{th}$ instance being of class 1,
• $N$ is the total number of instances.

Multiclass Cross-Entropy Loss

For multiclass classification, the cross-entropy loss is extended to multiple classes:

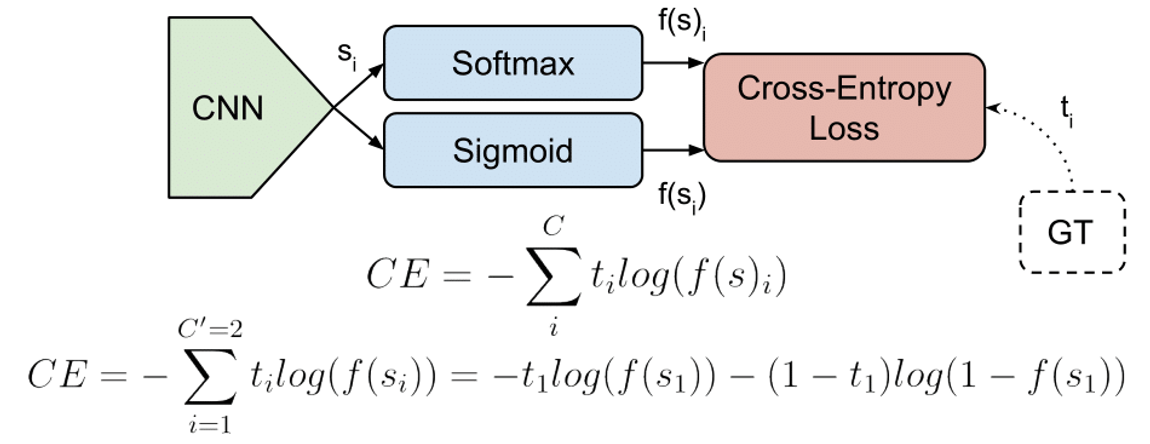
Where:

• $C$ is the number of classes,
• $y_{ic}$ is a binary indicator (0 or 1) if class label $c$ is the correct classification for observation $i$,
• $\hat{y}_{ic}$ predicts probability observation $i$ is of class $c$.

Procedural Steps

To implement cross-entropy loss in a machine learning model, follow these general steps:

1. Model Output: Ensure the model outputs probabilities, typically using a softmax function for multiclass classification or a sigmoid function for binary classification.
2. Calculate Loss: Use the formulas provided to calculate the cross-entropy loss for each instance in the dataset.
3. Compute Gradient: Derive the gradient of the loss function with respect to each weight in the model, which is necessary for model optimization during training.
4. Optimize: Use an optimization algorithm, such as gradient descent, to minimize the loss by adjusting the weights.

Applications

Cross-entropy loss is extensively used in:

• Binary classification tasks, like email spam detection.
• Multiclass classification tasks, such as image classification and natural language processing applications.

Strengths and Limitations

Strengths:

• Highly effective for classification problems where outputs are probabilities.
• Directly penalizes the probability based on the distance from the actual label.

Limitations:

• Sensitive to imbalanced datasets which might skew the distribution of the errors.
• Can lead to numerical instability due to the logarithmic component; this is typically mitigated by adding a small constant to the logarithm argument.

Advanced Topics

Relationship with KL Divergence

Kullback-Leibler divergence is a measure of how one probability distribution diverges from a second, expected probability distribution. Cross-entropy can be decomposed into the entropy of the true distribution plus the KL divergence between the true and the predicted distributions:

Understanding this relationship can help in better grasping the effectiveness of cross-entropy in terms of measuring probabilistic discrepancies.

References

1. "Pattern Recognition and Machine Learning" by Christopher M. Bishop.
2. "Deep Learning" by Ian Goodfellow, Yoshua Bengio, and Aaron Courville.
3. Shannon, Claude E. "A Mathematical Theory of Communication." Bell System Technical Journal 27 (1948): 379–423, 623–656.