[Classifier] Decision Tree Classifier

안암동컴맹·2024년 2월 25일

Machine Learning

목록 보기

14/103

Decision Tree Classifier

Introduction

A Decision Tree Classifier is a non-parametric supervised learning method used for classification and regression tasks. It models decisions and their possible consequences as a tree structure, incorporating chance event outcomes, resource costs, and utility. Decision Trees are easy to interpret, handle categorical and numerical data, and can visually represent decision-making processes, making them a popular choice across various domains.

Background and Theory

The core idea behind Decision Trees is to mimic human decision-making processes by splitting data into subsets based on feature values. This process is repeated recursively, resulting in a tree-like model of decisions. The decisions or splits are made at nodes based on the outcome that provides the best separation of the data according to a specific criterion, such as Gini impurity or information gain.

Types of Decision Trees

Classification Trees: Used when the target variable is categorical. The aim is to predict a discrete class label for each node.
Regression Trees: Used when the target variable is continuous. The goal is to predict a continuous quantity.

How the Algorithm Works

Construction

Start at the Root: Begin with the entire dataset as the root node.
Feature Selection: At each node, select the feature that best splits the data according to a certain criterion (e.g., Gini impurity, information gain).
Branching: Create branches for each possible value of the selected feature, splitting the dataset accordingly.
Recursive Splitting: Repeat the process for each branch, using the subset of data for that branch, until one of the stopping criteria is met.
Termination: The recursion is halted when a node has all samples of the same class (pure node), a maximum depth is reached, or another predetermined stopping criterion is met.
Prediction: For classification, the prediction is the most frequent class in the leaf nodes. For regression, it's the average target value.

Splitting Criteria

Gini Impurity: A measure of how often a randomly chosen element would be incorrectly identified. It aims to minimize the probability of misclassification.
Entropy/Information Gain: Entropy is a measure of the randomness in the information being processed. The higher the entropy, the harder it is to draw any conclusions from that information. Information gain is based on the decrease in entropy after a dataset is split on an attribute. Constructing a decision tree is all about finding an attribute that returns the highest information gain and the smallest entropy.

Mathematical Formulation

When constructing a Decision Tree Classifier, the mathematical formulations governing the selection of splits are crucial for understanding its decision-making process. Let's delve deeper into these formulations, particularly focusing on Gini impurity, Entropy, and Information Gain, as these are central to how decision trees decide where to split the data.

Gini Impurity

Gini Impurity measures the frequency at which any element from the set will be mislabeled when it is randomly labeled according to the distribution of labels in the subset. The Gini Impurity for a dataset is:

G(S) = 1 - \sum_{i=1}^{n} p_i^2

$G(S)$ : Gini impurity of the set $S$ .
$p_i$ : Proportion of elements belonging to class $i$ in the subset.

For a binary classification problem, this simplifies to $G(S) = 1 - (p^2 + (1-p)^2)$ , where $p$ is the proportion of elements of one class. The goal is to minimize Gini impurity at each split, which corresponds to increasing the purity of the subsets formed by the split.

Entropy

Entropy measures the amount of information disorder or uncertainty. In the context of a decision tree, it quantifies the impurity or randomness in the class labels of the dataset. The entropy of a set $S$ is defined as:

H(S) = -\sum_{i=1}^{n} p_i \log_2(p_i)

$H(S)$ : Entropy of the set $S$ .
$p_i$ : Proportion of elements belonging to class $i$ in the subset.s

Entropy reaches its maximum value when all classes in the set are equally represented, indicating the highest uncertainty. A set with only one class (pure) has an entropy of 0.

Information Gain

Information Gain is the reduction in entropy or impurity achieved by partitioning the data according to a particular attribute. It is a measure of how well a given attribute separates the training examples according to their target classification. Information Gain for a split on attribute $A$ is calculated as:

IG(S, A) = H(S) - \sum_{j} \frac{|S_j|}{|S|} H(S_j)

$IG(S, A)$ : Information Gain of the set $S$ after splitting on attribute $A$ .
$H(S)$ : Initial entropy of the set before the split.
$S_j$ : Subset of $S$ for a particular value of $A$ .
$|S_j|/|S|$ : Weight of the $j$ -th subset, representing the proportion of the number of elements in subset $S_j$ to the number of elements in the entire set $S$ .

The attribute that maximizes the Information Gain is chosen for the split at each node of the tree. This process aims to increase the homogeneity of the subsets, which ideally would have entropy values moving closer to 0 (increasing purity).

Considerations in Split Selection

Trade-offs: While higher Information Gain or lower Gini impurity are desirable, they are not the only factors to consider. The complexity of the tree, potential for overfitting, and computational efficiency also play crucial roles in deciding the practicality of a split.
Stopping Criteria: Besides the mathematical formulations, decision trees also rely on stopping criteria to prevent overfitting. These criteria include setting a maximum depth for the tree, requiring a minimum number of samples to split a node, and setting a minimum gain in reduction of impurity.

Decision Tree Splitting Algorithms

Decision Trees use different algorithms to decide on the best split. The most common are ID3 (Iterative Dichotomiser 3), C4.5 (a successor of ID3), and CART (Classification and Regression Trees). Each algorithm has its methodology for selecting the best split:

ID3 and C4.5 focus on maximizing Information Gain and the Gain Ratio (an extension used in C4.5 to address Information Gain's bias towards attributes with a large number of values).
CART uses Gini Impurity as its criterion for making splits.

Mathematical Consideration for Best Split

The process of determining the best split involves calculating the chosen metric (e.g., Gini Impurity, Entropy) for every possible split and then selecting the one that results in the highest gain (for Information Gain) or the lowest impurity (for Gini Impurity).

Calculating Gain for a Potential Split

Suppose we're considering a split on a particular feature. We calculate the metric for each subset that would result from the split and then combine these to get a weighted sum or average that represents the entire dataset after the split. The improvement (or gain) from a split is the difference between the metric before the split and this weighted sum after the split.

For Information Gain, specifically, you calculate the gain for a potential split on attribute $A$ as follows:

IG(S, A) = H(S) - \sum_{v \in \mathcal{V}(A)} \frac{|S_v|}{|S|} H(S_v)

$\mathcal{V}(A)$ : The set of all possible values for attribute $A$ .
$S_v$ : The subset of $S$ for which attribute $A$ has value $v$ .

For Gini Impurity, the improvement from a potential split can be measured as a decrease in impurity:

\Delta Gini(S, A) = G(S) - \sum_{v \in \mathcal{V}(A)} \frac{|S_v|}{|S|} G(S_v)

The split that provides the highest Information Gain or the largest decrease in Gini Impurity is selected as the best split.

Practical Example

Let's consider a practical example with a dataset containing two features $F_1$ and $F_2$ , and we want to determine the best feature to split on at the current node:

Calculate the current impurity of the node (using either Gini Impurity or Entropy, depending on the algorithm).
For each feature:
- For every possible value (or range of values) that the feature can take, split the dataset into two subsets.
- Calculate the impurity for each subset.
- Compute the weighted average of these impurities.
- Determine the improvement (gain) this split would bring about.
Compare the gains across all possible splits and select the feature and value that offer the highest gain (or largest decrease in impurity).

Considerations in Splitting

Overfitting: A tree that is too deep can overfit the data, capturing noise rather than the underlying pattern. Techniques like pruning (removing parts of the tree that don't provide additional power) are used to combat this.
Minimum Gain Threshold: Some implementations allow setting a minimum gain threshold for a split to be considered. This prevents making splits that do not significantly improve the model's predictions.
Cost-Complexity Pruning: Beyond just looking at impurity reduction, considering the trade-off between the tree's complexity and its accuracy is crucial. CART, for example, uses cost-complexity pruning to find the optimal trade-off by penalizing the number of leaves.

In summary, the mathematical formulation and consideration for the best split in a Decision Tree involve analyzing the potential decrease in impurity or increase in information gain across all possible splits. The choice of metric and the method for calculating this improvement are fundamental to the tree's ability to learn from the training data effectively and generalize well to unseen data.

Implementation

Parameters

max_depth: int, default = 10
Maximum depth of the tree
criterion: Literal['gini', 'entropy'], default = ‘gini’
Function used to measure the quality of a split
min_samples_split: int, default = 2
Minimum samples required to split a node
min_samples_leaf: int, default = 1
Minimum samples required to be at a leaf node
max_features: int, default = None
Number of features to consider
min_impurity_decrease: float, default = 0.01
Minimum decrement of impurity for a split
max_leaf_nodes: int, default = None
Maximum amount of leaf nodes
random_state: int, default = None
The randomness seed of the estimator

Examples

Test on synthesized $\mathbb{R}^{n\times5}$ dataset with PCA and RandomizedSearchCV:

from luma.classifier.tree import DecisionTreeClassifier
from luma.preprocessing.scaler import StandardScaler
from luma.reduction.linear import PCA
from luma.model_selection.split import TrainTestSplit
from luma.model_selection.search import RandomizedSearchCV
from luma.visual.evaluation import DecisionRegion, ConfusionMatrix

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np


X, y = make_classification(n_samples=400,
                           n_classes=4,
                           n_features=5,
                           n_informative=4,
                           n_redundant=1,
                           n_clusters_per_class=1,
                           class_sep=2.0,
                           random_state=0)

X_train, X_test, y_train, y_test = TrainTestSplit(X, y,
                                                  test_size=0.2,
                                                  random_state=42).get

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.fit_transform(X_test_std)

param_dist = {'max_depth': [5, 10, 20, 50],
              'criterion': ['gini', 'entropy'],
              'min_impurity_decrease': np.linspace(0, 0.2, 10)}

rand = RandomizedSearchCV(estimator=DecisionTreeClassifier(),
                          param_dist=param_dist,
                          max_iter=50,
                          cv=5,
                          refit=True,
                          random_state=42,
                          verbose=True)

rand.fit(X_train_pca, y_train)
tree_best = rand.best_model

X_concat = np.concatenate((X_train_pca, X_test_pca))
y_concat = np.concatenate((y_train, y_test))

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec = DecisionRegion(tree_best, X_concat, y_concat, cmap='plasma')
dec.plot(ax=ax1)

conf = ConfusionMatrix(y_concat, tree_best.predict(X_concat))
conf.plot(ax=ax2, show=True)

# Best params: {
#     'max_depth': 5, 
#     'criterion': 'entropy', 
#     'min_impurity_decrease': 0.2
# }
# Best score: 0.940625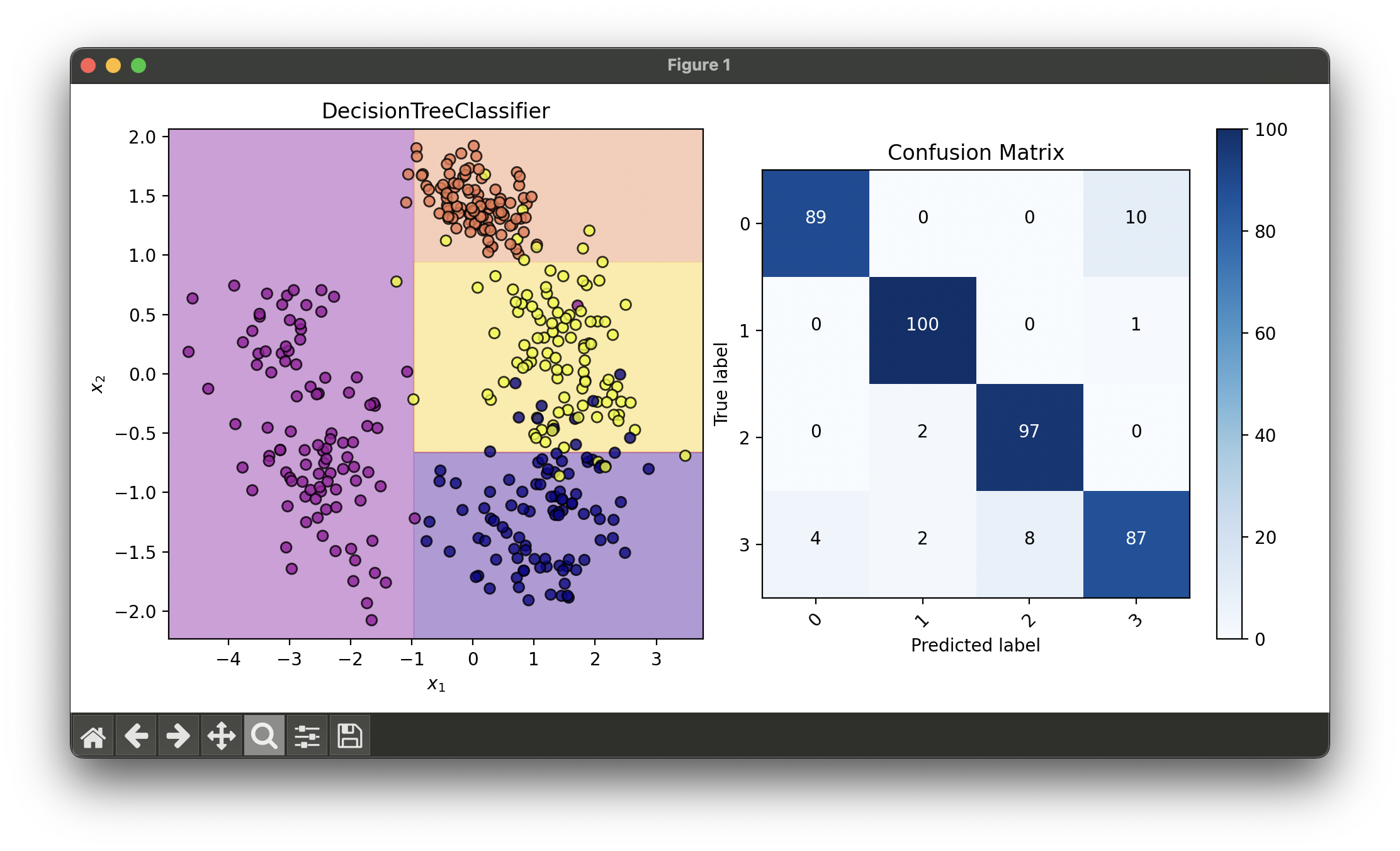

Applications and Use Cases

Medical Diagnosis: Predicting the presence of diseases based on symptoms and test results.
Financial Analysis: Assessing loan applicants' creditworthiness based on their financial history.
Customer Segmentation: Grouping customers based on purchasing behavior for targeted marketing.
Fault Diagnosis: Identifying failure modes in manufacturing and maintenance processes.

Strengths and Limitations

Strengths
- Interpretability: Trees can be visualized, making the model easy to interpret.
- Handling of Non-linear Relationships: Capable of capturing non-linear relationships without the need for data transformation.
- Feature Importance: Provides insights into the most significant variables in prediction.
Limitations
- Overfitting: Without proper tuning, trees can become complex and overfit the training data.
- Variance: Small changes in the data can result in a completely different tree being generated.
- Bias: Decision trees can be biased towards splits on features with more levels.

Advanced Topics and Further Reading

Pruning: Techniques to reduce the size of a decision tree by removing sections of the tree that provide little power to classify instances.
Ensemble Methods: Combining multiple decision trees to improve performance, such as Random Forests and Gradient Boosted Trees.
Handling Missing Values: Strategies for dealing with missing data when building and using decision trees.
Alternative Splitting Criteria: Exploring other methods for selecting the best split, beyond Gini impurity and entropy.

References

Breiman, L., Friedman, J., Olshen, R.A., & Stone, C.J. (1984). Classification and Regression Trees. Wadsworth.

Quinlan, J.R. (1986). "Induction of Decision Trees". Machine Learning, 1(1), 81-106.

Rokach, L. & Maimon, O. (2005). Decision Trees for Machine Learning. Data Mining and Knowledge Discovery Handbook, Springer.

James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning. Springer Texts in Statistics.

안암동컴맹

𝖪𝗈𝗋𝖾𝖺 𝖴𝗇𝗂𝗏. 𝖢𝗈𝗆𝗉𝗎𝗍𝖾𝗋 𝖲𝖼𝗂𝖾𝗇𝖼𝖾 & 𝖤𝗇𝗀𝗂𝗇𝖾𝖾𝗋𝗂𝗇𝗀