AdaBoost Classifier

Introduction

AdaBoost, short for Adaptive Boosting, is an ensemble learning method that is used primarily for classification tasks. It combines multiple weak classifiers to create a strong classifier. By focusing on examples that are hard to predict, AdaBoost is able to improve the performance of the model iteratively. The algorithm assigns weights to each training example and adjusts these weights after each classifier is trained, thereby giving higher weight to the examples that were misclassified by the previous classifiers.

Background and Theory

AdaBoost belongs to the family of boosting algorithms. The central idea behind boosting is to take a set of weak classifiers (models that perform slightly better than random guessing) and to combine them into a single strong classifier. AdaBoost does this by building a model from the training data, then creating a second model that attempts to correct the errors from the first model. This process is repeated, adding models until either the training data is predicted perfectly or the maximum number of estimators is added.

Mathematical Foundations

Given a dataset $D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$ where $x_i$ represents the features of each instance, and $y_i \in \{-1, 1\}$ represents the class labels, the AdaBoost algorithm iteratively selects a weak classifier $h_t(x)$ at each round $t$ that minimizes the weighted classification error:

where $w_i$ is the weight of the $i^{th}$ instance, and $I(\text{condition})$ is an indicator function that returns 1 if the condition is true, and 0 otherwise.

The weights of incorrectly classified instances are increased, and the weights of correctly classified instances are decreased. The weight update rule is:

where $\alpha_t = \frac{1}{2} \ln(\frac{1 - \epsilon_t}{\epsilon_t})$ is the weight of the classifier $h_t(x)$ in the final model.

The final model is a linear combination of the weak classifiers:

where $T$ is the total number of weak classifiers.

Procedural Steps

1. Initialize Weights: Initially, all training examples are given the same weight, $w_i = 1/n$ for all $i$, where $n$ is the number of training examples.
2. For $t = 1$ to $T$ (or until termination condition is met):
   • Train a weak classifier $h_t(x)$ using the weighted training data.
   • Calculate the error $\epsilon_t$ of $h_t(x)$ on the training data.
   • Compute $\alpha_t$, the weight of $h_t(x)$, based on $\epsilon_t$.
   • Update the weights $w_i$ for each training example.
   • Normalize the weights so that they sum up to 1.
3. Output the final model: The final model is a weighted vote of the weak classifiers: $H(x) = \text{sign} \left( \sum_{t=1}^{T} \alpha_t h_t(x) \right)$

Implementation

Parameters

• base_estimator: Estimator, default = DecisionTreeClassifier()
  Base estimator for training multiple models
  
• n_estimators: int, default = 100
  Number of base estimators to fit
  
• learning_rate: float, default = 1.0
  Step size of class weights($\vec\alpha$) update
  

Examples

Test on standardized and reduced($\mathbb{R}^{n\times64}\rightarrow\mathbb{R}^{n\times2}$) digits dataset with only 4 classes:

from luma.ensemble.boost import AdaBoostClassifier
from luma.preprocessing.scaler import StandardScaler
from luma.model_selection.split import TrainTestSplit
from luma.reduction.linear import KernelPCA
from luma.visual.evaluation import DecisionRegion, ConfusionMatrix

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(42)

X, y = load_digits(n_class=4, return_X_y=True)
indices = np.random.choice(X.shape[0], size=500)

X_sample = X[indices]
y_sample = y[indices]

sc = StandardScaler()
X_sample_std = sc.fit_transform(X_sample)

kpca = KernelPCA(n_components=2, gamma=0.01, kernel='rbf')
X_kpca = kpca.fit_transform(X_sample_std)

X_train, X_test, y_train, y_test = TrainTestSplit(X_kpca, y_sample, 
                                                  test_size=0.3).get

ada = AdaBoostClassifier(n_estimators=100, learning_rate=1.0)
ada.fit(X_train, y_train)

X_cat = np.concatenate((X_train, X_test))
y_cat = np.concatenate((y_train, y_test))

score = ada.score(X_cat, y_cat)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec = DecisionRegion(ada, X_cat, y_cat, 
                     title=f'AdaBoostClassifier [Acc: {score:.4f}]', 
                     cmap='viridis')
dec.plot(ax=ax1)

conf = ConfusionMatrix(y_cat, ada.predict(X_cat))
conf.plot(ax=ax2, show=True)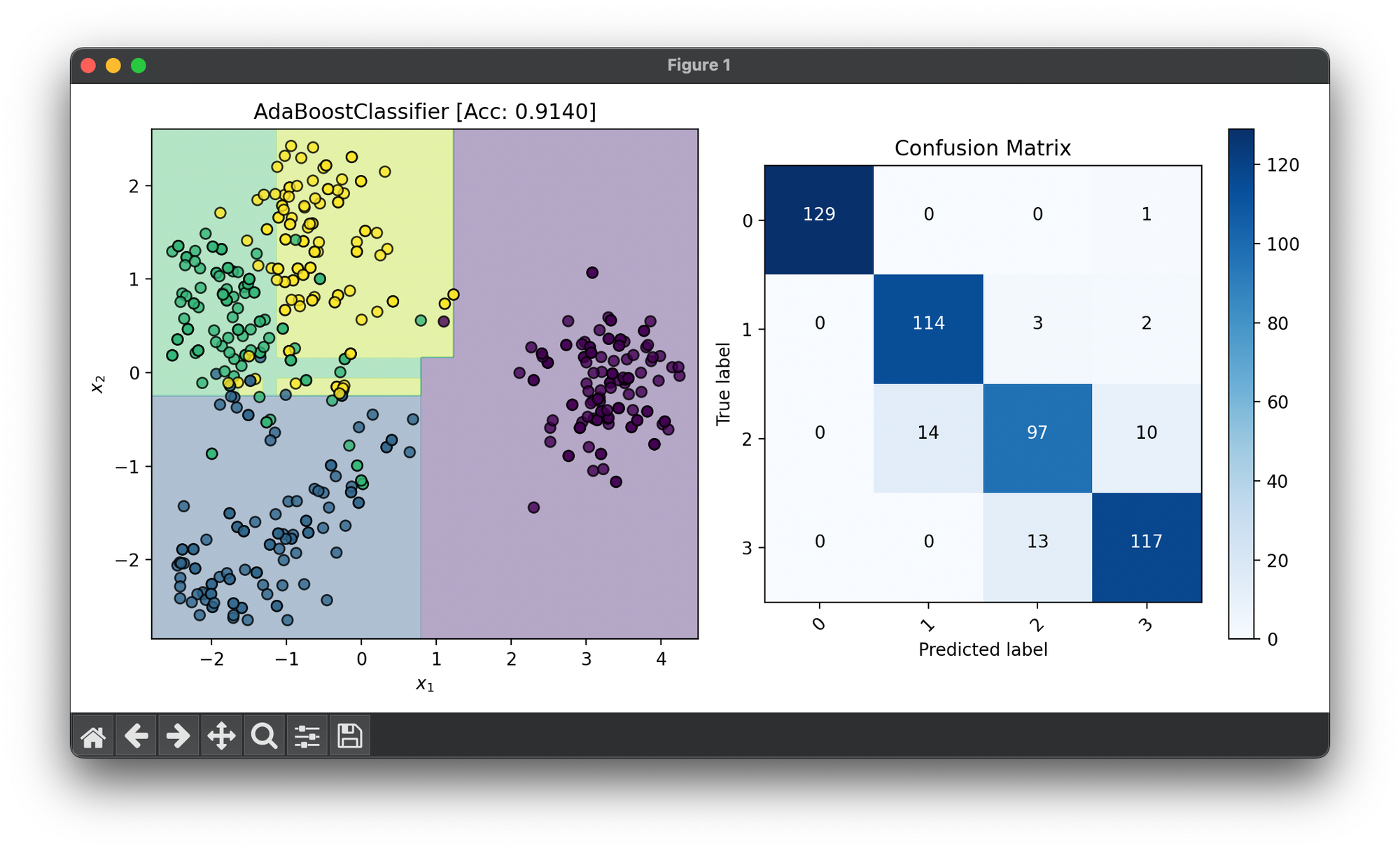

Applications

• Binary Classification: AdaBoost is widely used for binary classification tasks, such as spam detection or binary decision problems.
• Multi-Class Classification: With a technique called "Samme" or by converting into multiple binary classification tasks, AdaBoost can also be applied to multi-class classification problems.
• Feature Selection: The iterative process of AdaBoost can highlight features that are more informative for classification, thus it can be used for feature selection purposes.

Strengths and Limitations

Strengths

• Simple to Implement: AdaBoost is straightforward to implement and has few parameters to adjust.
• Versatile: It can be used with any learning algorithm and for a wide range of classification problems.
• Automatically Handles Overfitting: In some cases, AdaBoost can be less prone to overfitting, especially when the data is noise-free and the base classifiers are weak.

Limitations

• Sensitive to Noisy Data: AdaBoost can be sensitive to noisy data and outliers since it tries to fit each point perfectly.
• Computationally Intensive: The sequential nature of boosting can make the training process longer and computationally more intensive than other algorithms.

Advanced Topics

• AdaBoost.M1, AdaBoost.R2, AdaBoost.RT: Variants of AdaBoost for handling multi-class classification problems and regression.
• Feature Importance in AdaBoost: Understanding how AdaBoost assigns importance to features and how this can be used for feature selection.

References

1. Freund, Yoav, and Robert E. Schapire. "A decision-theoretic generalization of on-line learning and an application to boosting." Journal of computer and system sciences 55.1 (1997): 119-139.
2. Schapire, Robert E., and Yoav Freund. "Boosting: Foundations and algorithms." Kybernetika 47.6 (2011): 955-973.