Bagging Classifier

Introduction

The Bagging Classifier, short for Bootstrap Aggregating Classifier, is a machine learning ensemble meta-algorithm designed to improve the stability and accuracy of machine learning algorithms used in statistical classification and regression. It reduces variance and helps to avoid overfitting. Although it is usually applied to decision tree methods, it can be used with any type of method. Bagging is a special case of the model averaging approach.

Background and Theory

Bagging involves generating multiple versions of a predictor and using these to get an aggregated predictor. The method involves three main steps: bootstrapping the dataset, applying the algorithm to each bootstrapped dataset, and then aggregating the predictions. This approach leverages the power of multiple models to achieve a better performance than any of the individual models could.

Mathematical Foundations

Let's consider a training dataset $D$ of size $N$. Bagging generates $m$ new training sets $D_i$, each of size $N'$, by sampling from $D$ uniformly and with replacement. By sampling with replacement, some observations may be repeated in each $D_i$. The $m$ models are fitted using the above $m$ sets and combined by averaging the output (for regression) or voting (for classification).

Formally, if we have a set of predictions $\{y_1, y_2, \ldots, y_m\}$ from $m$ models, the aggregated prediction $\bar{y}$ for regression would be:

For classification problems, the aggregated prediction is the mode of the predictions:

Procedural Steps

1. Bootstrap the dataset: Create multiple bootstrapped datasets from the original dataset.
2. Apply the learning algorithm: Train a model on each of these datasets.
3. Combine predictions:
   • For regression tasks, average the predictions from all models.
   • For classification tasks, use majority voting from all models.

Implementation

Parameters

• base_estimator: Estimator, default = DecisionTreeClassifier()
  Base estimator for training multiple models
  
• n_estimators: int, default = 50
  Number of base estimators to fit
  
• max_samples: float int, default = 1.0
  Maximum number of data to sample (0~1 proportion)
  
• max_features: float int, default = 1.0
  Maximum number of features to sample (0~1 proporton)
  
• bootstrap: bool, default = True
  Whether to bootstrap data samples
  
• bootstrap_feature: bool, default = False
  Whether to bootstrap features
  

Examples

Test on reduced wine dataset with DecisionTreeClassifier() as a base estimator:

from luma.preprocessing.scaler import StandardScaler
from luma.reduction.linear import PCA
from luma.model_selection.split import TrainTestSplit
from luma.model_selection.search import RandomizedSearchCV
from luma.ensemble.bagging import BaggingClassifier
from luma.visual.evaluation import DecisionRegion, ConfusionMatrix

from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
import numpy as np

X, y = load_wine(return_X_y=True)

X_train, X_test, y_train, y_test = TrainTestSplit(X, y,
                                                  test_size=0.2,
                                                  random_state=42).get

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)

param_dist = {'n_estimators': [5, 10, 20, 50, 100],
              'max_samples': np.linspace(0.5, 1.0, 5),
              'bootstrap': [True, False],
              'bootstrap_feature': [True, False],
              'random_state': [42]}

rand = RandomizedSearchCV(estimator=BaggingClassifier(),
                          param_dist=param_dist,
                          max_iter=20,
                          cv=5,
                          refit=True,
                          random_state=42,
                          verbose=True)

rand.fit(X_train_pca, y_train)
bag_best = rand.best_model

X_cat = np.concatenate((X_train_pca, X_test_pca))
y_cat = np.concatenate((y_train, y_test))

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec = DecisionRegion(bag_best, X_cat, y_cat)
dec.plot(ax=ax1)

conf = ConfusionMatrix(y_cat, bag_best.predict(X_cat))
conf.plot(ax=ax2, show=True)

# Best params: {
#     'n_estimators': 100, 
#     'max_samples': 0.625, 
#     'bootstrap': True, 
#     'bootstrap_feature': True, 
# }
# Best score: 0.9571428571428573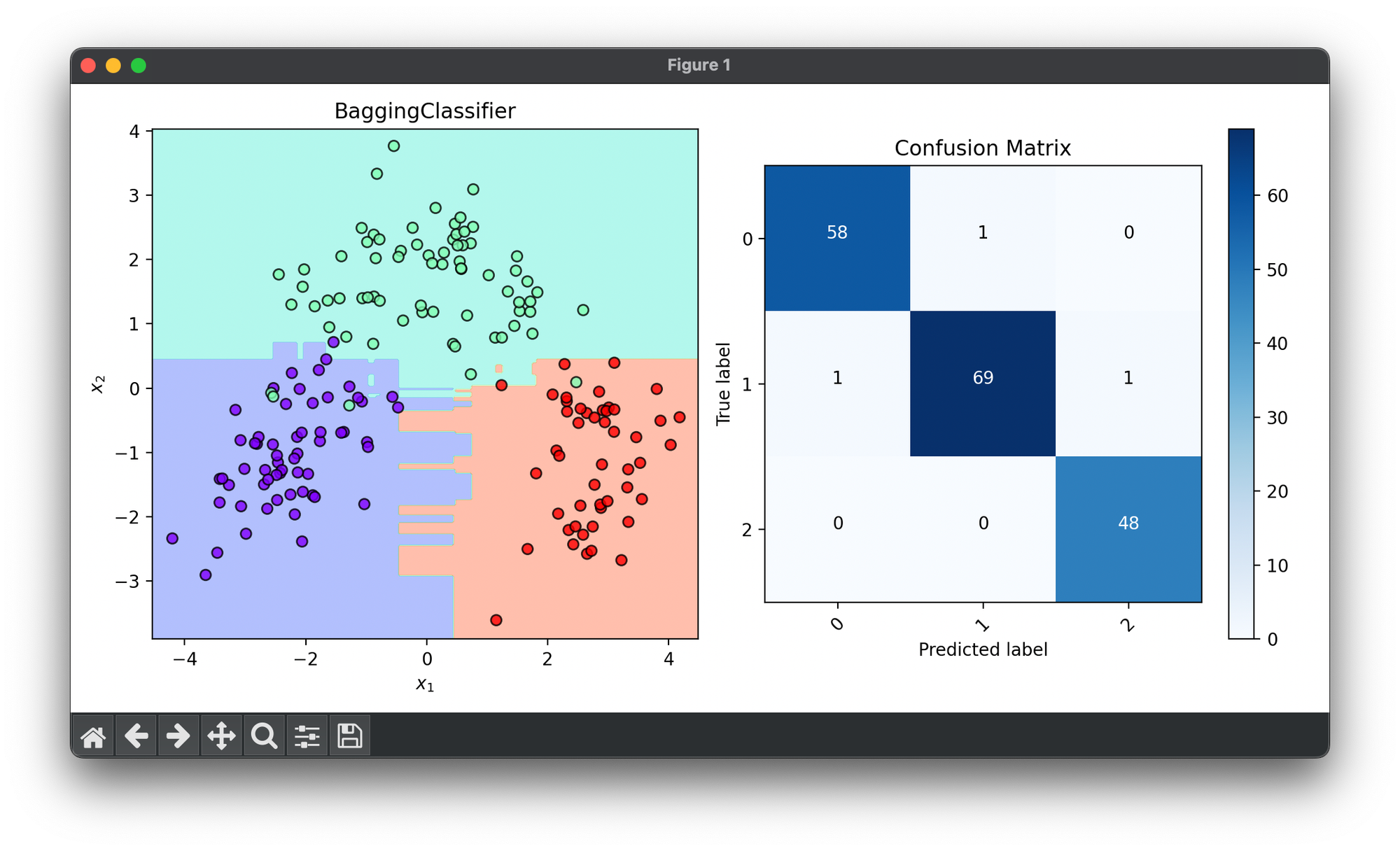

Applications

• Variance Reduction: Bagging is particularly useful for algorithms that have high variance. A common example is decision trees, where different splits in the training data can lead to very different trees.
• Classification and Regression Tasks: It can be used for both classification and regression tasks, providing a flexible tool for predictive modeling.
• Feature Selection: Bagging can be used for assessing feature importance, as the variability in the dataset can help in identifying the features that contribute most to the prediction.

Strengths and Limitations

Strengths

• Reduces Overfitting: By averaging several models, the effects of overfitting on the training data are reduced.
• Improves Model Accuracy: Combining the predictions from multiple models often results in better performance than any single model.
• Parallelizable: Since each model is built independently, the process can be parallelized to speed up training.

Limitations

• Increases Computational Complexity: Training multiple models can significantly increase the computational cost.
• Not Suitable for All Models: While bagging can improve unstable models like trees, it might not offer significant benefits for stable models like linear regression.

Advanced Topics

• Random Forests: An extension of bagging where only a subset of features is chosen at random to build each tree, leading to more diverse models.
• Bagging with Different Models: Exploring bagging with different types of base models can lead to interesting ensemble strategies, potentially improving the ensemble's performance further.

References

1. Breiman, Leo. "Bagging predictors." Machine learning 24.2 (1996): 123-140.
2. Buhlmann, Peter, and Bin Yu. "Analyzing bagging." Annals of Statistics (2002): 927-961.