Voting Regressor

Introduction

The Voting Regressor is an ensemble machine learning algorithm used for regression tasks. It combines the predictions from several different regression models to form a final prediction that, ideally, is more accurate than any individual model's prediction. This method employs the concept of ensemble learning, where the collective wisdom of multiple models is used to make predictions.

Background and Theory

Ensemble methods like the Voting Regressor are based on the principle that combining the predictions of multiple models can lead to better performance in terms of accuracy and robustness. The Voting Regressor specifically aggregates the predictions of each base regressor and then predicts the final output based on the average of these predictions. This simple yet effective method can be particularly powerful when the base regressors make independent errors, thereby canceling out each other's biases and variances to some extent.

Mathematical Foundations

Assume we have $N$ regressors $R_1, R_2,\ldots, R_N$ making predictions $y_1, y_2, \ldots, y_N$ for an input sample $x$. The final prediction $\hat{Y}$ of the Voting Regressor can be calculated as the average of these individual predictions:

where $R_i(x)$ is the prediction of the $i^\text{th}$ regressor for the sample $x$. This formula assumes equal weighting for all regressors. However, it's possible to assign different weights to each regressor if some are known to be more accurate or reliable than others.

Procedural Steps

1. Selection of Base Regressors: Choose a set of diverse regression models to include in the ensemble. Diversity can stem from using different algorithms, hyperparameters, or subsets of data.
2. Training: Each base regressor is trained independently on the training data.
3. Aggregation of Predictions:
   • Calculate the predictions from all base regressors for each input sample.
   • Compute the final prediction by averaging these individual predictions.
4. Final Prediction: Use the aggregated predictions as the final output for new input samples.

Implementation

Parameters

• estimators: List[Estimator], default = None
  List of estimators to vote
  
• weights: Vector[Scalar], default = None
  Weights for each classifier on voting
  

Examples

Test on the synthesized dataset of the curve $y=\sin(2x)\cdot\cos{e^{x/2}}+\epsilon$:

from luma.ensemble.vote import VotingRegressor
from luma.regressor.neighbors import KNNRegressor
from luma.regressor.svm import KernelSVR
from luma.regressor.tree import DecisionTreeRegressor
from luma.regressor.poly import PolynomialRegressor
from luma.regressor.linear import KernelRidgeRegressor
from luma.preprocessing.scaler import StandardScaler
from luma.metric.regression import RootMeanSquaredError

import matplotlib.pyplot as plt
import numpy as np

np.random.seed(42)

X = np.linspace(-5, 5, 500).reshape(-1, 1)
y = (np.sin(2 * X) * np.cos(np.exp(X / 2))).flatten()
y += 0.2 * np.random.randn(500)

sc = StandardScaler()
y_trans = sc.fit_transform(y)

estimators = [
    PolynomialRegressor(deg=9, alpha=0.01, regularization='l2'),
    KNNRegressor(n_neighbors=10), 
    KernelSVR(C=1.0, gamma=3.0, kernel='rbf'),
    DecisionTreeRegressor(max_depth=7, random_state=42),
    KernelRidgeRegressor(alpha=1.0, gamma=1.0, kernel='rbf')
]

vote = VotingRegressor(estimators=estimators)
vote.fit(X, y_trans)

y_pred = vote.predict(X)
score = vote.score(X, y_trans, metric=RootMeanSquaredError)

fig = plt.figure(figsize=(10, 5))
plt.scatter(X, y_trans, 
            s=10, c='black', alpha=0.3, 
            label=r'$y=\sin{2x}\cdot\cos{e^{x/2}}+\epsilon$')

for est in vote:
    est_pred = est.predict(X)
    plt.plot(X, est_pred, 
             alpha=0.5, label=f'{type(est).__name__}')
    plt.fill_between(X.flatten(), est_pred, y_pred, alpha=0.05)

plt.plot(X, y_pred, lw=2, c='blue', label='Predicted Plot')
plt.legend()
plt.xlabel('x')
plt.ylabel('y (Standardized)')
plt.title(f'VotingRegressor [RMSE: {score:.4f}]')

plt.tight_layout()
plt.show()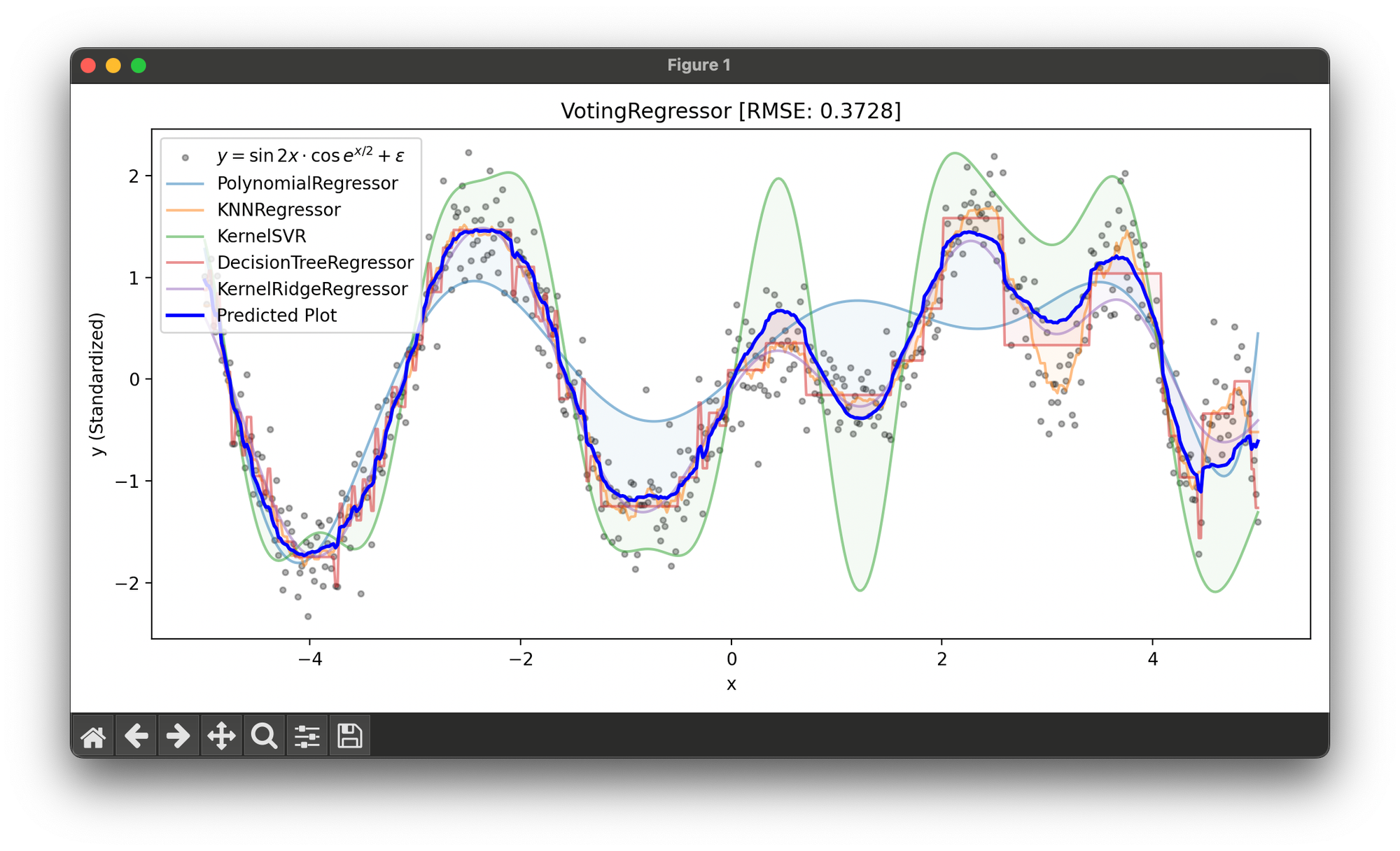

Applications

• Real Estate Valuation: Estimating property prices by combining predictions from models based on different features like location, size, and amenities.
• Financial Forecasting: Predicting stock prices, interest rates, or market trends by aggregating forecasts from a variety of financial models.
• Energy Demand Forecasting: Estimating future energy consumption by combining models trained on historical consumption data, weather patterns, and economic indicators.
• Sports Analytics: Predicting outcomes of games or performances of athletes using models based on different statistical indicators and historical performance data.

Strengths and Limitations

Strengths

• Improved Accuracy: Generally offers better prediction accuracy than any single model by leveraging their collective strengths.
• Reduced Overfitting: Ensemble methods, including the Voting Regressor, can be less prone to overfitting, especially when the base models are diverse.
• Flexibility: Can be used with any type of regression model, allowing for a wide range of combinations.

Limitations

• Complexity: Implementing and managing multiple regression models can be more complex than using a single model.
• Computation and Resource Intensity: Requires more computational resources and time, as multiple models need to be trained and maintained.
• Interpretability Issues: The final model can be more difficult to interpret than individual regressors due to the aggregation of multiple model predictions.

Advanced Topics

• Weighted Voting: Implementing weighted averaging based on the performance or reliability of each base regressor to potentially enhance the ensemble's prediction accuracy.
• Model Diversity Strategies: Techniques for selecting and combining a diverse set of base regressors to maximize the benefits of ensemble learning.
• Adaptive Voting Regressors: Dynamically adjusting the weights or selection of base regressors based on ongoing performance evaluation.

References

1. Dietterich, Thomas G. "Ensemble methods in machine learning." Multiple classifier systems. Springer, Berlin, Heidelberg, 2000.
2. Zhou, Zhi-Hua. "Ensemble methods: foundations and algorithms." Chapman and Hall/CRC, 2012.