Exponential Linear Unit (ELU)

Introduction

The Exponential Linear Unit (ELU) is a nonlinear activation function used in neural networks, introduced as a means to enhance model learning and convergence speed. ELU aims to combine the advantages of ReLU (Rectified Linear Unit) and its variants (like Leaky ReLU) while addressing their limitations, particularly the dying neuron problem and the non-zero mean output that can slow learning. By allowing negative values and smoothing the transition between negative and positive values, ELU improves neuron activation diversity and training dynamics.

Background and Theory

ReLU and Its Limitations

ReLU, defined as $f(x) = max(0, x)$, is celebrated for its simplicity and effectiveness in many deep learning tasks. However, it has two main drawbacks: neurons can "die" if they stop outputting anything other than zero, and the zero-centered output can slow down training due to imbalance in gradient flows.

Introduction to ELU

ELU aims to mitigate these issues by introducing a small twist in the negative part of its function. It is defined as:

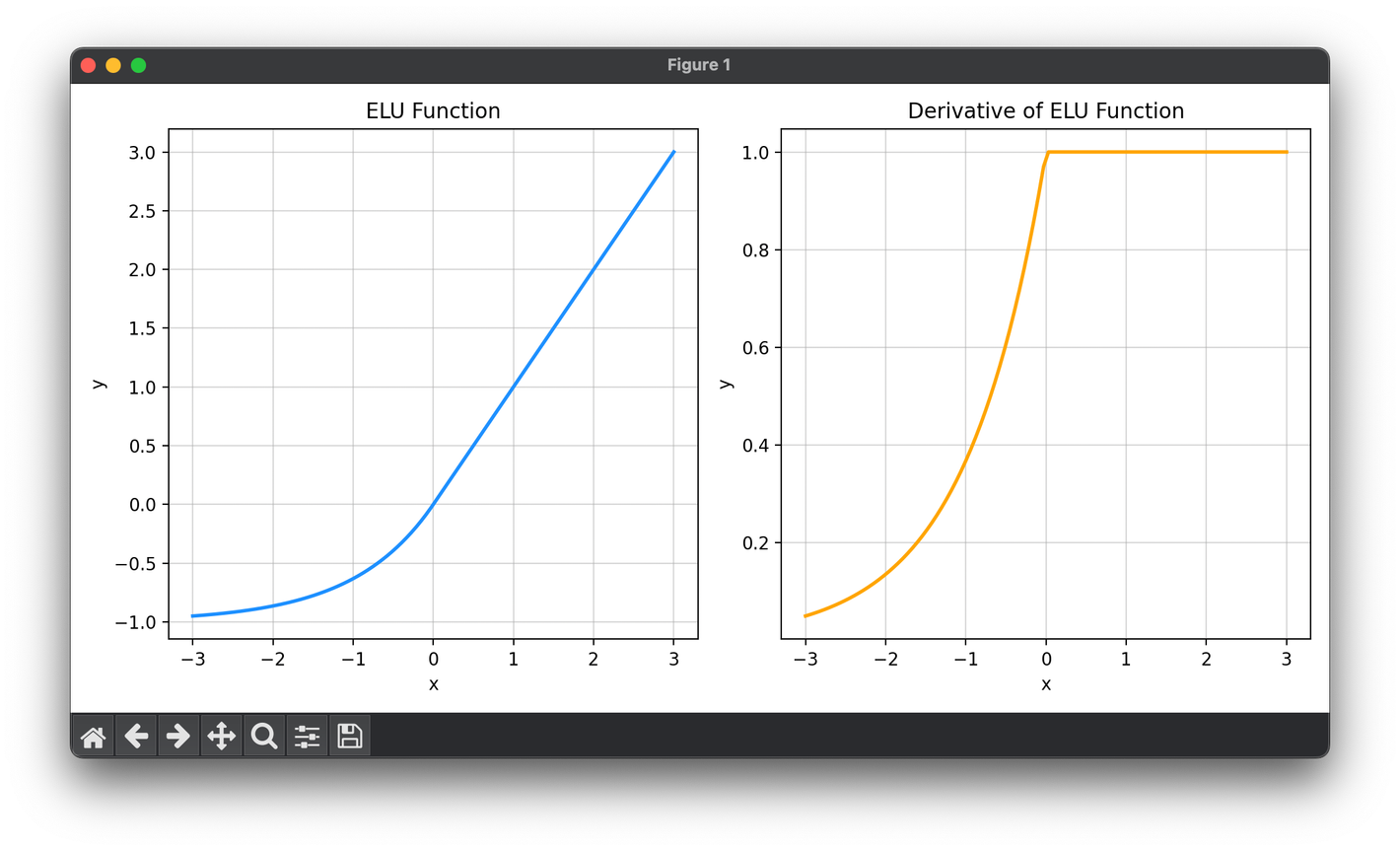
where $\alpha$ is a hyperparameter that controls the saturation level for negative inputs.

Mathematical Formulation

The key aspect of ELU is its exponential component for $x \leq 0$, which ensures:

1. Smoothness: The function is smooth everywhere, which benefits optimization and gradient flow.
2. Non-zero Gradient for Negative Inputs: Unlike ReLU, ELU allows for a non-zero gradient when $x \leq 0$, reducing the risk of dying neurons.
3. Approximate Zero Mean: The negative values of ELU, which are controlled by $\alpha$, help push the activations towards zero mean, improving the learning dynamics.

For a vector $\boldsymbol{x} = [x_1, x_2, \ldots, x_n]$, the ELU activation is calculated element-wise as:

This formulation ensures that the activation function is applied individually to each input component, maintaining the non-linear properties across the neural network layers.

Procedural Steps

The implementation of ELU in a neural network involves the following steps:

1. Initialization: Choose a value for the $\alpha$ parameter. A common default is $\alpha = 1$, but this can be adjusted based on empirical performance.
2. Forward Pass: During the network's forward pass, apply the ELU function to the input of each neuron where it is used as the activation function.
3. Backward Pass: When computing the gradients during backpropagation, use the derivative of the ELU function, which varies depending on the input value being positive or negative. The derivative is straightforward:
   • For $x > 0$, the derivative is $1$.
   • For $x \leq 0$, the derivative is $f(x) + \alpha$.

By incorporating these steps, ELU can be seamlessly integrated into the training of neural networks, offering a balance between computational efficiency and enhanced learning dynamics.

Applications

ELU has been effectively utilized across a wide range of deep learning applications, including:

• Convolutional Neural Networks (CNNs): Improving feature extraction in image recognition tasks.
• Fully Connected Networks (FCNs): Enhancing classification and regression model performance.
• Recurrent Neural Networks (RNNs): Stabilizing sequence prediction and natural language processing tasks.

Strengths and Limitations

Strengths

• Improved Learning Dynamics: By pushing mean activations closer to zero, ELU accelerates learning.
• Reduced Vanishing Gradient Problem: The non-zero gradient for negative inputs maintains active neuron state, mitigating the dying neuron issue.
• Smooth Transitions: Smoothness of the ELU function benefits optimization and model training.

Limitations

• Computational Cost: The exponential operation in ELU is more computationally intensive than ReLU and its direct variants.
• Parameter Tuning: The choice of $\alpha$ can significantly affect performance, requiring careful tuning.

Advanced Topics

Variants and Extensions

ELU has inspired several variants and extensions, aiming to further optimize activation function properties for specific applications or to introduce adaptability into the activation function's behavior.

References

1. Clevert, Djork-Arné, Thomas Unterthiner, and Sepp Hochreiter. "Fast and accurate deep network learning by exponential linear units (elus)." arXiv preprint arXiv:1511.07289 (2015).