Hyperbolic Tangent ($\tanh$)

Introduction

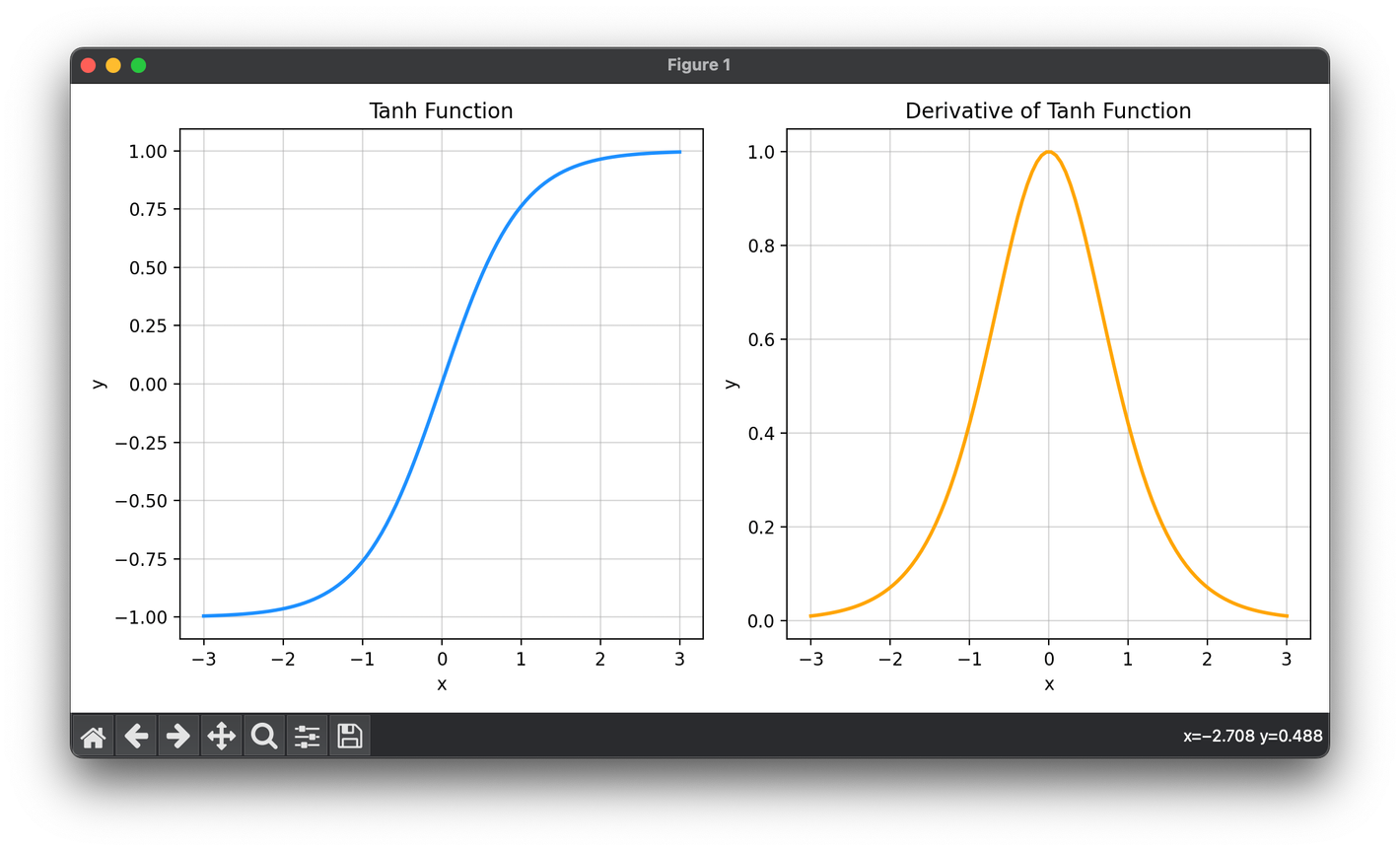
The hyperbolic tangent function, commonly referred to as tanh, is a widely used activation function in neural networks. Its mathematical form is similar to the sigmoid function but outputs values ranging from -1 to 1, making it zero-centered. This characteristic often leads to better performance in neural networks, especially in the hidden layers, by mitigating the vanishing gradient problem to some extent and helping in faster convergence.

Background and Theory

Mathematical Definition

The tanh function is defined mathematically as:

This formula showcases how tanh utilizes the exponential function to map any real-valued number to the range $[-1, 1]$. Its zero-centered nature is a significant advantage over functions like the sigmoid because it distributes the activations around 0, reducing the bias shift effect in subsequent layers.

Activation Functions in Neural Networks

Activation functions introduce non-linear properties to the network, enabling it to learn complex data patterns and perform tasks beyond mere linear classification. The choice of activation function significantly impacts the network's learning dynamics and performance.

Mathematical Formulation

The tanh function's effectiveness partly lies in its derivative, which is used during backpropagation for computing gradients:

This derivative indicates how changes in the input affect changes in the output, playing a crucial role in updating weights through gradient descent. Notably, the derivative of $\tanh$ is higher for values of $x$ closer to 0, facilitating stronger gradients and potentially faster learning, but it still suffers from the vanishing gradient problem for large values of $|x|$.

Procedural Steps

Implementing tanh as an activation function in neural networks involves:

1. Forward Pass: For each input $x$ to the neuron, the tanh function is applied to compute the output $y = \tanh(x)$. This output serves as the input to subsequent layers or the final prediction in the output layer.
2. Backward Pass: During training, the derivative of the tanh function is calculated as part of the backpropagation process to update the weights. Given an input $x$, the gradient is $1 - \tanh^2(x)$, which is used to adjust the weights in the direction that minimizes the loss.

Applications

The tanh function is particularly favored in:

• Fully Connected Layers: For hidden layers in networks where the benefits of a zero-centered activation function are pronounced.
• Recurrent Neural Networks (RNNs): Before the advent of LSTM and GRU units, tanh was extensively used in RNNs due to its properties that slightly mitigate the vanishing gradient problem, crucial for learning long-term dependencies.
• Classification and Regression Tasks: Though not typically used in the output layer for multi-class classification (where softmax is preferred), tanh is suitable for binary classification and regression problems.

Strengths and Limitations

Strengths

• Zero-Centered: Facilitates faster convergence in training due to symmetric output range.
• Mitigates Vanishing Gradient Problem: Compared to sigmoid, tanh's gradients are less likely to vanish for values of $x$ around 0.

Limitations

• Vanishing Gradient Problem: For very high or low values of $x$, the gradients tend to vanish, slowing down training or leading to the network not learning further.
• Computationally Intensive: The exponential operations make it more computationally intensive than some alternatives like ReLU.

Advanced Topics

Beyond tanh in Deep Learning

While tanh is a foundational activation function, the evolution of deep learning has seen the rise of other functions like ReLU and its variants, which, despite their simplicity, often outperform tanh in deep networks due to their ability to alleviate the vanishing gradient problem more effectively.

References

1. LeCun, Yann, Leon Bottou, Genevieve B. Orr, and Klaus-Robert Müller. "Efficient backprop." In Neural networks: Tricks of the trade, pp. 9-48. Springer, Berlin, Heidelberg, 2012.