Sigmoid

Introduction

The sigmoid activation function, also known as the logistic function, is a historically significant activation function in the field of neural networks. It maps any input value to a range between 0 and 1, making it particularly useful for models where output can be interpreted as probabilities. Despite its early popularity, the understanding of its limitations has led to the exploration and adoption of other activation functions for certain types of neural networks. However, sigmoid remains a fundamental component in the toolbox of neural network architectures, especially for binary classification tasks and the output layers of certain networks.

Background and Theory

Mathematical Definition

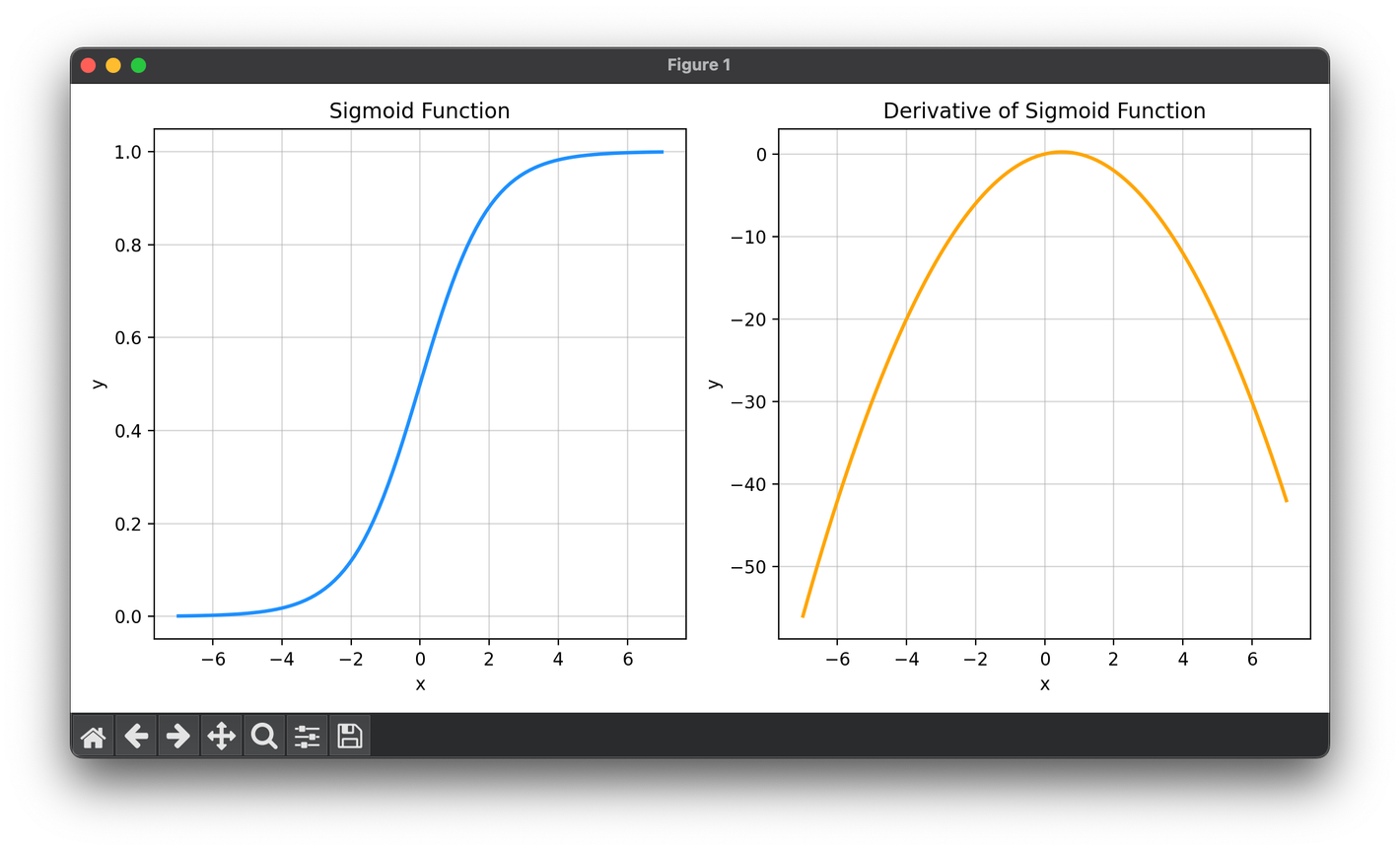
The sigmoid function is mathematically defined as:

This function asymptotically approaches 1 as $x$ becomes large and positive, and approaches 0 as $x$ becomes large and negative, with a smooth transition around $x=0$. Its "S" shaped curve is why it is often referred to as the "Sigmoid" function.

Role in Neural Networks

In neural networks, activation functions like sigmoid are used to introduce non-linearity, enabling the network to learn complex patterns beyond what is possible with linear models. The sigmoid function, in particular, has been instrumental in early neural network models and logistic regression, providing a clear probabilistic interpretation for binary classification tasks.

Mathematical Formulation

The strength of the sigmoid function in neural networks is paired with understanding its derivative, which is crucial for the backpropagation algorithm used in training neural networks. The derivative of the sigmoid function, with respect to its input $x$, is:

This expression shows that the gradient of the sigmoid function depends on the output value itself, making it computationally efficient to calculate during the optimization process.

Procedural Steps

Implementing the sigmoid function within a neural network involves two primary steps:

1. Forward Pass: For each neuron input $x$, apply the sigmoid function to calculate the output $y = \sigma(x)$. This output can be used directly for binary classification or fed into subsequent layers in a deeper network.
2. Backward Pass: During the training phase, the derivative of the sigmoid function is computed as part of the gradient descent process to update the network's weights. The gradient, given by $\sigma^\prime(x)$, is multiplied by the gradient of the loss function with respect to the output, propagating the error backward through the network.

Applications

• Binary Classification: Ideal for the output layer in binary classification, where the output can be interpreted as the probability of the positive class.
• Neural Network Gates: Used in the gating mechanisms of certain RNN architectures, such as LSTM and GRU cells, to control the flow of information.
• Probabilistic Models: In models where outputs are probabilities, the sigmoid function ensures that the outputs remain within the $[0, 1]$ range.

Strengths and Limitations

Strengths

• Output Interpretability: Outputs can be directly interpreted as probabilities, offering a clear probabilistic understanding.
• Smooth Gradient: The smooth nature of the sigmoid function facilitates gradient-based optimization methods.

Limitations

• Vanishing Gradient Problem: For inputs with large magnitude (both positive and negative), the sigmoid function saturates, leading to gradients close to zero. This significantly slows down the learning process or even stops it entirely, as gradients propagated back through the network become negligible.
• Not Zero-Centered: Since the output is always positive, gradient updates can consistently be all positive or all negative, leading to zig-zagging dynamics during optimization.

Advanced Topics

Alternatives to Sigmoid

The recognition of sigmoid's limitations has led to the exploration and adoption of other activation functions designed to mitigate these issues, such as ReLU (Rectified Linear Unit) and its variants, which are now more commonly used in hidden layers of deep neural networks due to their ability to alleviate the vanishing gradient problem and speed up training.

References

1. Han, Jun, and Claudio Moraga. "The influence of the sigmoid function parameters on the speed of backpropagation learning." In From Natural to Artificial Neural Computation, pp. 195-201. Springer, Berlin, Heidelberg, 1995.