Momentum Optimization

Introduction

The Momentum Optimizer is an advanced variant of the classical stochastic gradient descent (SGD) algorithm, designed to accelerate the convergence of gradient-based optimization algorithms by incorporating the concept of momentum. This technique simulates the inertia of an object in motion, effectively allowing the optimizer to continue moving in the direction of the gradient over multiple iterations, thus reducing oscillations and speeding up convergence, especially in landscapes with steep ravines or flat plateaus.

Background and Theory

In classical SGD, parameters are updated solely based on the current gradient, which can lead to slow convergence or oscillation in the parameter space. The Momentum Optimizer addresses these issues by adding a fraction of the previous parameter update vector to the current update. This approach draws inspiration from physics, where the momentum of an object is the product of its mass and velocity, allowing it to overcome obstacles and move through less optimal areas more quickly.

Mathematically, the momentum update rule introduces a velocity vector $v$, which accumulates the gradient of the loss function $L$ with respect to the parameters $\theta$ over iterations. The parameters are then updated not only based on the current gradient but also on the accumulated past gradients. The update rule for the parameters using Momentum Optimizer can be expressed as follows:

where:

• $v_{t}$ is the velocity at time step $t$,
• $\gamma$ is the momentum coefficient (typically set between 0.9 and 0.99),
• $\eta$ is the learning rate, and
• $\nabla_\theta L(\theta)$ is the gradient of the loss function with respect to $\theta$ at the current step.

Procedural Steps

1. Initialization: Initialize the parameters $\theta$ of the model and the velocity vector $v$ to zeros.
2. Gradient Computation: Compute the gradient of the loss function $\nabla_\theta L(\theta)$ with respect to the parameters for the current mini-batch.
3. Velocity Update: Update the velocity vector $v$ by blending the current gradient with the previous velocity, scaled by the momentum coefficient $\gamma$.
4. Parameter Update: Update the parameters $\theta$ by subtracting the current velocity vector $v$.
5. Repeat: Repeat steps 2-4 until the convergence criteria are met or a predefined number of iterations is reached.

Mathematical Formulation

The momentum term $\gamma v_{t-1}$ effectively adds a fraction of the previous update to the current update, thereby 'smoothing out' the updates and preventing erratic movements in parameter space. This can be particularly beneficial in scenarios where the gradient may be noisy or the loss landscape has poor conditioning (e.g., steep valleys).

The update equations can be rewritten in a more detailed form as:

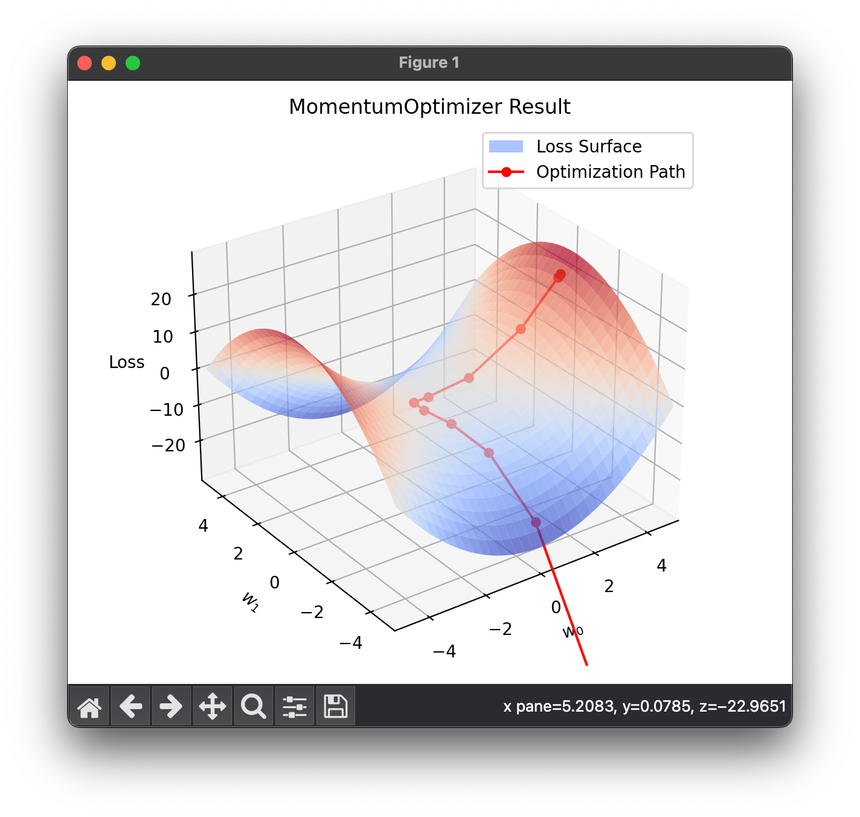
This formulation demonstrates how the momentum optimizer navigates the parameter space more effectively by considering the history of gradients.

Applications

The Momentum Optimizer is widely used in training deep neural networks, where it has been shown to improve convergence rates and achieve better performance on various tasks, including image classification, natural language processing, and reinforcement learning.

Strengths and Limitations

Strengths

• Faster Convergence: By accumulating a history of gradients, momentum often leads to faster convergence than classical SGD.
• Reduced Oscillation: Momentum helps dampen oscillations in directions of high curvature, providing smoother convergence.

Limitations

• Hyperparameter Sensitivity: The performance of the momentum optimizer can be sensitive to the choice of the momentum coefficient $\gamma$ and the learning rate $\eta$.
• No Guarantee of Optimal Convergence: While momentum can speed up convergence, it does not guarantee that the convergence will be to a global minimum or a better local minimum.

Advanced Topics

• Nesterov Accelerated Gradient (NAG): An extension of the momentum optimizer that calculates the gradient at the anticipated position of the parameters, providing a more accurate direction for the updates.
• Adaptation in Learning Rates: Integrating momentum with adaptive learning rate algorithms like Adam for even more robust optimization strategies.

References

1. Qian, Ning. "On the momentum term in gradient descent learning algorithms." Neural networks 12.1 (1999): 145-151.
2. Sutskever, Ilya, et al. "On the importance of initialization and momentum in deep learning." Proceedings of the 30th international conference on machine learning (ICML-13). 2013.