Locally Tangent Space Alignment (LTSA)

Introduction

Locally Tangent Space Alignment (LTSA) is a prominent technique in the realm of non-linear dimensionality reduction, focusing on preserving the local geometry of high-dimensional data by aligning local tangent spaces. Introduced by Zhenyue Zhang and Hongyuan Zha in their influential work, LTSA stands out for its mathematical elegance and practical effectiveness in capturing the intrinsic geometry of data manifolds. This document delves into LTSA, emphasizing its mathematical foundations, procedural steps, and practical implications, closely adhering to the original authors' explanations.

Background and Theory

LTSA is predicated on the manifold assumption, which posits that high-dimensional data points often reside on a lower-dimensional manifold embedded within the high-dimensional space. Unlike global linear approaches, LTSA aims to uncover this manifold by exploring the data's local linear structures, subsequently aligning these local views to reveal the manifold's global structure.

Key Concepts

• Manifold Learning: The process of identifying and leveraging the lower-dimensional structures (manifolds) within high-dimensional data.
• Tangent Space: A tangent space at a point on the manifold is a linear space that best approximates the manifold around that point.
• Local Linear Approximation: Assuming each data point and its neighbors lie approximately on a linear patch of the manifold, resembling its local tangent space.

Mathematical Formulation

The LTSA algorithm can be broken down into several mathematical steps, which we'll explore in detail:

Local Tangent Space Estimation

Given a high-dimensional dataset $\{x_i\}_{i=1}^N$ where each $x_i \in \mathbb{R}^D$, the aim is to find a lower-dimensional representation $\{y_i\}_{i=1}^N$ where each $y_i \in \mathbb{R}^d$ and $d < D$. For each point $x_i$, identify its $k$ nearest neighbors and construct the local covariance matrix:

where $X_i$ is the matrix of neighbors of $x_i$ and $\bar{X}_i$ is the mean-centered matrix of $X_i$. The local tangent space is then approximated by the leading $d$ eigenvectors $T_i$ of $C_i$, corresponding to the $d$ largest eigenvalues.

Local Coordinates in Tangent Spaces

For each point $x_i$ and its neighbors, project the neighbors onto the tangent space $T_i$ to obtain local coordinates $Z_i$:

where $\bar{x}_i$ is the mean of the neighbors of $x_i$.

Alignment of Local Tangent Spaces

The core of LTSA lies in aligning these local tangent spaces to construct a global coordinate system. This involves minimizing the discrepancy between local coordinates $Z_i$ in their respective tangent spaces and their corresponding coordinates in the global space. Formally, we seek to minimize:

where $Y$ is the matrix of low-dimensional embeddings for all points, $B_i$ is a matrix that maps global coordinates to local coordinates for the neighborhood of point $i$, and $\|\cdot\|_F$ denotes the Frobenius norm.

4. Constructing the Embedding

The solution to the optimization problem is found by constructing a matrix $L$ from the local contributions of each point and its neighbors and then solving an eigenvalue problem. Specifically, the matrix $L$ is defined such that $L = BB^T$, where $B$ is constructed from all $B_i$. The lower-dimensional embeddings $Y$ are then given by the eigenvectors corresponding to the $d$ smallest non-zero eigenvalues of $L$.

Procedural Steps

1. Neighborhood Selection: For each data point, select $k$ nearest neighbors.
2. Local Tangent Space Estimation: Estimate the tangent space for each point using PCA on its neighbors.
3. Local Coordinates Computation: Project the neighbors onto the local tangent spaces to obtain local coordinates.
4. Alignment of Local Tangent Spaces: Align all local tangent spaces to find a consistent global embedding by minimizing the discrepancy between local and global representations.
5. Global Coordinates Construction: Solve the eigenvalue problem to find the global low-dimensional embedding that best aligns the local tangent spaces.

Implementation

Parameters

• n_components: int
  Dimensionality of low-space
  
• n_neighbors: int, default = 10
  Number of neighbors to construct a local tangent space
  

Examples

Test on the Swiss roll dataset:

from luma.reduction.manifold import LTSA

from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt

X, y = make_swiss_roll(n_samples=500, noise=0.2)

model = LTSA(n_components=2, n_neighbors=8)
Z = model.fit_transform(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1, projection="3d")
ax2 = fig.add_subplot(1, 2, 2)

ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap="rainbow")
ax1.set_xlabel(r"$x$")
ax1.set_ylabel(r"$y$")
ax1.set_zlabel(r"$z$")
ax1.set_title("Original Swiss-Roll")

ax2.scatter(Z[:, 0], Z[:, 1], c=y, cmap="rainbow")
ax2.set_xlabel(r"$z_1$")
ax2.set_ylabel(r"$z_2$")
ax2.set_title(f"After {type(model).__name__}")
ax2.grid(alpha=0.2)

plt.tight_layout()
plt.show()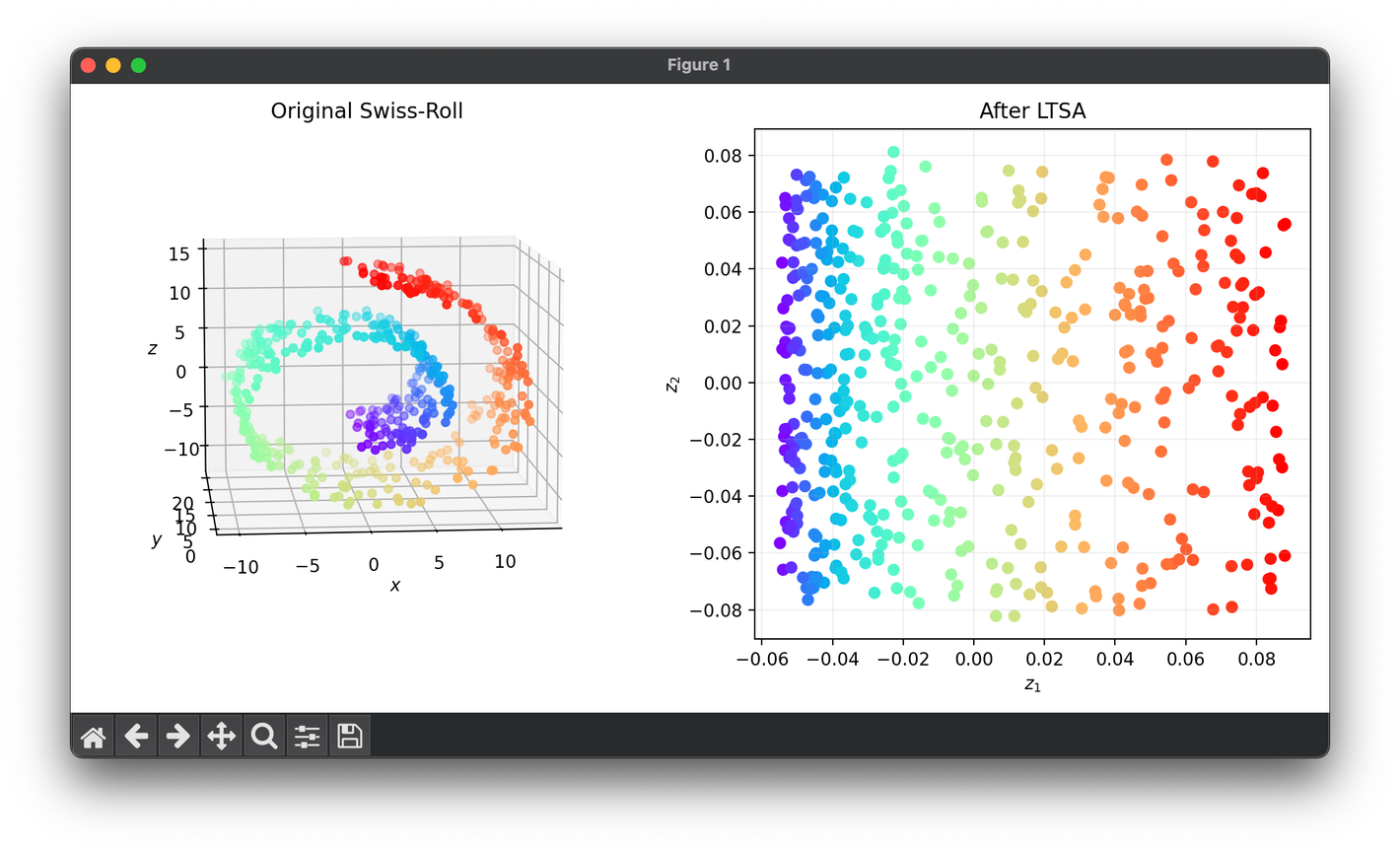

Applications

LTSA is widely applied in areas such as:

• Image processing and computer vision for feature extraction and recognition.
• Bioinformatics for gene expression data analysis.
• Speech recognition where capturing the underlying structure of sound data is crucial.

Strengths and Limitations

Strengths

• Local Geometry Preservation: Effectively captures the local geometric structures of the data.
• Robustness to Noise: Performs well even in the presence of noise due to the local nature of the algorithm.

Limitations

• Parameter Sensitivity: The choice of $k$ for neighborhood size can significantly impact the outcome.
• Non-convex Optimization: The alignment step involves solving a non-convex optimization problem, which may not always converge to the global optimum.

Advanced Topics

• Scalability Improvements: Research into making LTSA more scalable for large datasets through algorithmic optimizations.
• Integration with Other Techniques: Combining LTSA with other dimensionality reduction or machine learning techniques for enhanced data analysis capabilities.

References

1. Zhang, Zhenyue, and Hongyuan Zha. "Principal Manifolds and Nonlinear Dimension Reduction via Tangent Space Alignment." Journal of Shanghai University (English Edition), 2004.